1. Момент инерции. Теорема Штейнера.

Момент инерции определяется как , если распределение массы равномерно, то заменяется на – элементарный объём, – плотность вещества. .

Теорема Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тала на квадрат расстояния а между осями: .

Момент инерции:

1. однородного тонкого стержня массы , длины относительно оси, проходящей через центр масс и перпендикулярной стержню:

2. однородного тонкого стержня массы , длины относительно оси, проходящей через один из концов стержня:

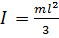
3. тонкого кольца массы , радиуса R относительно оси симметрии, перпендикулярной плоскости кольца:

4. однородного диска (цилиндра) массы , радиуса R, высоты h относительно оси симметрии, перпендикулярной основанию: .

Тензор инерции — в механике абсолютно твёрдого тела — тензорная величина, связывающая момент импульса тела и кинетическую энергию его вращения с его угловой скоростью: где — тензор инерции, — угловая скорость, — момент импульса Используя, например, определение момента импульса системы N материальных точек (перенумерованных в формулах ниже индексом k):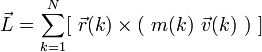

и кинематическое выражение для скорости через угловую скорость:

и сравнивая с формулой, выражающей момент импульса через тензор инерции и угловую скорость (первой в этой статье), нетрудно получить явное выражение для тензора инерции: или в непрерывном виде: , где r — расстояния от точек до центра, относительно которого вычисляется тензор инерции, а ri — координатные компоненты соответствующих отрезков, i и j — номера координат (от 1 до 3), индекс же k (от 1 до N) в дискретной формуле нумерует точки системы или маленькие части, её составляющие. Уже из этих формул явно видно, что тензор инерции любого тела зависит от точки, относительно которой он рассчитан. Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:

где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm. Ось OX называется главной осью инерции тела, если центробежные моменты инерции J_xy и J_xz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела. Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси: где: m_i — масса i-й точки, r_i — расстояние от i-й точки до оси. Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

,где: — масса малого элемента объёма тела , — плотность, — расстояние от элемента до оси a. Если тело однородно, то есть его плотность всюду одинакова, то

Гироскоп (или волчок) – массивное твёрдое тело, симметричное некоторой оси, совершающее вращения вокруг неё с большой угловой скоростью. В силу симметрии гироскопа выполняется . При попытке повернуть вращающийся гироскоп вокруг некоторой оси наблюдается гироскопический эффект – под действием сил, которые, казалось бы, должны были вызвать поворот оси гироскопа ОО вокруг прямой О’O’, ось гироскопа поворачивается вокруг прямой О’’О’’ (ось ОО и прямая О’O’ предполагаются лежащими в плоскости чертежа, а прямая О’’О’’ и силы f1 и f2 – перпендикулярными к этой плоскости). Объяснение эффекта основано на использование уравнения момента . Момент импульса поворачивается вокруг оси ОХ в силу соотношения . Вместе с вокруг ОХ поворачивается и гироскоп. Вследствие гироскопического эффекта на подшипнике, на котором вращается гироскоп, начинают действовать гироскопические силы. Под действием гироскопических сил ось гироскопа стремиться занять положение, параллельное угловой скорости вращения Земли.

Описанное поведение гироскопа положено в основу гироскопического компаса. Преимущества гироскопа: указывает точное направление на географический северный полюс, его работа не подвержена воздействию металлических предметов.

Прецессия гироскопа – особый вид движения гироскопа имеет место в том случае, если момент действующих на гироскоп внешних сил, оставаясь постоянным по величине, поворачивается одновременно с осью гироскопа, образуя с ней всё время прямой угол. Рассмотрим движение гироскопа с одной закреплённой точкой на оси под действием силы тяжести , – расстояние от закреплённой точки до центра инерции гироскопа, – угол между гироскопом и вертикалью. направлен момент перпендикулярно к вертикальной плоскости, проходящей через ось гироскопа. Уравнение движения: приращение импульса = Следовательно, изменяет своё положение в пространстве таким образом, что его конец описывает окружность в горизонтальной плоскости. За промежуток времени гироскоп повернулся на угол ось гироскопа описывает конус вокруг вертикальной оси с угловой скоростью – угловая скорость прецессии.

П лоскопаралле́льное движе́ние (плоское движение) — вид движения абсолютно твёрдого тела, при котором все точки тела совершают движение параллельно некоторой плоскости. Примером плоскопараллельного движения является качение колеса по горизонтальной дороге . Уравнения плоского движения: xA= f1(t), yA= f2(t), j = f3(t), точка А назыв. полюсом. Плоское движение тв.тела слагается из поступательного движения, при котором все точки тела движутся так же, как полюс (А),и из вращательного движения вокруг этого полюса. Поступательное перемещение зависит от выбора полюса, а величина и направление угла поворота не зависят. Скорости точек тела при плоском движении: ; , v_BA= w×BA, т.е. скорость какой-либо точки В плоской фигуры равна геометрической сумме скорости полюса А и скорости точки В при вращении плоской фигуры вокруг полюса А. Теорема: при плоском движении проекции скоростей двух точек тела на ось, проходящую через эти точки, равны между собой: v_Acosa = v_Bcosb. Теорема Шаля: плоскую фигуру можно переместить из одного положения в любое другое положение на плоскости одним поворотом этой фигуры вокруг некоторого неподвижного центра. Этот центр на неподвижной плоскости, совпадает с м.ц.с. и называется мгновенным центром вращений (ось вращений). При движении плоской фигуры м.ц.с. непрерывно изменяет свое положение. Геометрическое место м.ц.с., отмеченных на неподвижной плоскости, называется неподвижной центроидой. Геометрическое место м.ц.с., отмеченных на плоскости фигуры, назыв. подвижной центроидой (колесо катится по прямой: неподвижная центроида – прямая, подвижная – окружность). При движении плоской фигуры подвижная центроида катится без скольжения по неподвижной центроиде (теорема Пуансо).

Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением. Основные кинематические характеристики вращательного движения тела — его угловая скорость ( ) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:

и кинетическая энергия , где I_z — момент инерции тела относительно оси вращения. Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I₁, I₂ и I₃. Вращательная энергия такой молекулы задана выражением

где ω₁, ω₂, и ω₃ — главные компоненты угловой скорости. В общем случае, энергия при вращении с угловой скоростью находится по формуле: , где — тензор инерции.

Кинетическая энергия вращающегося тела и работа внешних сил (ось вращения неподвижна). Скорость i -й частицы тела где - расстояние частицы до оси вращение Кинетическая энергия

так как угловая скорость вращения для всех точек одинакова. В соответствии с законом изменения механической энергии системы элементарная работа всех внешних сил равна приращению кинетической энергии тела:

Работа внешних сил при повороте тела на конечный угол равна Допустим, что диск точила вращается по инерции с угловое скоростью и мы останавливаем его, прижимая какой-либо предмет к краю диска с постоянным усилием. При этом на диск будет действовать постоянная по величине сила направленная перпендикулярно его оси. Работа этой силы

где - радиус диска, - угол его поворота. Число оборотов, которое сделает диск до полной остановки,

где - момент инерции диска точила вместе с якорем электромотора.

Колебания – процессы, характеризующиеся той или иной степенью повторяемости по времени. В зависимости от физической природы повторяющегося процесса различают колебания: механические, электромагнитные, электромеханические и другие. Все эти процессы, несмотря на различную физическую природу, описываются одинаковыми математическими уравнениями и имеют ряд общих свойств. Механические колебания – это повторяющееся движение, при котором тело многократно проходит одно и то же положение в пространстве. Различают периодические и непериодические колебания. Периодическими называют колебания, при которых координата и другие характеристики тела описываются периодическими функциями времени. Гармоническое колебание — явление периодического изменения какой-либо величины, при котором зависимость от аргумента имеет характер функции синуса или косинуса. Например, гармонически колеблется величина, изменяющаяся во времени следующим образом:

или , где х — значение изменяющейся величины, t — время, остальные параметры — постоянные: А — амплитуда колебаний, ω — циклическая частота колебаний, — полная фаза колебаний, — начальная фаза колебаний. Обобщенное гармоническое колебание в дифференциальном виде

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Чтобы свободные колебания были гармоническими, необходимо, чтобы колебательная система была линейной (описывалась линейными уравнениями движения), и в ней отсутствовала диссипация энергии (последняя вызвала бы затухание). Вынужденные колебания совершаются под воздействием внешней периодической силы. Чтобы они были гармоническими, достаточно чтобы колебательная система была линейной (описывалась линейными уравнениями движения), а внешняя сила сама менялась со временем как гармоническое колебание (то есть чтобы зависимость от времени этой силы была синусоидальной).

Гармонический осциллятор (в классической механике) — это система, которая при смещении из положения равновесия испытывает действие возвращающей силы , пропорциональной смещению (согласно закону Гука): , где — коэффициент жёсткости системы.

Если — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.

Уравнение движения гармонического осциллятора и его общее решение

В качестве модели консервативного гармонического осциллятора возьмём груз массы , закреплённый на пружине жёсткостью .Пусть — это смещение груза относительно положения равновесия. Тогда, согласно закону Гука, на него будет действовать возвращающая сила: Используя второй закон Ньютона, запишем Обозначая и заменяя ускорение на вторую производную от координаты по времени , напишем: Это дифференциальное уравнение описывает поведение консервативного гармонического осциллятора. Коэффициент называют циклической частотой осциллятора. (Здесь имеется в виду круговая частота, измеряющаяся в радианах в секунду. Чтобы перевести её в частоту, выражающуюся в Герцах, надо разделить круговую частоту на ) Будем искать решение этого уравнения в виде: Здесь —амплитуда (максимальное значение смещения или изменения переменной величины от среднего значения при колебательном или волновом движении), — частота колебаний (пока не обязательно равная собственной частоте), — начальная фаза. Подставляем в дифференциальное уравнение.

И остаётся условие на частоту колебаний:

Отрицательную частоту можно отбросить, так как произвол в выборе этого знака покрывается произволом выбора начальной фазы. Общее решение уравнения записывается в виде: ,где амплитуда и начальная фаза — произвольные постоянные. Эта запись исчерпывает все решения дифференциального уравнения, так как позволяет удовлетворить любым начальным условиям (начальному положению груза и его начальной скорости). Итого, консервативный гармонический осциллятор может совершать чисто гармонические колебания с частотой, равной его собственной частоте, с амплитудой любой величины и с произвольной начальной фазой. Кинетическая энергия записывается в виде .

и потенциальная энергия есть тогда полная энергия имеет постоянное значение

Фа́за колеба́ний — физическая величина, меняющаяся со временем, при заданной амплитуде определяющая состояние колебательной системы в (любой) данный момент времени. Период колеба́ний — наименьший промежуток времени, за который осциллятор совершает одно полное колебание. Частота колебаний — число колебаний в единицу времени.

Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела. Определения

• — угол отклонения маятника от равновесия; — начальный угол отклонения маятника; — масса маятника; — расстояние от точки подвеса до центра тяжести маятника; — радиус инерции относительно оси, проходящей через центр тяжести.

• — ускорение свободного падения. Момент инерции относительно оси, проходящей через точку подвеса: .

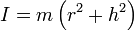Дифференциальное уравнение движения физического маятника

Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:

Полагая , предыдущее уравнение можно переписать в виде:

Последнее уравнение аналогично уравнению колебаний математического маятника длиной . Величина называется приведённой длиной физического маятника.

Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.

Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии от точки подвеса. Эта точка и будет центром качания маятника. Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен , а момент силы тяжести относительно той же оси . Легко заметить, что уравнение движения не изменится.

Теорема Гюйгенса

Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.

Доказательство Вычислим приведенную длину для нового маятника:

Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.

Период малых колебаний физического маятника Если амплитуда колебаний мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:

Эта формула даёт результаты приемлемой точности (ошибка менее 1 %) при углах, не превышающих 4°.Следующий порядок приближения можно использовать с приемлемой точностью (ошибка менее 1 %) при углах до 1 радиана (≈60°) .

Свободные затухающие колебания – колебания, у которых амплитуды из-за потерь энергии колебательной системой с течением времени убывают. Простейшим механизмом убывания энергии колебаний есть ее превращение в теплоту вследствие трения в механических колебательных системах, а также потерь, связанных с выделением теплоты, и излучения электромагнитной энергии в электрических колебательных системах.

Вид закономерностей затухания колебаний задается свойствами колебательных систем. Обычно рассматривают линейные системы — идеализированные реальные системы, параметры которых, определяющие физические свойства системы, в ходе процесса остаются неизменными. Например, линейными системами являются пружинный маятник при малых растяжениях пружины (когда выполняется закон Гука), колебательный контур, у которого сопротивление, индуктивность и емкость не зависят ни от тока в контуре, ни от напряжения. Различные по своей природе линейные системы описываются аналогичными линейными дифференциальными уравнениями, что дает основания подходить к изучению колебаний различной физической природы с единой точки зрения, а также моделировать их, в том числе и на ЭВМ.

Дифференциальное уравнение свободных затухающих колебаний линейной системы определяется как

(1) , где s – колеблющаяся величина, которая описывает тот или иной физический процесс, δ = const — коэффициент затухания, ω₀ - циклическая частота свободных незатухающих колебаний той же колебательной системы, т. е. при δ=0 (при отсутствии потерь энергии) называется собственной частотой колебательной системы.

Решение уравнения (1) запишем в виде

(2)

где u=u(t). После взятия первой и второй производных (2) и подстановки их в выражение (1) найдем

(3)

Решение уравнения (3) зависит от знака коэффициента перед искомой величиной. Рассмотрим случай положительного коэффициента: (4)

(если (ω02 - σ2)>0, то такое обозначение мы вправе сделать). Тогда получим выражение , у которого решение будет функция . Значит, решение уравнения (1) в случае малых затуханий (ω02 >> σ2 )

(5)

где (6)

— амплитуда затухающих колебаний, а А₀ — начальная амплитуда.

(5)

где (6) — амплитуда затухающих колебаний

Затухание не дает колебаниям быть периодичными и, строго говоря, к ним нельзя применять понятие периода или частоты. Но если затухание мало, то можно условно использовать понятие периода как промежутка времени между двумя последующими максимумами (или минимумами) колеблющейся физической величины . В этом случае период затухающих колебаний с учетом выражения (4) будет равен

Если A(t) и А(t + Т) — амплитуды двух последовательных колебаний, соответствующих моментам времени, которые отличаются на период, то отношение

называется декрементом затухания, а его логарифм

(7)

— логарифмическим декрементом затухания; N_e — число колебаний, которые совершаются за время уменьшения амплитуды в е раз. Логарифмический декремент затухания является постоянной величиной для данной колебательной системы.

Для характеристики колебательной системы также применяют понятие добротности Q, которая при малых значениях логарифмического декремента будет равна

(8)

(так как затухание мало (ω₀² >> σ² ), то T принято равным Т₀).

Из формулы (8) вытекает, что добротность пропорциональна числу колебаний Ne, которые система совершает за время релаксации.

Выводы и уравнения, полученные для свободных затухающих колебаний линейных систем, можно использовать для колебаний различной физической природы — механических (в качестве примера возьмем пружинный маятник) и электромагнитных (в качестве примера возьмем электрический колебательный контур).

Вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы (вынуждающая сила).