Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел. Материа́льная то́чка— простейшая физическая модель в механике — тело, размеры которого допустимо считать бесконечно малыми в пределах допущений исследуемой задачи. Практически под материальной точкой понимают обладающее массой тело, размерами и формой которого можно пренебречь при решении данной задачи. Кинематический закон движения – это функция, выражающая положение точки в любой момент времени: r = r(t) (Изменение радиус-вектора с течением времени) Уравнение является векторной формой закона. Движение материальной точки полностью определено, если координаты материальной точки заданы в зависимости от времени: x = x(t), y = y(t), z = z(t) . Вектор перемещения ∆r = r - r₀ – это вектор, проведенный из начального положения движущейся точки в положение ее в данный момент времени (приращение радиус-вектора точки за рассматриваемый промежуток времени): ∆r = r - r₀ = r(t) - r(t₀) . В пределе ∆t→0 модуль элементарного перемещения равен элементарному пути: |dr| = ds . Скорость – векторная величина, значит, её можно записать в виде . С другой стороны . Следовательно, проекция скорости … Величина (модуль) скорости . При движении материальной точки её скорость меняется как по величине, так и по направлению. Как быстро это происходит в произвольный момент времени, характеризует векторная величина ускорение. . Проекция вектора ускорения Траектория – это кривая, которую описывает радиус-вектор r(t) координат материальной точки (или тела) с течением времени. Пройденный путь частицы от до . Угловая скорость и угловое ускорение. Связь между угловыми и линейными величинами. Поворот абсолютно твёрдого тела на угол вокруг некоторой оси можно задать с помощью направляющего отрезка . – длина этого отрезка совпадает с углом поворота, а направление параллельно оси вращения и определяется правилом правого винта. Для не выполняется правило сложения векторов. однако при бесконечно малых (элементарных) поворотах правило сложения векторов выполняется. Как быстро происходит вращение характеризует векторная (псевдовекторная) величина угловая скорость . При равномерном движении вокруг неподвижной оси величина угловой скорости . Естественным образом обобщена на случай вращения с переменной понятие количества оборотов, или частота вращения ( , ) и период ( , ). При произвольном вращении угловая скорость может меняться как по величине, так и по направлению. Для характеристики такого измерения вводится псевдовектор углового ускорения . При вращении тела вокруг неподвижной оси все его точки движутся по окружности, скорости и ускорения различных точек различны, а угловые скорости и ускорения одинаковы. Угол, измеряемый в радианах , l – длина дуги, на которую опирается угол, . Точка движется по окружности, поэтому у неё есть нормальное ускорение ( ) и тангенциальное ( ).

.

Ускорение. Нормальное и тангенциальное ускорения

При движении материальной точки её скорость меняется как по величине, так и по направлению. Как быстро это происходит в произвольный момент времени, характеризует векторная величина ускорение. . Проекция вектора ускорения …

Рассмотрим движение частицы, совершаемое в плоскости. Скорость направлена по касательной траектории, поэтому можно записать . Здесь единичный вектор задаёт направление касательной, .

Ускорение , направленное по касательной к траектории, определяемое скоростью изменение величины скорости, или модуля, называется тангенциальным ускорением.

– нормальное ускорение (характеризует быстроту изменения направления скорости), - единичный вектор, перпендикулярный и направленный внутрь кривой, R – радиус кривизны линии.

Разложение ускорения на тангенциальную и нормальную компоненты (вторая из которых и есть центростремительное или нормальное ускорение) можно найти, продифференцировав по времени вектор скорости, представленнный в виде через единичный вектор касательной :

где первое слагаемое — тангенциальное ускорение, а второе — нормальное ускорение.

Здесь использовано обозначение для единичного вектора нормали к траектории и — для текущей длины траектории ( ); в последнем переходе также использовано очевидное . Далее можно просто формально назвать член — нормальным (центростремительным) ускорением. При этом его смысл, смысл входящих в него объектов, а также доказательство того факта, что он действительно ортогонален касательному вектору (то есть что — действительно вектор нормали) — будет следовать из геометрических соображений (впрочем, то, что производная любого вектора постоянной длины по времени перпендикулярна самому этому вектору, — достаточно простой факт; в данном случае мы применяем это утверждение для ).

Равнопеременное движение - движение точки, при котором её касательное ускорение w_t (в случае прямолинейного Р. д. всё ускорение w) постоянно. Скорость v, которую имеет точка через t сек после начала движения, и её расстояние s от начального положения, измеренное вдоль дуги траектории, определяются при Р. д. равенствами: v = v₀ + w_tt, s = v₀t + w_tt²/2, где v₀ — начальная скорость точки. Когда знаки v и w_t одинаковы, Р. д. является ускоренным, а когда разные — замедленным. Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Зная, что , найдём формулу для определения координаты x:

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается. В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат. Кинематический закон равнопеременного движения Закон равноускоренного движения получается в результате решения простейшего дифференциального уравнения вида: Общее решение этого уравнения дается формулой: ;Здесь и — произвольные константы, соответствующие начальной координате и начальной скорости.

В случае тела, брошенного под произвольным углом к горизонту, из равенств и хорошо известные соотношения для времен полета, подъема и спуска максимальной высоты подъема: , дальности полета: .

И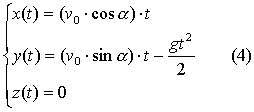 сключая из двух первых равенств системы время, легко получить уравнение траектории:

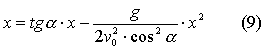
Преобразования Галилея. Механический принцип относительности

В классической механике справедлив механический принцип относительности (принцип относительности Галилея): законы динамики одинаковы во всех инерциальных систе­мах отсчета.

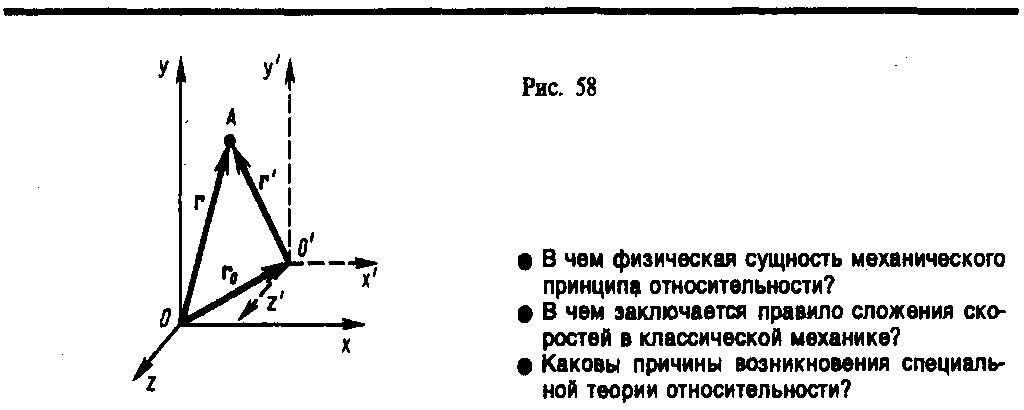
Для его доказательства рассмотрим две системы отсчета: инерциальную систему K (с координатами х, у, z), которую условно будем считать неподвижной, и систему K' (с координатами x', у', z'), движущуюся относительно K равномерно и прямолинейно со скоростью u (u=const). Отсчет времени начнем с момента, когда начала координат обеих систем совпадают. Пусть в произвольный момент времени t расположение этих систем друг относительно друга имеет вид, изображенный на рис. 58. Скорость u направлена вдоль OO', радиус-вектор, проведенный из О в О', r₀=ut.

Найдем связь между координатами произвольной точки А в обеих системах. Из рис. 58 видно, что

(34.1)

Уравнение (34.1) можно записать в проекциях на оси координат:

(34.2)

Уравнения (34.1) и (34.2) носят название преобразований координат Галилея.

В частном случае, когда система К' движется со скоростью т вдоль положительного направления оси х системы К (в начальный момент времени оси координат совпадают), преобразования координат Галилея имеют вид

В классической механике предполагается, что ход времени не зависит от относи­тельного движения систем отсчета, т. е. к преобразованиям (34.2) можно добавить еще одно уравнение:

(34.3)

Записанные соотношения справедливы лишь в случае классической механики (u<<с), а при скоростях, сравнимых со скоростью света, преобразования Галилея заменяются более общими преобразованиями Лоренца* (§ 36).

Продифференцировав выражение (34.1) по времени (с учетом (34.3)), получим уравнение

(34.4)

которое представляет собой правило сложения скоростей в классической механике.

Ускорение в системе отсчета К

Таким образом, ускорение точки А в системах отсчета К и К', движущихся друг относительно друга равномерно и прямолинейно, одинаково:

(34.5)

Следовательно, если на точку А другие тела не действуют (а=0), то, согласно (34.5), и а'=0, т. е. система К' является инерциальной (точка движется относительно нее равномерно и прямолинейно или покоится).

Таким образом, из соотношения (34.5) вытекает подтверждение механического принципа относительности: уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т. е. являются инвариантными по отношению к преобразованиям координат. Галилей обратил внимание, что никакими механичес­кими опытами, проведенными в данной инерциальной системе отсчета, нельзя устано­вить, покоится ли она или движется равномерно и прямолинейно. Например, сидя в каюте корабля, движущегося равномерно и прямолинейно, мы не можем определить, покоится корабль или движется, не выглянув в окно.

Кинема́тика твёрдого тела— раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины.

Различают пять видов движения твердого тела: 1) поступательное; 2)вращение вокруг неподвижной оси; 3) плоское движение; 4) движение вокруг неподвижной точки и 5) свободное движение. Первые два вида являются основными движениями твердого тела. Число степеней свободы твердого тела i – это число независимых координат, однозначно определяющих положение твердого тела в пространстве.