
- •17) Осевое растяжение – сжатие стержней.Построение эпюр n
- •Продольные силы в поперечных сечениях
- •20) Статически неопределимые задачи при растяжении сжатии
- •22) Площадь плоских сечений статистические моменты и моменты инерции
- •Статические моменты сечения
- •23) Моменты инерций относительно параллельных осей.Поворот осей
- •24) 2.4. Главные оси и главные моменты инерции
- •Кручение вызывается:
- •27)Кручение стержней прямоугольного сечения
- •30) Напряжение и расчет на прочность
17) Осевое растяжение – сжатие стержней.Построение эпюр n
Продольные силы в поперечных сечениях
Под
растяжением
(сжатием)
понимают такой вид нагружения, при
котором в поперечных сечениях стержня
возникают только продольные силы
![]() ,
а прочие силовые факторы равны нулю.
,
а прочие силовые факторы равны нулю.
Рассмотрим
однородный прямолинейный стержень
длиной ![]() и площадью поперечного сечения А,
на двух концах которого приложены
две равные по величине и противоположно
направленные центральные продольные
силы Р
(рис. 2.2, а).
и площадью поперечного сечения А,
на двух концах которого приложены
две равные по величине и противоположно
направленные центральные продольные
силы Р
(рис. 2.2, а).
Продольная сила – внутреннее усилие, равное сумме проекций всех внешних сил, взятых с одной стороны от сечения, на ось стержня. Примем следующее правило знаков для продольной силы: растягивающая продольная сила положительна, сжимающая – отрицательна (рис. 2.1).
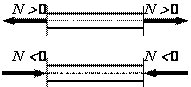
Рис.2.1
Поместим
начало плоской системы координат yz
в центре тяжести левого сечения, а ось
![]() направим
вдоль продольной оси стержня.
направим
вдоль продольной оси стержня.
Для
определения величин внутренних усилий
воспользуемся методом сечений. Задавая
некоторое сечение на расстояние z
(![]() )
от начала системы координат и рассматривая
равновесие левой относительно заданного
сечения части стержня (рис. 2.2, б),
приходим к следующему уравнению:
)
от начала системы координат и рассматривая
равновесие левой относительно заданного
сечения части стержня (рис. 2.2, б),
приходим к следующему уравнению:
![]() ,
,
2.
Определяем продольную силу
![]() в
каждом характерном сечении. При этом
рассматриваем всегда ту отсеченную
часть, в которую не попадает жесткая
заделка.
в
каждом характерном сечении. При этом
рассматриваем всегда ту отсеченную
часть, в которую не попадает жесткая
заделка.
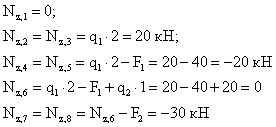
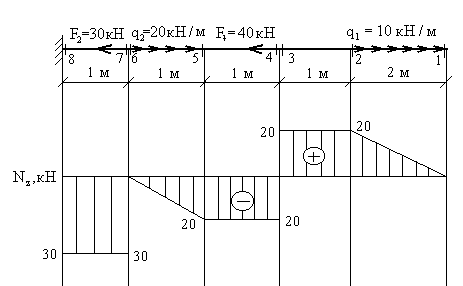
3. По найденным значениям строим эпюру .
Положительные значения откладываются (в выбранном масштабе) над осью эпюры, отрицательные – под осью.
![]() ,
(2.3)
,
(2.3)
где
![]() - площадь
поперечного сечения нетто;
- площадь
поперечного сечения нетто;
![]() -
площадь поперечного сечения брутто;
-
площадь поперечного сечения брутто;
![]() -
площадь его ослабления
-
площадь его ослабления
,
19) ДЕФОРМАЦИИ
И ПЕРЕМЕЩЕНИЯ ПРИ РАСТЯЖЕНИИ - СЖАТИИ
При растяжении и сжатии бруса
меняются его продольные и поперечные
размеры (рис.2.4).
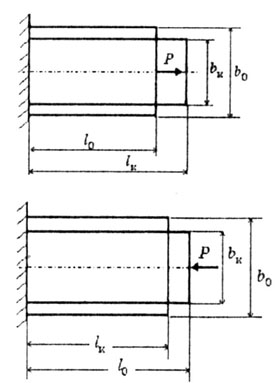 Рис.
2.4 При растяжении: Длина бруса меняется
на
Рис.
2.4 При растяжении: Длина бруса меняется
на
![]() (удлинение),
Ширина бруса меняется на
(удлинение),
Ширина бруса меняется на
![]() (сужение).
При сжатии:
(сужение).
При сжатии:
![]() (укорочение)
(укорочение)
![]() (увеличение
Закон Гука выражает прямо пропорциональную
зависимость между нормальным напряжением
и относительной деформацией:
(увеличение
Закон Гука выражает прямо пропорциональную
зависимость между нормальным напряжением
и относительной деформацией:
![]() или,
если представить в другом виде:
или,
если представить в другом виде:
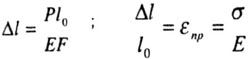 где
Е - модуль продольной упругости. Это
физическая постоянная материапа,
характеризующая его способность
сопротивпяться упругому деформированию.
EF - жесткость поперечного сечения бруса
при эастяжении-сжатии.
где
Е - модуль продольной упругости. Это
физическая постоянная материапа,
характеризующая его способность
сопротивпяться упругому деформированию.
EF - жесткость поперечного сечения бруса
при эастяжении-сжатии.
абсолютная деформация (см, м) |
относительная деформация безразмерная |
|
|
|
|
b поперечная |
|
Деформация
бруса (растяжение ипи сжатие) вызывает
перемещение поперечных сечений.
Рассмотрим три случая нагружения при
растяжении. В первом случае при растяжении
бруса сечение n-n перемещается в положение
n1-n1
на величину
.
Здесь: перемещение сечения равно
деформации (удлинению) бруса
=
l.
(рис.2.5).
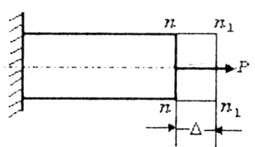 Рис.
2.5 Во втором случае растяжения (рис. 2.6)
Рис.
2.5 Во втором случае растяжения (рис. 2.6)
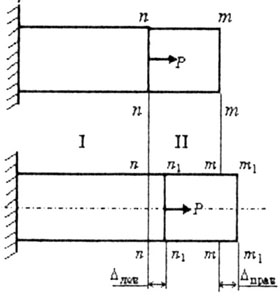 Рис.
2.6 l-ый участок бруса деформируется
(удлиняется) на величину
l1,
сечение n-n перемещается в положение
n1-n1
на величину
лев
=
l1.
ll-ой участок бруса не деформируется,
так как здесь отсутствует продольная
сила N, сечение m-m перемещается в положение
m1-m1
на величину
Рис.
2.6 l-ый участок бруса деформируется
(удлиняется) на величину
l1,
сечение n-n перемещается в положение
n1-n1
на величину
лев
=
l1.
ll-ой участок бруса не деформируется,
так как здесь отсутствует продольная
сила N, сечение m-m перемещается в положение
m1-m1
на величину
![]() В
третьем случае рассмотрим деформации
бруса при схеме нагружения, представленной
на рисунке (рис.2.7).
В
третьем случае рассмотрим деформации
бруса при схеме нагружения, представленной
на рисунке (рис.2.7).
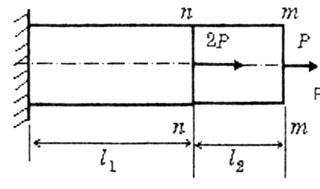 Рис.
2.7 В этом примере: перемещение сечения
n-n (
лев)
равно удлинению 1-ого участка бруса:
Рис.
2.7 В этом примере: перемещение сечения
n-n (
лев)
равно удлинению 1-ого участка бруса:
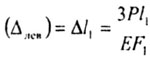 Сечение
m-m переместится в положение m1-m1
за счет деформации 1-ого участка бруса,
а в положение m2-m2
за счет своего собственного удлинения
(рис.2.8):
Сечение
m-m переместится в положение m1-m1
за счет деформации 1-ого участка бруса,
а в положение m2-m2
за счет своего собственного удлинения
(рис.2.8):
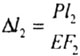 Суммарное
перемещение сечения m-m:
Суммарное
перемещение сечения m-m:
![]() В
данном случае:
В
данном случае:
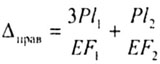
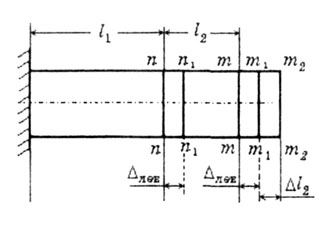 Рис.
2.8 С использованием эпюры N получаем
такой же результат (снимаем N с эпюры)
(рис.2.9).
Рис.
2.8 С использованием эпюры N получаем
такой же результат (снимаем N с эпюры)
(рис.2.9).
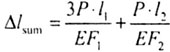
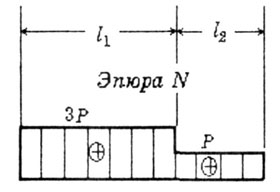 Рис.
2.9 Перемещение конца консоли можно
получить, используя только внешние силы
(2Р,Р). Тогда:
Рис.
2.9 Перемещение конца консоли можно
получить, используя только внешние силы
(2Р,Р). Тогда:
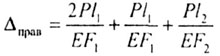

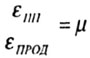 коэффициент
поперечной деформации, коэффициент
Пуассона
коэффициент
поперечной деформации, коэффициент
Пуассона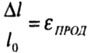 продопьная
продопьная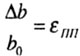 поперечная
поперечная