9. Консервативные (потенциальные) силы. Потенциальная энергия системы матер точек. Связь силы и потенциальной энергии.

Консервативные силы: консервати́вные си́лы (потенциальные силы) — силы, работа которых не зависит от формы траектории (зависит только от начальной и конечной точки приложения сил). Отсюда следует определение: консервативные силы — такие силы, работа которых по любой замкнутой траектории равна 0.

Если в системе действуют только консервативные силы, то механическая энергия системы сохраняется.

Для консервативных сил выполняются следующие тождества:

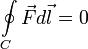• — работа консервативных сил по произвольному замкнутому контуру равна 0;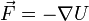

• — консервативная сила является градиентом некой скалярной функции , называемой силовой. Эта функция равна потенциальной энергии взятой с обратным знаком.

силы разделяют на консервативные и неконсервативные. Примерами консервативных сил являются: сила тяжести, сила упругости. Примерами неконсервативных сил являются сила трения и сила сопротивления среды.

Потенциальная энергия системы матер точек:

Потенциальная энергия  — скалярная физическая величина, характеризующая способность некого тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы

Потенциальная энергия принимается равной нулю для некоторой конфигурации тел в пространстве, выбор которой определяется удобством дальнейших вычислений. Процесс выбора данной конфигурации называется нормировкой потенциальной энергии.

Корректное определение потенциальной энергии может быть дано только в поле сил, работа которых зависит только от начального и конечного положения тела, но не от траектории его перемещения. Такие силы называются консервативными.

Также потенциальная энергия является характеристикой взаимодействия нескольких тел или тела и поля.

Любая физическая система стремится к состоянию с наименьшей потенциальной энергией.

Потенциальная энергия упругой деформации характеризует взаимодействие между собой частей тела.

Если задано положение каждой материальной точки, то этим определено и положение всей системы или ее конфигурация. Если силы, действующие на материальные точки системы, зависят только от конфигурации системы (т.е. только от координат материальных точек) и сумма работ этих сил при перемещении системы из одного положения в другое не зависит от пути перехода, а определяется только начальной и конечной конфигурациями системы, то такие силы называются консервативными. В этом случае для системы материальных точек также можно ввести понятие потенциальной энергии системы, обладающей свойством (7): , (8)

где - полная работа консервативных сил, действующих на материальные точки системы при переходе ее из конфигурации 1 в конфигурацию 2; и - значения потенциальной энергии системы в этих конфигурациях.

Связь между силой, действующей на тело в данной точке поля, и его потенциальной энергией определяется по следующим формулам: или ,

где - называется градиентом скалярной функции ; - единичные векторы координатных осей;

Связь силы и потенциальной энергии.

Каждой точке потенциального поля соответствует, с одной стороны, некоторое значение вектора силы , действующей на тело, и, с другой стороны, некоторое значение потенциальной энергии . Следовательно, между силой и потенциальной энергией должна существовать определенная связь. Для установления этой связи вычислим элементарную работу , совершаемую силами поля при малом перемещении тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой . Эта работа равна где - проекция силы на направление .Поскольку в данном случае работа совершается за счет запаса потенциальной энергии , она равна убыли потенциальной энергии на отрезке оси : Из двух последних выражений получаем

Откуда Последнее выражение дает среднее значение на отрезке . Чтобы

получить значение в точке нужно произвести предельный переход:

Так как может изменяться не только при перемещении вдоль оси , но также и при перемещениях вдоль других направлений, предел в этой формул представляет робой так называемую частную производную от по :

Это соотношение справедливо для любого направления в пространстве, в частности и для направлений декартовых координатных осей х, у, z:

Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы: в математике вектор ,

где а - скалярная функция х, у, z, называется градиентом этого скаляра обозначается символом . Следовательно сила равна градиенту потенциальной энергии, взятого с обратным знаком