Двумерный алгоритм Лианга-Барски

В 1982 г. Лианг и Барски предложили алгоритмы отсечения прямоугольным окном с использованием параметрического представления для двух, трех и четырехмерного отсечения.

Продолжим каждую из четырех границ окна до бесконечных прямых. Каждая из таких прямых делит плоскость на 2 области. Назовем "видимой частью" ту, в которой находится окно отсечения.Пусть конечные точки отрезка есть V₀ и V₁ с координатами (x0,y0) и (x1,y1), соответственно. Тогда параметрическое представление линии может быть задано следующим образом:

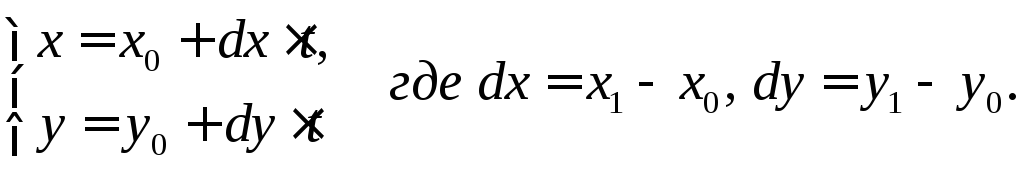
Или в общем виде для отрезка, заданного точками V₀ и V₁: V(t)    =   V₀   +  (V₁   -  V₀)   ·  t

Для точек V₀ и V₁ параметр t равен 0 и 1, соответственно. Меняя t от 0 до 1 перемещаемся по отрезку V₀V₁ от точки V₀ к точке V₁. Изменяя t в интервале от -∞ до +∞, получаем бесконечную (далее удлиненную) прямую, ориентация которой - от точки V₀ к точке V₁.

Подставляя параметрическое представление, заданное уравнениями, в неравенства, получим следующие соотношения для частей удлиненной линии, которая находится в окне отсечения:

-dx·t ≤ x0   -  Xлев и dx·t ≤ Xправ   -  x0,

-dy·t ≤ y0   -  Yниз и dy·t ≤ Yверх   -  y0.

Заметим, что в этих соотношениях - неравенства, описывающие внутреннюю часть окна отсечения, в то время как равенства определяют его границы. Рассматривая неравенства, они имеют одинаковую форму вида: P_i·t    ≤   Q_i       для   i   = 1,2,3,4.

Тогда каждое неравенство задает диапазон значений параметра t, для которых эта удлиненная линия находится на видимой стороне соответствующей линии границы. Более того, конкретное значение параметра t для точки пересечения есть t = Q_i/P_i. Причем знак Q_i показывает на какой стороне соответствующей линии границы находится точка V₀. А именно, если Qi ≥ 0, тогда V₀ находится на видимой стороне линии границы, включая и ее. Если же Q_i    <   0, тогда V₀ находится на невидимой стороне. Ясно, что любое P_i может быть меньше 0, больше 0 и равно 0.

Билет 14

Вопрос 45

Стандартизация в машинной графике: стандарты, структура прикладной графической системы, переносимость, этапы преобразования координатной информации, метафайлы.

Постепенно сформировалось представление о программном продукте как о промышленном изделии, что выдвинуло проблему стандартизации графического программного обеспечения. Развитие сетей ЭВМ, оснащенных терминальными устройствами различных типов, потребовало обеспечить независимость программного обеспечения от аппаратуры.

Было установлено, что основная цель стандартизации - переносимость графических систем, которая достигается стандартизацией интерфейса между графическим ядром системы (базовой графической системой), реализующим собственно графические функции, и моделирующей системой - проблемно-ориентированной прикладной программой, использующей функции графического ядра. Базовая система должна обладать: независимостью от вычислительных систем; независимостью от языков программирования; независимостью от области применения; независимостью от графических устройств.

Структура прикладной графической системы, удовлетворяющей сформулированным требованиям, может быть представлена в виде шестиуровневой модели.

П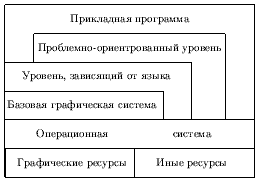роцесс преобразования информации при выполнении вывода:

1. Модельные преобразования. формируется описание совокупного объекта в некоторой единой (мировой) системе координат. Описание совокупного объекта подается в графическую систему.

2. Нормализующие преобразования. переводит описание из мировой, системы координат в т.н. нормализованные координаты устройства.

3. Преобразования сегментов.

4. Видовые преобразования. В случае 3D описания изображения и 2D устройства вывода необходимо выполнить проецирование изображения на заданную картинную плоскость. Наоборот, при 2D сцене и 3D устройстве вывода необходимо выполнить преобразование, связанное с размещением изображения

5. Преобразование рабочей станции- преобразование данных из аппаратно-независимой формы в координаты устройства.

Процесс преобразования координатной информации при вводе от координатных устройств обратен.

Аппаратно-независимый графический протокол или метафайл представляют собой процедурное описание изображения в функциях виртуального графического устройства. Он обеспечивает возможность запоминать графическую информацию единым образом, передавать ее между различными графическими системами (в том числе работающими на различных ЭВМ) и интерпретировать информацию для вывода на различные графические устройства. Для интерпретации метафайла требуется локальная ЭВМ, выполняющая эмуляцию не реализованных в аппаратуре функций и кодирование в команды конкретных устройств.

Основными стандартами являются:

1. GKS (Graphical Kernel System) - набор базовых функций для 2D аппаратно-независимой машинной графики.

2. GKS-3D (Graphical Kernel System for 3 Dimensions) - расширение GKS для поддержки базовых функций в 3D.

3. PHIGS (Programmer's Hierarchical Interactive Graphics System) - набор базовых функций 3D ориентированной на непосредственный вывод графических примитивов

4. Языковые интерфейсы

5. CGM аппаратно-независимый формат обмена графической информацией.

6. CGI (Computer Graphics Interafce) - набор базовых элементов для управления и обмена данными между аппаратно-независимым и аппаратно-зависимым уровнями графической системы.

7. CGRM (Computer Graphics Reference Model) - модель стандартов в машинной графике, которая определяет концепции и взаимосоотношения применительно к будущим стандартам в машинной графике.

8. Регистрация.

9. Тестирование реализаций на соответствие графическим стандартам