19. Растровое представление отрезка: постановка задачи, алгоритм Брезенхейма.

Процесс определения пикселов, наилучшим образом аппроксимирующих заданный отрезок, называется разложением отрезка в растр.

И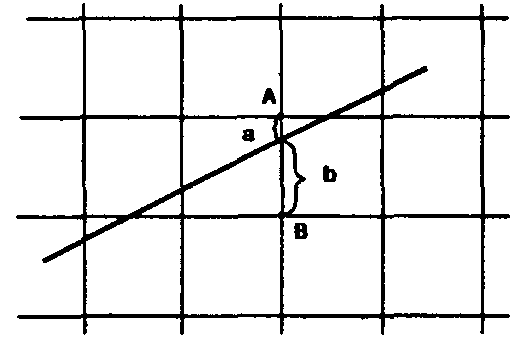дея алгоритма состоит в том, что в процессе построения отрезка одна из координат - либо “х”, либо “y” (в зависимости от углового коэффициента) - изменяется на единицу. Изменение другой координаты (либо на нуль, либо на единицу) зависит от расстояния между “теоретическим” положением отрезка и ближайшими координатами сетки (такое расстояние в алгоритме называется “ошибкой”).

При построении растрового изображения отрезка всегда выбирается ближайший по вертикали пиксел. При этом из двух точек А и В выбирается та, которая ближе к исходной прямой (в данном случае выбирается точка А, так

как а < b).

При совмещении начала координат с одним из концов отрезка, имеем три возможные оси симметрии, и достаточно рассмотреть половину одного квадранта, например ту, для которой dx >= dy >= 0.

Уравнение прямой, описывающее отрезок:

представляет собой функцию ошибок, которая должна быть минимизирована по абсолютной величине в процессе генерирования. Оно становится равным нулю, когда точка находится на прямой.

Пусть E = y*dx - x*dy. (1)

Если за исходную точку принять начало координат, то достаточно двух элементарных движений, чтобы с их помощью перемещаться вдоль отрезка.

Движение A: увеличение x

x = x + 1; в результате согласно (1) ошибка уменьшается на величину dy:

E = E - dy;

Движение B: увеличение x и y

x = x + 1;

y = y + 1;

приводит в соответствии с (1) к возрастанию E на величину (dx - dy), имеющую положительное значение в рассматриваемой половине квадранта:

E = E + dx - dy;

исходя из этих соображений, построен итерационный алгоритм минимизации ошибки, при котором на каждом шаге выбирается соответствующее движение:

Этот алгоритм имеет два недостатка:

1. первое движение выбирается произвольно

2. ошибка изменяется от dx-dy до -dy и случайным образом большинство точек может расположиться выше или ниже истинного отрезка.

Обе проблемы отпадают, если центрировать функцию ошибки относительно нуля, начиная с величины (dy -dx/2):

E = dy - dx/2.

Билет 10

9. Алгоритмы архивации с потерями, проблемы алгоритмов архивации с потерями. Основные идеи алгоритмов jpeg, фрактальный, волновой.

Несжимаемость многих изображений привела к созданию нового типа алгоритмов – сжимающих с потерей информации. Коэффициент архивации и степень потерь качества в них можно задавать. При этом достигается компромисс между размером и качеством изображений.

Одна из серьезных проблем машинной графики заключается в том, что до сих пор не найден адекватный критерий оценки потерь качества изображения. Потери происходят постоянно – при оцифровке, при переводе в ограниченную палитру цветов, при переводе в другую систему цветопредставления для печати и, что особенно важно, при архивации с потерями.

Отличной считается архивация, при которой невозможно на глаз различить первоначальное и разархивированное изображения. Хорошей – когда можно сказать, какое из изображений подвергалось архивации, можно только сравнивая две находящиеся рядом картинки. При дальнейшем увеличении степени сжатия, как правило, становятся заметны побочные эффекты, характерные для данного алгоритма.

JPEG – один из самых новых и достаточно мощных алгоритмов. Разработан группой экспертов в области фотографии специально для сжатия 24-битных изображений. Оперирует алгоритм областями 8х8, на которых яркость и цвет меняются сравнительно плавно. Вследствие этого при разложении матрицы такой области в двойной ряд по косинусам значимыми оказываются только первые коэффициенты. коэффициенты. Таким образом, сжатие в JPEG осуществляется за счет плавности изменения цветов в изображении. Метод позволяет сжимать некоторые изображения в 10-15 раз без серьезных потерь.

Фрактальная архивация основана на том, что изображение представляется в более компактной форме – с помощью коэффициентов системы итерируемых функций (IFS). IFS представляет собой набор трехмерных аффинных преобразований, переводящих одно изображение в другое. Преобразованию подвергаются точки в трехмерном пространстве (х-координата, у-координата, яркость). Фрактальная компрессия – это поиск самоподобных областей в изображении и определение для них параметров аффинных преобразований. Подавляющее большинство исследований в области фрактальной компрессии сейчас направлены на уменьшение времени архивации, необходимого для получения качественного изображения.

Рекурсивный (волновой) алгоритм исходит из идеи использования когерентности областей. Ориентирован алгоритм на цветные и черно-белые изображения с плавными переходами. Идея алгоритма заключается в том, что в файле сохраняется разница – число между средними значениями соседних блоков в изображении, которая обычно принимает значения, близкие к 0. К достоинствам этого алгоритма можно отнести то, что он очень легко позволяет реализовать возможность постепенного “проявления” изображения при передаче его по сети.