
- •13. Аффинные преобразования на плоскости.
- •Билет 2
- •2. История развития кг. Современные тенденции развития кг.
- •12. Аффинные преобразования, их свойства, однородные координаты.
- •Билет 3
- •3. Основные понятия кг. Аппаратное обеспечение кг. Принципы формирования изобр.
- •15. Проецирование. Общий вид преобразований в пространстве. Виды проекций.
- •Общая формула преобразования
- •4. Архитектура рабочих станций. Графический ускоритель. Арi.
- •14. Аффинные преобразования в пространстве. Использование матричного представления. Составные аффинные преобразования в пространстве.
- •5. Архитектура графических рабочих станций. Технологии 3d графики.
- •16. Этапы создания графического объекта. Преобразование положения объекта. Понятие камеры. Особенности матричных преобразований.
- •7. Общие положения алгоритмов сжатия изображений.
- •17. Понятие растрового алгоритма. Понятие связности. Основные требования предъявляемые к растровым алгоритмам.
- •18. Растровое представление отрезка: постановка задачи, простейший алгоритм, алгоритм цда.
- •20. Растровое представление отрезка: построение сглаженной линии (метод Флойда-Стейнберга, модификация алгоритма Брезенхейма, сглаживание всей сцены).
- •8. Алгоритмы архивации без потерь: rle, lz/lzw, Хаффман.
- •19. Растровое представление отрезка: постановка задачи, алгоритм Брезенхейма.
- •9. Алгоритмы архивации с потерями, проблемы алгоритмов архивации с потерями. Основные идеи алгоритмов jpeg, фрактальный, волновой.
- •21. Растровое представление окружности: постановка задачи, простой алгоритм, алгоритм Брезенхейма.
- •10. Геометрическое моделирование и решаемые им задачи…
- •22. Алгоритм закраски области, заданной цветом границы.
- •Билет 12
- •11. Представление геометрических моделей. Полигональные сетки и способы …
- •Задача отсечения Вопрос 23
- •Двумерный алгоритм Коэна-Сазерленда (Кохена-Сазерленда)
- •Двумерный fc-алгоритм
- •Вопрос 44
- •Интерактивные системы машинной графики
- •Графические языки высокого уровня
- •Синтаксические расширения алгоритмических языков
- •Процедурные графические языки
- •Задача отсечения Вопрос 24
- •Двумерный алгоритм Лианга-Барски
- •Вопрос 45
- •Задача отсечения Вопрос 25
- •Двумерный алгоритм Кируса-Бека
- •10. Геометрическое моделирование и решаемые им задачи…
- •Пирамидальное фильтрование (Mip-mapping).
- •Проверка выпуклости и определение нормалей Вопрос 27 Алгоритм с использованием векторных произведений
- •Разбиение невыпуклых многоугольников. Алгоритм метода при обходе вершин многоугольника против часовой стрелки состоит в следующем:
- •Отсечение многоугольника
- •Трассировка лучей
- •Излучательность
- •3. Основные понятия кг. Аппаратное обеспечение кг. Принципы формирования изобр.
- •4. Архитектура рабочих станций. Графический ускоритель. Арi.
- •Вопрос 30
- •5. Архитектура графических рабочих станций. Технологии 3d графики.
- •6. Архитектура графических рабочих станций. Принципы конвейерной архитектуры.
- •Пересечение луча с плоскостью и многоугольником Вопрос 32
- •7. Общие положения алгоритмов сжатия изображений.
- •8. Алгоритмы архивации без потерь: rle, lz/lzw, Хаффман.
- •9. Алгоритмы архивации с потерями, проблемы алгоритмов архивации с потерями. Основные идеи алгоритмов jpeg, фрактальный, волновой.
- •10. Геометрическое моделирование и решаемые им задачи…
- •Вопрос 37
- •11. Представление геометрических моделей. Полигональные сетки и способы …
- •Вопрос 38
- •Вопрос 44
- •Интерактивные системы машинной графики
- •Графические языки высокого уровня
- •Синтаксические расширения алгоритмических языков
- •Процедурные графические языки
- •Вопрос 39
- •10. Геометрическое моделирование и решаемые им задачи…
- •Вопрос 41
21. Растровое представление окружности: постановка задачи, простой алгоритм, алгоритм Брезенхейма.
Из геометрии мы знаем, что окружность с центром в точке (xc,yc) и радиусом r, задается параметрически с помощью системы уравнений:
![]()
Отсюда не сложно получить алгоритм генерации окружности:
Полагаем А=0.
Если А больше либо равно 2, то окружность отрисована.
Вычислим x=Trunc(xc+r*cos(A)), y=Trunc(yc+r*sin(A))
Screen[x,y]=Color
Увеличим A на d и перейдем к шагу 2.
В данном алгоритме d подбираем в зависимости от радиуса окружности и разрешающей способности устройства вывода. Основная причина, по которой использование данного алгоритма нецелесообразно – очень низкая скорость работы, связанная с использованием вещественных чисел, и тем более вычислением тригонометрических функций.
 Если точка (x,y)
лежит на окружности с центром в точке
(0,0),
то и точка (x,-y),
так же лежит на этой окружности. Последнее
утверждение можно развить, а именно:
если точка (x,y)
лежит на окружности с центром в точке
(0,0),
то и точки
(x,-y);(-x,-y);(-x,y);(y,x),(y,-x);(-y,-x);(-y,x),
так же лежат на этой окружности.
Координата x
увеличивается на единицу на каждом
шаге. Так же координата y
либо уменьшается на единицу, либо
остается без изменений. Нужно выбрать,
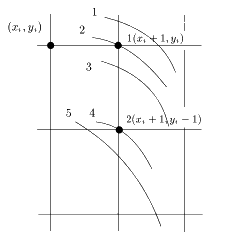
куда переходить из точки (xi,yi)
либо в точку (xi+1,yi),
либо в точку (xi+1,yi-1).
Для того, чтобы осуществить выбор
рассмотрим две невязки:
Если точка (x,y)
лежит на окружности с центром в точке
(0,0),
то и точка (x,-y),
так же лежит на этой окружности. Последнее
утверждение можно развить, а именно:
если точка (x,y)
лежит на окружности с центром в точке
(0,0),
то и точки
(x,-y);(-x,-y);(-x,y);(y,x),(y,-x);(-y,-x);(-y,x),
так же лежат на этой окружности.
Координата x
увеличивается на единицу на каждом
шаге. Так же координата y
либо уменьшается на единицу, либо
остается без изменений. Нужно выбрать,
куда переходить из точки (xi,yi)
либо в точку (xi+1,yi),
либо в точку (xi+1,yi-1).
Для того, чтобы осуществить выбор
рассмотрим две невязки:
di1=(xi+1)2+yi2-r2
di2=(xi+1)2+(yi-1)2-r2
А так же будем следить за их суммой:
di=di1+di2
Рассмотрим несколько вариантов расположения "вещественной" окружности относительно "целых" точек:
Случай 1. di1 < 0, di2 < 0, и следовательно di < 0. Случай 2. di1= 0, di2 < 0, и следовательно di < 0. Случай 3. di1 > 0, di2 < 0, и следовательно имеем два варианта для di: Случай 3.1. |di1| < |di2| и следовательно di < 0. Случай 3.2. |di1| > |di2| и следовательно di > 0. Случай 4. di1 > 0, di2=0, и следовательно di > 0: Случай 5. di1 > 0, di2 > 0, и следовательно di > 0:
В случае, если di < 0 надо активировать точку (xi+1,yi), а в случае, если di > 0 надо активировать точку (xi+1,yi-1). di=di1+di2=(xi+1)2+yi2-r2+(xi+1)2+(yi-1)2-r2=2xi2+2yi2+4xi-2yi+3-2r2
Теперь получим выражение di+1 через di .
di+1=2xi+12+2yi+12+4xi+1-2yi+1+3-2r2=di+4(xi-yi)+10
Осталось получить значение d1 в начальной точке (x1=0,y1=r):
d1=3-2r
Если x > y, то выходим.
1. Screen[x+xc,y+yc]:=Color;
2. Screen[x+xc,-y+yc]:=Color;
3. Screen[-x+xc,y+yc]:=Color;
4. Screen[-x+xc,-y+yc]:=Color;
5. Screen[y+xc,x+yc]:=Color;
6. Screen[y+xc,-x+yc]:=Color;
7. Screen[-y+xc,x+yc]:=Color;
8. Screen[-y+xc,-x+yc]:=Color;
Если d < 0, то d:=d+4*x+6, переходим на Шаг 13
d:=d+4(x-y)+10; y:=y-1;
Билет 11
10. Геометрическое моделирование и решаемые им задачи…
Модель – это представление некоторых, необязательно всех, свойств объекта, либо конкретно существующего, либо абстрактного, его особенностей.
При оценке степени соответствия синтезированных изображений и оригинала в телевидении и кинематографе используются три уровня подобия:
1. Физическое подобие означает, что изображение по основным физическим характеристикам повторяет оригинал. Подобие считается физически полным, если характеристики оригинала и изображения полностью подобны или строго пропорциональны.
2. Психофизическое (физиологическое) – соответствие на уровне зрительных ощущений, например фотореалистичная графика.
3. Психологическое – предполагает лишь некоторую схожесть между объектом и изображением: чертежи, проволочные модели и т.п
геометрические модели – это модели состоящие из след компонентов:
- пространственное расположение и форма – геометрия объекта; некоторые атрибуты: цвет, текстура;
- топология (связность с другим объектом).
Способы представления объектов:
Аналитическая модель – это набор чисел и, если необходимо, логических параметров, которые играют роль коэффициентов и других величин в уравнениях, аналитических соотношениях, задающих объект данного типа.
Координатные модели – это наборы точек, принадлежащих объектам, которые задаются координатами.
У координатных моделей могут быть разновидности:
- координатно-разностные модели, где вместо координат их разности;
- помимо координат, в каждой точке могут быть указаны дополнительные характеристики(проекции нормалей, векторов, значения каких-либо параметров и т.п.);
- могут быть дополнены кодами, управляющими командами (при описании нескольких кривых это могут быть команды окончания кривых, коды завершения моделей и т.п.);
- приближенные координатные модели; предполагается, что в связи с погрешностями измерений и другими факторами точки этих моделей смещены относительно их правильного положения, тогда здесь возникает задача аппроксимации – поиска такой линии или поверхности, которые бы проходили как можно ближе к заданным точкам.
Декартова система координат – основа численного моделирования объектов.
Одну и ту же фигуру можно задать разными способами, но обычно выделяют те, для которых количество параметров минимально. Это минимальное количество называют параметрическим числом образа.
В задании объекта могут также участвовать логические параметры. Эти параметры не влияют на параметрические числа объектов и можно ограничиться числами 0 и 1 или же установить параметр по знаку числа. Так же очень важно задавать направление вычерчивания, которое необходимо для определения видимости сторон. Для этого используют касательные векторы, или векторы направления.
