35. Модели распределенных лагов

Во многих экономических задачах встречаются лагированные (взятые в предыдущий момент времени) переменные. Например, Y_t – выпуск предприятия в год t, может зависеть не только от инвестиций I_t этот год, но и от инвестиций в предыдущие годы:

.

Такие модели встречаются всякий раз, когда эндогенная переменная с запаздыванием реагирует на изменения экзогенной переменной. При этом в модели могут использоваться лагированные значения экзогенной или эндогенной переменной или одновременно и те, и другие. Для статистического моделирования полезно различать два случая.

Обе модели:

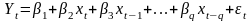(12.7)

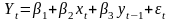(12.8)

включают в себя лагированные значения переменных, но существенно различаются с точки зрения статистического оценивания параметров. Действительно, в (12.7) регрессоры некоррелированы с ошибками (мы здесь предполагаем, что независимая переменная x_t детерминированная). Поэтому (12.7) можно оценивать с помощью МНК. В модели (12.8) y_t-1 включает в себя _t-1 поэтому вектор ошибок  и матрица регрессоров X коррелированы. В этом случае оценки МНК не являются несмещенными.

Уравнение (12.7) является примером модели распределенных лагов, DL. Уравнение (12.8) является авторегрессионной моделью распределенных лагов или динамической моделью, ADL.

Построение моделей с распределенным лагом и моделей авторегрессии имеет свою специфику:

1. Оценка параметров моделей авторегрессии, а в большинстве случаев и моделей с распределенным лагом, не может быть произведена с помощью обычного МНК ввиду нарушения его предпосылок и требует специальных статистических методов.

2. Исследователям приходится решать проблемы выбора оптимальной величины лага и определения его структуры.

3. Между моделями с распределенным лагом и моделями авторегрессии существует определенная взаимосвязь, и в некоторых случаях необходимо осуществлять переход от одного типа моделей к другому.

36. Стационарность процессов

При изучении случайных процессов особо важное место занима­ют процессы, свойства которых остаются инвариантными при любых перемещениях вдоль оси времени.

Ряд у_t называется строго стационарным или стационарным в узком смысле, если совместное распределение т на­блюдений у_t1,y_t2… - ,Уtт не зависит от сдвига по времени, т. е. совпадает с распределением y_t1+1,y_t2+1,… ,y_tm+1 для любых т,t,t_{1, ….,}t_m

Обычно нас интересуют средние значения и ковариации, а не все распределение. Поэтому часто используется понятие слабой стацио­нарности, или стационарности в широком смысле, которое состоит в том, что среднее, дисперсия и ковариации у, не зави­сят от момента времени t.

E(y_t)=μ;

V(y_t)=ν₀;

Соv{у_t, y_t-k) = ν_k.

Конечно, из строгой стационарности следует слабая стационар­ность (при условии конечности первого и второго моментов распреде­ления). В дальнейшем мы будем везде под «стационарностью» пони­мать слабую стационарность.

Введем понятие автокорреляционной функции ACF:

ρ_k= Соv{у_t, y_t-k)/ V(y_t)= ν_k/ ν₀;

Заметим, что р₀ = 1, а !P!< 1. ACF играет важную роль в задаче идентификации моделей временных рядов.

Рассмотрим примеры временных рядов. Самым простым являет­ся ряд с независимыми одинаково распределенными наблюдениями:

Y_t= έ_t, έ_{t ~} iid(0, σ² ), t=1…,n

Этот процесс называется «белым шумом» у него μ = 0, ν₀=о², ν_k = 0, k>0.

Другим примером является АR(1) процесс:

у_t= т+ψуt-1+ έt ,..έ_t,~ iid(0, σ² ), t=1…,n

Предполагается, что |ψ| < 1. В этом случае процесс является ста­ционарным, если его автокорреляционная функция равна ρ_k= ν_k/ ν₀₌ψ^k , k=1,2,...

Важным примером является процесс y_t= y_t-1+έ_t, έ_t,~ iid(0, σ² ) ), t=1…,n,

называемый «случайным блужданием»

Этот процесс является нестационарным.

Отличие процесса АR(1) от «случайного блуждания» в том, что во втором случае влияние возмущений не затухает и равно έ_t+ έ_t-1+ έ_t-2+…

В то время как в процессе АR(1) έ_t+ ψέ_t-1+ψ² έ_t-2+ …

Ещё раз подчеркнем, что условие |ψ| < 1 является обязательным, а обратное условие |ψ| > 1 не встречается в реальных экономических примерах.

Проверка на стационарность

Первое, что следует сделать, - посмотреть на график полученных наблюдений. Возможно, он содержит очевидный на глаз тренд или пе­риодичную компоненту (сезонность). Также возможно, что разброс на­блюдений возрастает или убывает со временем. Это может служить указанием на зависимость среднего значения и соответственно диспер­сии от времени. В обоих случаях ряд будет, скорее всего, нестационарный.

Второе - построить график выборочной автокорреляционной функции (ACF), или коррелограммы:

r_k =ρ_k =

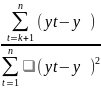
Коррелограмма стационарного временного ряда «быстро убыва­ет» с ростом к после нескольких первых значений. Если же график убывает достаточно медленно, то есть основания предположить неста­ционарность ряда. Кроме АСF, можно также построить график частной автокорреляционной функции РАСF, которая также должна быстро убывать для стационарного процесса.

Третье можно использовать формальные тесты на наличие единичного корня (тест Дики-Фуллера DF, расширенный тест Дики-Фуллера АDF и др.)

В том случай если ряд оказывается не стационарным переходим к уравнению в первых разностях , т.е вводим замену переменных dY_t = Y_t - Y_t-1 и повторяем процедуру проверки на стационарность с 1 пункта.