30. Метод замены переменной (метод подстановки) в неопределенном интеграле.
Методом
подстановки называется метод, при
котором введение новой переменной
позволяет свести исходный
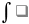к табличному.
Этот метод основан на ТЕОРЕМЕ:
Пусть
функция
определена и дифференцируема на
некотором промежутке Т и пусть множество
Х – множество значений функции, на
котором определена функция
.
Тогда, если на множестве Х функция
имеет первообразную, то на множестве
Т справедлива формула :
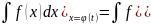
ДОКАЗАТЕЛЬСТВО.
Пусть
-
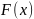первообразная
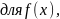пусть
,
рассмотрим функцию
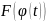и найдем её производную по правилу
дифференцирования сложной функции.
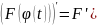
Таким
образом функция
является первообразной для
,
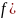значит
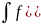
Рассмотрим
функцию
Подставим полученное выражение в равенство (*)
31. Метод интегрирования по частям в неопределенном интеграле.
ТЕОРЕМА.
Пусть функци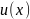и
и
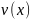определены и дифференцируемы на
некотором промежутке Х и пусть функция
имеет первообразную на этом промежутке.
Тогда на промежутке Х функция
тоже имеет первообразную и справедлива
формула:
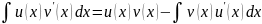или
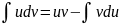
ДОКАЗАТЕЛЬСТВО.
Рассмотрим
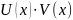и найдем (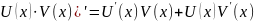
Выразим
второе слагаемое:
Проинтегрируем
это равенство:
Полученная
формула дает возможность свести
вычисление интеграла от
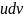к вычислению интеграла от
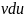, который может оказаться существенно
более простым чем исходный.
Интегрирование
по частям состоит в том, что подынтегральное
выражение заданного интеграла
представляется каким-либо образом в
виде произведения двух сомножителей
.
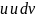После нахождения
используется формула интегрирования
по частям. Эту формулу можно использовать
несколько раз при вычислении одного
интеграла.
Некоторые интегралы, которые интегрируются по частям:
1)
;
;
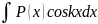(u dv)
2)
;
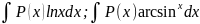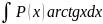( D u V)
3)
;
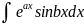( u dv)
32. Определенный интеграл (определение, геометрический смысл).
Пусть функция y=f(x) определена на отрезке [a;b].
1) Разобьем этот отрезок на n произвольных частей точками х0, х1…хn, где х0=a…xn=b.
2)
В каждом отрезке выберем произвольную
точку
и посчитаем значение функции в этой
точке.
3)
Обозначим через
=
4)
Найдем произведение
для всех
.
5)
Составим сумму всех этих произведений
.
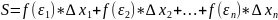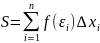
Полученная сумма называется интегральной суммой Римана для функции y=f(x) на [a;b].
Обозначим через λ- максимальный из отрезков,
если n→∞, то λ→0.
ОПРЕДЕЛЕНИЕ. Если существует конечный предел интегральной суммы при n→∞ или, что тоже самое, λ→0, то этот предел называется ОПРЕДЕЛЕННЫМ ИНТЕГРАЛОМ функции f(x) по отрезку [a;b] и обознается
I=
В этом случае числа a и b называются нижним и верхним пределами интегрирования.
f(x) называется подынтегральной функцией.
f(x)dx - подынтегральным выражением
х - переменной интегрирования
[a;b] область интегрирования.
Функция, для которой на отрезке существует определенный интеграл, называется интегрируемой на этом отрезке.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ.
(Криволинейной трапецией называется фигура, ограниченная сверху y=f(x), снизу осью OX. Слева и справа отрезками прямых: x=a b x=b. (рисунок))
Определенный
интеграл от неотрицательной функции
численно равен площади криволинейной
трапеции.
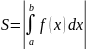
ЗАМЕЧАНИЕ:
Если фигура ограничена 2мя графиками
функций
сверху и
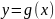снизу, то площадь вычисляется по формуле:
