
- •1. Определение монотонной функции. Необходимое и достаточное условие возрастания функции. Достаточное условие строгого возрастания функции.
- •2. Определение монотонной функции. Необходимое и достаточное условие убывания функции. Достаточное условие строгого убывания функции.
- •3. Определение локального экстремума функции одной переменной. Необходимое условие локального экстремума функции одной переменной.
- •4. Определение локального экстремума функции одной переменной. Первое достаточное условие строгого локального экстремума функции одной переменной.
- •5. Определение локального экстремума функции одной переменной. Второе достаточное условие строгого локального экстремума функции одной переменной.
- •6. Определение выпуклости и вогнутости функции одной переменной (выпуклость вверх, выпуклость вниз). Достаточное условие выпуклости функции одной переменной.
- •7. Определение точки перегиба графика функции одной переменной. Необходимое условие перегиба.
- •8. Определение точки перегиба графика функции одной переменной. Достаточное условие перегиба.
- •9. Определение вертикальной и наклонной асимптоты. Нахождение наклонной асимптоты.
- •10. Наибольшее и наименьшее значение функции одной переменной на замкнутом промежутке.
- •11. Формула Тейлора и формула Маклорена.
- •12. Разложение по формуле Маклорена функции , , .
- •13. Функции нескольких переменных (фнп). Основные определения. Предел фнп.
- •14. Непрерывность фнп. Основные свойства непрерывных функций.
- •15. Частные производные (определение, способы вычисления).
- •16. Частные производные старших порядков. Теорема о независимости смешанных производных от порядка дифференцирования.
- •17. Определение дифференцируемости фнп. Необходимое условие дифференцируемости. Теорема о связи дифференцируемости фнп и существования частных производных.
- •18. Полный дифференциал функции двух переменных.
- •19. Производные сложной функции.
- •20. Определение производной по направлению.
- •21. Определение градиента функции, линии уровня, свойства градиента.
- •22. Определение локального экстремума фнп. Необходимое условие экстремума фнп.
- •23. Определение локального экстремума фнп. Достаточное условие экстремума фнп.
- •24. Условный экстремум функции двух переменных (определение, метод подстановки и метод неопределенных множителей Лагранжа)
- •25. Наибольшее и наименьшее значение фнп в замкнутой и ограниченной области.
- •26. Определение первообразной функции. Теорема о свойствах первообразных функций.
- •27. Определение неопределенного интеграла. Теорема о существовании неопределенного интеграла (достаточное условие).
- •28. Таблица интегралов.
- •29. Свойства неопределенного интеграла.
- •30. Метод замены переменной (метод подстановки) в неопределенном интеграле.
- •31. Метод интегрирования по частям в неопределенном интеграле.
- •32. Определенный интеграл (определение, геометрический смысл).
- •33. Свойства определенного интеграла.
- •34. Интеграл с переменным верхним пределом. Теорема Барроу.
- •35. Формула Ньютона-Лейбница.
- •36. Метод замены переменной (метод подстановки) в определенном интеграле.
- •37. Метод интегрирования по частям в определенном интеграле.
- •38. Определение несобственного интеграла первого рода (по бесконечному промежутку).
- •39. Определение несобственного интеграла второго рода (от функций, имеющих разрыв).
- •40. Понятие о дифференциальных уравнениях. Общее и частное решение. Начальные условия. Задачи Коши.
- •41. Дифференциальные уравнения с разделяющимися переменными и метод их решения.
- •42. Однородные дифференциальные уравнения.
- •43. Линейные уравнения I-порядка.
24. Условный экстремум функции двух переменных (определение, метод подстановки и метод неопределенных множителей Лагранжа)
Условным
extr
функции
называется extr
этой функции при условии, что переменные
x
и y
связаны уравнением
 - уравнение связи.
- уравнение связи.
Таким
образом extr
ищется только на множестве тех точек
плоскости, которые удовлетворяют этому
уравнению. Если в уравнении связи одна
переменная может быть однозначно
выражена через другую, то достаточно
записать
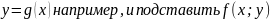 .
Далее обычным способом находится extr
функции одной переменной.
.
Далее обычным способом находится extr
функции одной переменной.
Если
же ниодна переменная не может быть
выражена однозначно через другую, то
в общем случае задачу об искании
условного extr
можно свести к исследованию на обычный
extr
вспомогательной функцией(так называемой
функцией Лагранжа)

Необходимое условие условного экстремума:
Для
того, чтобы точка
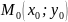 была
точкой условного экстремума функции
была
точкой условного экстремума функции
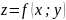 необходимо, чтобы: 1)
необходимо, чтобы: 1)
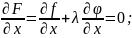
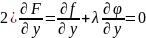 ;
;
3)
В
этой системе 3х уравнений можно найти
переменные
 ,
т.е. стационарную точку
,
т.е. стационарную точку
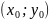 при фиксированном
при фиксированном
 .
.
ДОСТАТОЧНОЕ
УСЛОВИЕ условного экстремума: Пусть в
точке
возможного условного экстремума и её
некоторой окрестности функция
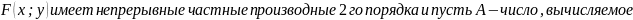 :
:

Причем все частные производные вычислены в стационарной точке, тогда:
1)
если А>0 , то точка точка min
2) если А<0 , то точка
точка max.
точка min
2) если А<0 , то точка
точка max.
25. Наибольшее и наименьшее значение фнп в замкнутой и ограниченной области.
26. Определение первообразной функции. Теорема о свойствах первообразных функций.
Основной
задачей интегрального исчисления
является нахождение первообразной,
т.е. по данной функции f(x) найти такую
F(x), производная которой
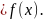
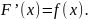
Функция F(x) называется ПЕРВООБРАЗНОЙ для функции на интервале (a;b), если для всех значений х из инт. (a;b) выполняется равенство: F’(x)=f(x).
ТЕОРЕМА. Если F(x)-первообразная для f(x) на (a;b), то любая другая первообр. для f(x) на (a;b) может быть представлена в виде: F(x)+C.
ДОКАЗАТЕЛЬСТВО:
Пусть функция у(х)-первообразная для
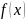 отличная от F(x). По определению
первообразной
отличная от F(x). По определению
первообразной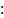
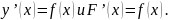
Вычтем
почленно эти равенства. Получим:
y’(x)-F’(x)=0. По правилу дифференцирования:
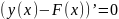
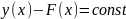

Т.е. каждая функция имеет бесконечное множество первообразных, одна из которых - F(x), а остальные F(x)+C.
27. Определение неопределенного интеграла. Теорема о существовании неопределенного интеграла (достаточное условие).
Если
функция
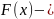 первообразная
для ф-ции
первообразная
для ф-ции
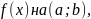 то
множество функций
то
множество функций
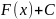 ,
где С произвольная постоянная, называется
НЕОПРЕДЕЛЕННЫМ ИНТЕГРАЛОМ функции
на этом интервале и обозначается
,
где С произвольная постоянная, называется
НЕОПРЕДЕЛЕННЫМ ИНТЕГРАЛОМ функции
на этом интервале и обозначается
 .
.
 подынтегральная
функция.
подынтегральная
функция.
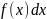 -
подынтегральное выражение.
-
подынтегральное выражение.
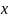 -
переменная интегрирования.
-
переменная интегрирования.
ТЕОРЕМА: Всякая непрерывная на интервале [a;b] функция имеет на этом интервале первообразную, а следовательно и неопределенный интеграл.
28. Таблица интегралов.
29. Свойства неопределенного интеграла.
1)
производная неопределенного интеграла = подынтегральной функции
дифференциал неопределенного интеграла = подынтегральному выражению
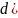
ДОКАЗАТЕЛЬСТВО. 1)
2)
, т.к.
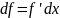
2)
неопределенный интеграл от дифференциала
некоторой функции = сумме этой функции
т произвольной константы
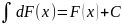
ДОКАЗАТЕЛЬСТВО.
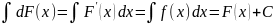 (по
определению неопределенного интеграла)
(по
определению неопределенного интеграла)
3)
Постоянный множитель можно вынести за
знак неопределенного интеграла

ДОКАЗАТЕЛЬСТВО.

4)неопределенный
интеграл от алгебраической суммы 2х
функций = алгебраической сумме интегралов
от этих функций
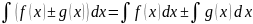
ДОКАЗАТЕЛЬСТВО.
 –
данное
свойство справедливо для любого
конечного числа слагаемых.
–
данное
свойство справедливо для любого
конечного числа слагаемых.
