42. Однородные дифференциальные уравнения.

Функция f(x;y) называется ОДНОРОДНОЙ n-ГО ПОРЯДКА если при умножении каждого её аргумента на произвольный множитель , вся функция умножается на .

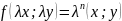
Дифференциальное уравнение называется ОДНОРОДНЫМ если функция f(x;y) есть однородная функция нулевого порядка, т.е. = f(x;y)

Дифференциальное уравнение 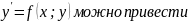к виду 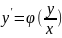т.к. функция 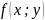однородная функция нулевого порядка, то 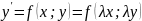положим что 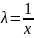тогда

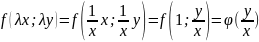
Уравнение можно привести к уравнению с разделяющимися переменными при помощи замены

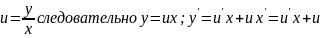
Подставим в :

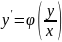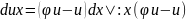
+C

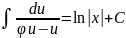-после интегрирования следует вернуться к замене, тогда получим общий интеграл исходного уравнения.

Однородные уравнения часто задаются в диф-ой форме 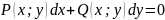Это уравнение будет однородным есл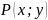и и 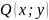- однородные функции одинакового порядка. Тогда это уравнение можно привести к виду

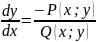
Потом интегрируем уравнение как указано выше. Заметим, что при интегрировании уравнения диф-ой формы нет необходимости приводить его к виду . Замена переменой 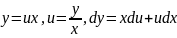сразу преобразует его в уравнение с разделяющимися переменными.

43. Линейные уравнения I-порядка.

Дифференциальное уравнение первого порядка называется линейным если его можно записать в ви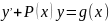де , где 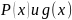некие заданные функции, в частности могут быть постоянными.

Особенность этого дифференциального уравнения: искомая функция y и её производная входят в уравнение первой степени не перемножаясь.

Способы интегрирования.

1) Метод Бернули. Решение уравнения 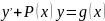ищется в виде произведения двух других функций, т.е. с помощью замены 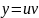, , 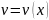следовательно

(**)

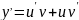
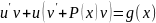Т.к. искомая функция ищется в виде произведения двух множителей, то один из этих множителей мы можем выбрать произвольно, а второй подобрать так, чтобы их произведение являлось искомой функцией. Поэтому выберем множитель v таким, чтобы - уравнение с разделенными переменными.

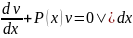
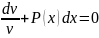
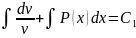
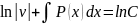, выберем произвольным образом C=1

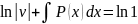
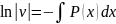
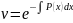
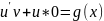(из**)

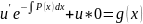приведем его к уравнению с разделяющимися переменными|:

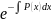
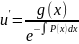
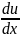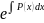= g(x) |*dx

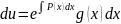далее интегрируем

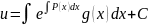
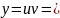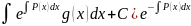( – ОБЩИЙ ИНТЕГРАЛ УРАВНЕНИЯ

2) Метод Лагранжа(метод вариации произвольной постоянной)

Этот метод состоит в том, чтобы сначала интегрировать уравнение из правой часть, т.е. уравнение вида 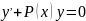. Оно называется линейное однородное дифференцированное уравнение первого порядка. В этом уравнении можно разделить переменные.

|dx

|:y

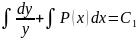
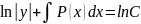
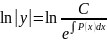
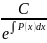= - решение соответствующего однородного уравнения.

Для того чтобы найти решение исходного уравнения будем полагать, что С- некая функция от х, которую необходимо найти, т.е. решение исходного уравнения ищем в виде:

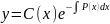, где С(х) – неизвестная функция

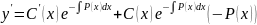
Подставим в :

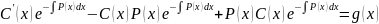
уравнение с разделяющимися переменными

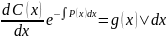
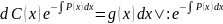
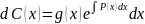И т.к.

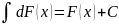
Следовательно

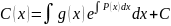
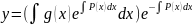
ЗАМЕЧАНИЕ. уравнение вида , где 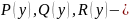заданные функции неравные 0 можно свести к линейному, если х считать функцией, а у – переменной, т.е. х=х(у) тогда, используя теорему о производной обратной функции

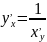
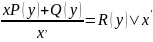
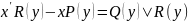
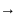такое уравнение решаем методом Бернули

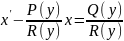т.е. получили линейное уравнение 1ой степени относительно y