37. Метод интегрирования по частям в определенном интеграле.
ТЕОРЕМА.
Если функции
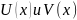имеют непрерывные производные на
,
то справедлива формула:
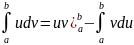
ДОКАЗАТЕЛЬСТВО.
Т.к. функции
на
имеют непрерывные производные, то
справедливо (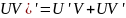
,
значит UV
- первообразные для
.
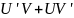Следовательно,
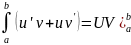
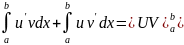
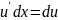и
,
т.к.
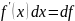
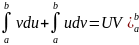
38. Определение несобственного интеграла первого рода (по бесконечному промежутку).
Пусть
функция
определена на промеж. [a;+∞] и интегрируема
при любом
,
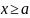существует
, где
.
Тогда, если существует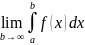
,
то его называют НЕСОБСТВЕННЫМ ИНТЕГРАЛОМ
1-ОГО РОДА и обозначают:
.
Таким образом, если предел в правой части сущ. И конечен, то говорят, что интеграл конечен и сходится. Если же предел не сущ. Или бесконечен, то интеграл не сущ. Или расходится.
Аналогично
вводится интеграл на (-∞;b]:
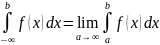
Для интеграла с обоими бесконечными пределами справедливо:
39. Определение несобственного интеграла второго рода (от функций, имеющих разрыв).
Пусть
функция f(x)
непрерывна на [a;b)
и имеет при х=b
бесконечный разрыв, тогда если существует
конечный предел
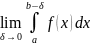, то его называют НЕСОБСТВЕННЫМ ИНТЕГРАЛОМ
2-ОГО РОДА и обозначают:
.
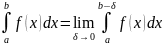Данный интеграл сходится, если предел, стоящий в правой части, существует и конечен. Если же предел не сущ. Или бесконечен, то говорят, что интеграл расходится.
Аналогично, если функция терпит разрыв в точке х=а
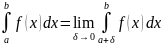
Если
функция терпит разрыв во внутренней
точке С отрезка [a;b],
то несобственный интеграл 2-ого рода
определяется формулой:
.
Такой интеграл сходится если сходятся оба несобственных интеграла в правой части.
40. Понятие о дифференциальных уравнениях. Общее и частное решение. Начальные условия. Задачи Коши.
41. Дифференциальные уравнения с разделяющимися переменными и метод их решения.
Уравнение
вида
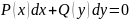наиболее простое дифференциальное
уравнение 1го порядка. В этом уравнении
одно слагаемое зависит только от х, а
другое только от у. Их называют уравнениями
с разделенными переменными. Чтобы найти
решение уравнения: проинтегрируем его
по членно.
+
;
+
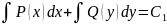
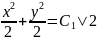
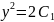общий
интеграл уравнения
-
общее решение
Более
общий случай описывают уравнения с
разделяющимися переменными. Это
уравнения вида:
=0
Особенностью этого уравнения является то, что коэфециенты при dx и dy представлены произведением 2х функций, каждая из которых зависит только от х или только от у.
Для решения такое уравнение сводится к уравнению с разделенными переменными.
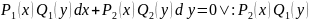
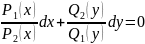
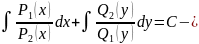общий
интеграл
ЗАМЕЧАНИЕ.
При проведении деления для уравнения
на
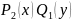могут быть поделены некоторые решения,
поэтому следует отдельно решить ур-ие
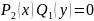и найти те решения, кот. могут быть
получены из общего решения. Такие
решения называются особыми.