
- •1. Действующее и среднее значение периодических напряжений и токов.
- •2. Коэффициенты, характеризующие форму несинусоидальных периодических кривых.
- •3. Порядок расчета цепи несинусоидального тока.
- •4. Показания приборов (амперметров, вольтметров, ваттметров) в цепи несинусоидального тока.
- •5. Зависимость формы кривой тока от характера цепи при несинусоидальном периодическом напряжении.
- •6. Резонансные явления при несинусоидальных периодических токах и напряжениях.
- •7. Мощность в цепях при несинусоидальных периодических токах и напряжениях.
- •8. Несинусоидальные периодические токи и напряжения в трехфазных цепях. Соединение фаз источника питания звездой и треугольником. Связь фазных и линейных напряжений.
- •9. Высшие гармоники в трехфазных цепях. Линейные токи и ток в нейтральном проводе.
- •10. Общий случай расчета переходных процессов классическим методом.
- •11. Законы коммутации, независимые и зависимые начальные условия.
- •12. Включение цепи r,l на постоянное и синусоидальное напряжение.
- •13. Включение цепи r,с на постоянное и синусоидальное напряжение.
- •14. Включение цепи r,l,с на постоянное напряжение.
- •15. Расчёт переходных процессов классическим методом. Составление характеристического уравнения.
- •16. Характер переходного процесса и корни характеристического уравнения. Определения постоянных интегрирования.
- •17.Переходной процесс в неразветвленной r,l,c цепи (корни вещественные, различные). График тока и напряжения на емкостном элементе.
- •18. Переходной процесс в неразветвленной r,l,c цепи (корни комплексно-сопряжённые). График тока и напряжения на емкостном элементе.
- •19. Предельно-апериодическая разрядка конденсатора. Графики зависимости тока и напряжения в индуктивном элементе. Напряжения на емкостном элементе.
- •20. Расчёт переходных процессов операторным методом. Законы Ома и Кирхгофа в операторной форме. Эквивалентная операторная схема и её расчет.
- •21. Эквивалентная операторная схема. Расчет полного решения переходного тока или напряжения и преходящей составляющей.
- •22. Определение оригинала по изображению. Теорема разложения.
- •2 4. Переходные процессы при «некорректных» коммутациях.
- •25. Расчет переходных процессов методом дискретных схем замещения.
- •26. Расчет переходных процессов методом переменных состояния.
- •27. Формирование уравнений состояния в методе переменных состояния.
- •28. Сравнение методов расчета переходных процессов в линейных электрических цепях.
- •29. Четырехполюсники их основные уравнения. Активные, автономные и неавтономные четырехполюсники. Взаимные и невзаимные, симметричные и несимметричные четырехполюсники.
- •30. Эквивалентные схемы замещения четырехполюсников.
- •31. Определение первичных параметров несимметричного четырехполюсника из режима хх и кз.
- •32. Определение входного сопротивления четырехполюсника из режима хх и кз, при произвольной нагрузки.
- •35.Соединение четырехполюсников: каскадное, последовательное и параллельное. Вторичные параметры при каскадном соединении четырехполюсников.
- •36. Частотные электрические фильтры. Классификация. Полосы пропускания и ослабления (задержки). Граничные частоты.
- •37. Низкочастотные фильтры типа «к».Первичные и вторичные параметры. Т-образная схема замещения. Частотные характеристики в режиме согласованной нагрузки.
- •38. Высокочастотные фильтры типа «к». Первичные и вторичные параметры. Т-образная схема замещения. Частотные характеристики в режиме согласованной нагрузки.
- •39. Низкочастотные фильтры типа «к». Первичные и вторичные параметры. П-образная схема замещения. Частотные характеристики в режиме согласованной нагрузки.
- •40. Высокочастотные фильтры типа «к». Первичные и вторичные параметры. П-образная схема замещения. Частотные характеристики в режиме согласованной нагрузки.
22. Определение оригинала по изображению. Теорема разложения.
Для перехода от изображения искомой функции F(p) к ее оригиналу f(t) можно использовать следующие три способа:
1. Непосредственное нахождение f(t) по таблице соответствия оригиналов и изображений.
2. Представление рациональной дроби изображения
![]()
в
случае n > m и различия всех корней pj,
j=1,2,…n полинома F2(p)
в виде
![]() где
Aj
— так называемые неопределенные
коэффициенты. При этом искомая функция
оригинал будет иметь вид f(t)=A1*ep1t
+ A2ep2t
+ … + An*epnt.
где
Aj
— так называемые неопределенные
коэффициенты. При этом искомая функция
оригинал будет иметь вид f(t)=A1*ep1t
+ A2ep2t
+ … + An*epnt.
3. Использование теоремы разложения. Находим корни полинома F2(p)=0.
Если все корни pj полинома F2(p) вещественные различные, то оригинал изображения F(p) имеет вид:
![]()
![]()
где
Если при этом один из корней F2(p), равен нулю, т.е. F2(p)=рF3(p) (для определенности первый р1=0), то
![]()
Если F2(p) имеет n/2 пар комплексно-сопряженных корней (здесь n — четное число), то
![]()
При наличии нулевого корня, т.е. F2(p) = рF3(p), .
![]()
В случае если корни полинома кратные (равные), формула разложения усложняется. В таком случае решение можно получить, сводя полученное изображение к табличным.
2 4. Переходные процессы при «некорректных» коммутациях.
Пусть в момент t = 0 происходит размыкание ключа.
После коммутации составим уравнение по второму закону Кирхгофа:
![]() , закон
изменения переходного тока определим
классическим методом
, закон
изменения переходного тока определим
классическим методом
![]() .
Для определения
постоянной интегрирования А необходимо
определить значение тока в момент t =
0+. По законам коммутации для тока в
индуктивном элементе i(0–)
= i(0+).
До коммутации ток в первой катушке. При
этом ток до коммутации во второй катушке
был равен нулю iL2(0–)
= 0 = iL2(0+).
Но вследствие последовательного
соединения катушек после коммутации
i(0+)
= iL1(0+)
= iL2(0+),
при этом iL1(0+)
≠ iL2(0+).
Противоречие! Токи в первой и второй
катушках изменились скачкообразно, что
привело к появлению «бесконечно» больших
напряжений на этих элементах.
Так как приложенное напряжение источника
э.д.с. E конечно, конечными являются и
напряжения на резисторах R1
и R2,
следовательно, конечной должна быть и
сумма напряжений на катушках. В малый
промежуток времени, когда происходит
коммутация, т.е. 0– ≤ t ≤ 0+ при скачкообразном
изменении токов в катушках это условие
может выполняться, только если uL1(0–
≤ t ≤ 0+)
= –uL2(0–
≤ t ≤ 0+)
или
.
Для определения
постоянной интегрирования А необходимо
определить значение тока в момент t =
0+. По законам коммутации для тока в
индуктивном элементе i(0–)
= i(0+).
До коммутации ток в первой катушке. При
этом ток до коммутации во второй катушке
был равен нулю iL2(0–)
= 0 = iL2(0+).
Но вследствие последовательного
соединения катушек после коммутации
i(0+)
= iL1(0+)
= iL2(0+),
при этом iL1(0+)
≠ iL2(0+).
Противоречие! Токи в первой и второй
катушках изменились скачкообразно, что
привело к появлению «бесконечно» больших
напряжений на этих элементах.
Так как приложенное напряжение источника
э.д.с. E конечно, конечными являются и
напряжения на резисторах R1
и R2,
следовательно, конечной должна быть и
сумма напряжений на катушках. В малый
промежуток времени, когда происходит
коммутация, т.е. 0– ≤ t ≤ 0+ при скачкообразном
изменении токов в катушках это условие
может выполняться, только если uL1(0–
≤ t ≤ 0+)
= –uL2(0–
≤ t ≤ 0+)
или
![]() .
Проинтегрируем это выражение:
.
Проинтегрируем это выражение:
![]() или
или
![]() .
.
Тогда
L1[iL1(0+)
– iL1(0–)]
= – L2[iL2(0+)
– iL2(0–)],
![]() .
.
Для
нашей задачи
![]() .
Можно определить постоянную интегрирования
.
Можно определить постоянную интегрирования
![]() .
При этом использовался обобщенный закон
коммутации для потокосцеплений: для
любого замкнутого контура суммарное
потокосцепление после коммутации (t =
0+)
равно сумме потокосцеплений до коммутации
(t = 0–)
всех входящих в контур катушек ∑Ψ(0–)
= ∑Ψ(0+).
При этом катушки могут входить в замкнутый
контур только после коммутации.
.
При этом использовался обобщенный закон
коммутации для потокосцеплений: для
любого замкнутого контура суммарное
потокосцепление после коммутации (t =
0+)
равно сумме потокосцеплений до коммутации
(t = 0–)
всех входящих в контур катушек ∑Ψ(0–)
= ∑Ψ(0+).
При этом катушки могут входить в замкнутый
контур только после коммутации.
25. Расчет переходных процессов методом дискретных схем замещения.
Р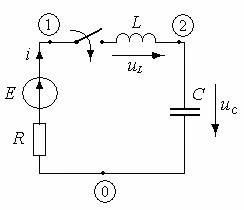 ассчитать
переходной процесс с использованием
дискретных схем замещения.
ассчитать
переходной процесс с использованием
дискретных схем замещения.
Обозначим
![]() ,
,![]() .
Выберем шаг интегрирования h. Рассчитаем
.
Выберем шаг интегрирования h. Рассчитаем
![]() и
и
![]() .
.
С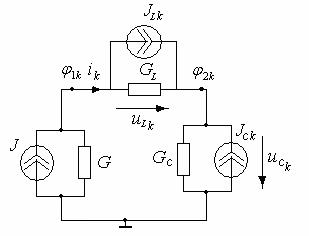 оставим
резистивную схему для расчета k-ой
итерации. При нулевых начальных условиях
JL0
= iL0
= iL(0)
= 0,
оставим
резистивную схему для расчета k-ой
итерации. При нулевых начальных условиях
JL0
= iL0
= iL(0)
= 0,
![]() .
.
По методу узловых потенциалов на k-ой итерации рассчитаем φ1k и φ2k:
![]() .
.
Для тока и напряжений на реактивных элементах на k-ой итерации:
ik = JLk + GL·(φ1k – φ2k),
uCk = φ2k, uLk = φ1k – φ2k.
