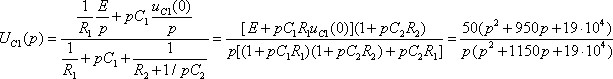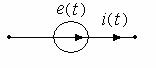- •1. Действующее и среднее значение периодических напряжений и токов.
- •2. Коэффициенты, характеризующие форму несинусоидальных периодических кривых.
- •3. Порядок расчета цепи несинусоидального тока.
- •4. Показания приборов (амперметров, вольтметров, ваттметров) в цепи несинусоидального тока.
- •5. Зависимость формы кривой тока от характера цепи при несинусоидальном периодическом напряжении.
- •6. Резонансные явления при несинусоидальных периодических токах и напряжениях.
- •7. Мощность в цепях при несинусоидальных периодических токах и напряжениях.
- •8. Несинусоидальные периодические токи и напряжения в трехфазных цепях. Соединение фаз источника питания звездой и треугольником. Связь фазных и линейных напряжений.
- •9. Высшие гармоники в трехфазных цепях. Линейные токи и ток в нейтральном проводе.
- •10. Общий случай расчета переходных процессов классическим методом.
- •11. Законы коммутации, независимые и зависимые начальные условия.
- •12. Включение цепи r,l на постоянное и синусоидальное напряжение.
- •13. Включение цепи r,с на постоянное и синусоидальное напряжение.
- •14. Включение цепи r,l,с на постоянное напряжение.
- •15. Расчёт переходных процессов классическим методом. Составление характеристического уравнения.
- •16. Характер переходного процесса и корни характеристического уравнения. Определения постоянных интегрирования.
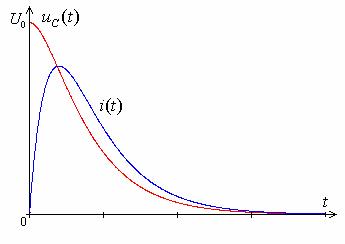
- •17.Переходной процесс в неразветвленной r,l,c цепи (корни вещественные, различные). График тока и напряжения на емкостном элементе.
- •18. Переходной процесс в неразветвленной r,l,c цепи (корни комплексно-сопряжённые). График тока и напряжения на емкостном элементе.
- •19. Предельно-апериодическая разрядка конденсатора. Графики зависимости тока и напряжения в индуктивном элементе. Напряжения на емкостном элементе.
- •20. Расчёт переходных процессов операторным методом. Законы Ома и Кирхгофа в операторной форме. Эквивалентная операторная схема и её расчет.
- •21. Эквивалентная операторная схема. Расчет полного решения переходного тока или напряжения и преходящей составляющей.
- •22. Определение оригинала по изображению. Теорема разложения.
- •2 4. Переходные процессы при «некорректных» коммутациях.
- •25. Расчет переходных процессов методом дискретных схем замещения.
- •26. Расчет переходных процессов методом переменных состояния.
- •27. Формирование уравнений состояния в методе переменных состояния.
- •28. Сравнение методов расчета переходных процессов в линейных электрических цепях.
- •29. Четырехполюсники их основные уравнения. Активные, автономные и неавтономные четырехполюсники. Взаимные и невзаимные, симметричные и несимметричные четырехполюсники.
- •30. Эквивалентные схемы замещения четырехполюсников.
- •31. Определение первичных параметров несимметричного четырехполюсника из режима хх и кз.
- •32. Определение входного сопротивления четырехполюсника из режима хх и кз, при произвольной нагрузки.
- •35.Соединение четырехполюсников: каскадное, последовательное и параллельное. Вторичные параметры при каскадном соединении четырехполюсников.
- •36. Частотные электрические фильтры. Классификация. Полосы пропускания и ослабления (задержки). Граничные частоты.
- •37. Низкочастотные фильтры типа «к».Первичные и вторичные параметры. Т-образная схема замещения. Частотные характеристики в режиме согласованной нагрузки.
- •38. Высокочастотные фильтры типа «к». Первичные и вторичные параметры. Т-образная схема замещения. Частотные характеристики в режиме согласованной нагрузки.
- •39. Низкочастотные фильтры типа «к». Первичные и вторичные параметры. П-образная схема замещения. Частотные характеристики в режиме согласованной нагрузки.
- •40. Высокочастотные фильтры типа «к». Первичные и вторичные параметры. П-образная схема замещения. Частотные характеристики в режиме согласованной нагрузки.
17.Переходной процесс в неразветвленной r,l,c цепи (корни вещественные, различные). График тока и напряжения на емкостном элементе.
Пусть в цепи конденсатор был заряжен до напряжения uc(0-)=U0. Исследуем переходной процесс после замыкания в момент t=0 ключа.
1). ННУ uc(0+)=uc(0- )=U0, i(0-)=i(0+)=0
2 ).
Так как источники в цепи отсутствуют,
то
).
Так как источники в цепи отсутствуют,
то
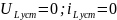 .
.
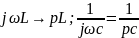 ;
3).
;
3).
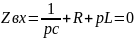
![]()
4).
При апериодическом разряде конденсатора,
т.е. при условии
![]() или
или
![]() решение имеет вид:
решение имеет вид:
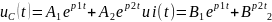
5).
Определим из начальных условий постоянные
интегрирования. Так как uC(0+)=U0
и
![]() для определения постоянных интегрирования
при апериодическом разряде решаем
уравнения
для определения постоянных интегрирования
при апериодическом разряде решаем
уравнения
![]()
![]()
![]()
Для
тока i(0+)=0,
напряжение на катушке как зависимое
начальное условие найдем по второму
закону Кирхгофа. Для момента t=0+
U0=i(0+)R+uL(0+).
Следовательно
![]() .
Тогда B1
и B2
.
Тогда B1
и B2
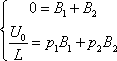
Решение переходного процесса имеет вид: для апериодического разряда
![]()
![]()
18. Переходной процесс в неразветвленной r,l,c цепи (корни комплексно-сопряжённые). График тока и напряжения на емкостном элементе.
1 ). ННУ uc(0+)=uc(0- )=Uо, i(0- )=i(0+)=0.
2). Так как источники в цепи отсутствуют, то .
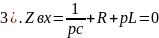 ;
;


4.
При
периодическом разряде конденсатора![]() решение имеет вид:
решение имеет вид:
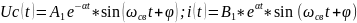
5. Уравнения для нахождения постоянных интегрирования:
Uo=Asinϕ; 0=-αAsinϕ+ωсвAcosϕ
 ;
;

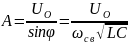 ;
;
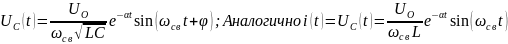
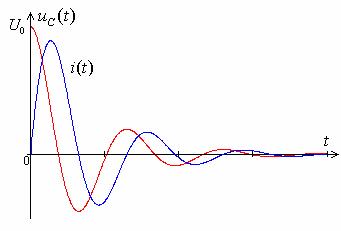
19. Предельно-апериодическая разрядка конденсатора. Графики зависимости тока и напряжения в индуктивном элементе. Напряжения на емкостном элементе.
1 ). ННУ: uc(0+)=uc(0- )=Uо, i(0- )=i(0+)=0.
2).
Так как источники в цепи отсутствуют,
то

3).
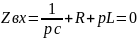 ;
D=0;
;
D=0;

4).
В случае предельно-апериодического
разряда при
![]() корни p1=p2=-R/(2L)=-α,
решение:
корни p1=p2=-R/(2L)=-α,
решение:
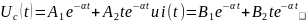
5). Находим постоянные интегрирования:

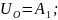
 ->
->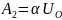 ;
;
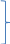
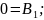
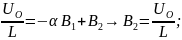
![]()

![]()
20. Расчёт переходных процессов операторным методом. Законы Ома и Кирхгофа в операторной форме. Эквивалентная операторная схема и её расчет.
Вместо
описания во временной области используют
описание уравнениями в операторной
области (области изображений Лапласа).
Каждой функции времени f(t) , называемой
оригиналом, ставится в соответствие
операторное изображение F(p) , где p -
некоторое комплексное число. Первый
закон Кирхгофа:
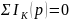 .
Второй закон Кирхгофа:
.
Второй закон Кирхгофа:
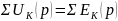 .
.
Временная область |
Операторная область |
|
|
|
|
|
|
|
|
|
|
1. Рассчитывается режим в цепи до коммутации. t=0
2. Составляется операторная схема.
3. Находятся операторные токи и напряжения искомых элементов.
4. По найденным изображениям находятся оригиналы во временной обл.
21. Эквивалентная операторная схема. Расчет полного решения переходного тока или напряжения и преходящей составляющей.
Дано: e(t) = Em*sin(ωt + ψ), параметры элементов R1, R, L и С.
Р
 ешение:
Операторная схема для полного решения:
ешение:
Операторная схема для полного решения:
![]() .
.
Изображение E(p) достаточно громоздкое, что затруднит переход от найденного изображения IL(p) к оригиналу. Поэтому по схеме до коммутации определим iL(0), используя комплексный метод расчета. По схеме установившегося режима после коммутации рассчитаем iLуст(0).
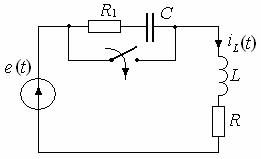
Начальные условия по преходящей составляющей:
iLпрех(0) = iL(0) – iLуст(0).
О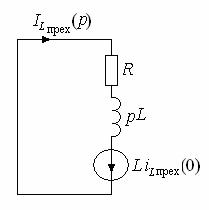 ператорная
схема для преходящей составляющей:
ператорная
схема для преходящей составляющей:
![]()

Найти операторное изображение UC1(p).
Решение: Составим эквивалентную операторную схему цепи после коммутации, начальные условия: uC1(0+) = uC1(0–) = 50 B, uC2(0+) = uC2(0–) = 0.
Применим формулу двух узлов для нахождения искомого изображения: