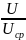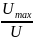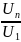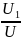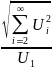- •1. Действующее и среднее значение периодических напряжений и токов.
- •2. Коэффициенты, характеризующие форму несинусоидальных периодических кривых.
- •3. Порядок расчета цепи несинусоидального тока.
- •4. Показания приборов (амперметров, вольтметров, ваттметров) в цепи несинусоидального тока.
- •5. Зависимость формы кривой тока от характера цепи при несинусоидальном периодическом напряжении.
- •6. Резонансные явления при несинусоидальных периодических токах и напряжениях.
- •7. Мощность в цепях при несинусоидальных периодических токах и напряжениях.
- •8. Несинусоидальные периодические токи и напряжения в трехфазных цепях. Соединение фаз источника питания звездой и треугольником. Связь фазных и линейных напряжений.
- •9. Высшие гармоники в трехфазных цепях. Линейные токи и ток в нейтральном проводе.
- •10. Общий случай расчета переходных процессов классическим методом.
- •11. Законы коммутации, независимые и зависимые начальные условия.
- •12. Включение цепи r,l на постоянное и синусоидальное напряжение.
- •13. Включение цепи r,с на постоянное и синусоидальное напряжение.
- •14. Включение цепи r,l,с на постоянное напряжение.
- •15. Расчёт переходных процессов классическим методом. Составление характеристического уравнения.
- •16. Характер переходного процесса и корни характеристического уравнения. Определения постоянных интегрирования.
- •17.Переходной процесс в неразветвленной r,l,c цепи (корни вещественные, различные). График тока и напряжения на емкостном элементе.
- •18. Переходной процесс в неразветвленной r,l,c цепи (корни комплексно-сопряжённые). График тока и напряжения на емкостном элементе.
- •19. Предельно-апериодическая разрядка конденсатора. Графики зависимости тока и напряжения в индуктивном элементе. Напряжения на емкостном элементе.
- •20. Расчёт переходных процессов операторным методом. Законы Ома и Кирхгофа в операторной форме. Эквивалентная операторная схема и её расчет.
- •21. Эквивалентная операторная схема. Расчет полного решения переходного тока или напряжения и преходящей составляющей.
- •22. Определение оригинала по изображению. Теорема разложения.
- •2 4. Переходные процессы при «некорректных» коммутациях.
- •25. Расчет переходных процессов методом дискретных схем замещения.
- •26. Расчет переходных процессов методом переменных состояния.
- •27. Формирование уравнений состояния в методе переменных состояния.
- •28. Сравнение методов расчета переходных процессов в линейных электрических цепях.
- •29. Четырехполюсники их основные уравнения. Активные, автономные и неавтономные четырехполюсники. Взаимные и невзаимные, симметричные и несимметричные четырехполюсники.
- •30. Эквивалентные схемы замещения четырехполюсников.
- •31. Определение первичных параметров несимметричного четырехполюсника из режима хх и кз.
- •32. Определение входного сопротивления четырехполюсника из режима хх и кз, при произвольной нагрузки.
- •35.Соединение четырехполюсников: каскадное, последовательное и параллельное. Вторичные параметры при каскадном соединении четырехполюсников.
- •36. Частотные электрические фильтры. Классификация. Полосы пропускания и ослабления (задержки). Граничные частоты.
- •37. Низкочастотные фильтры типа «к».Первичные и вторичные параметры. Т-образная схема замещения. Частотные характеристики в режиме согласованной нагрузки.
- •38. Высокочастотные фильтры типа «к». Первичные и вторичные параметры. Т-образная схема замещения. Частотные характеристики в режиме согласованной нагрузки.
- •39. Низкочастотные фильтры типа «к». Первичные и вторичные параметры. П-образная схема замещения. Частотные характеристики в режиме согласованной нагрузки.
- •40. Высокочастотные фильтры типа «к». Первичные и вторичные параметры. П-образная схема замещения. Частотные характеристики в режиме согласованной нагрузки.
1. Действующее и среднее значение периодических напряжений и токов.
Периодический ток, напряжение, ЭДС принято характеризовать со следующими значениями:
максимальным значением тока Imax, напряжения Umax, ЭДС Emax;
действующим значением тока I, напряжения U, ЕДС E, где
![]()
![]()
![]()
средним по модулю значением тока Iср, напряжения Uср, ЭДС Eср :
![]()
![]()
![]()
2. Коэффициенты, характеризующие форму несинусоидальных периодических кривых.
Формы периодических несинусоидальных кривых токов, напряжений, ЭДС принято оценивать специальными коэффициентами. В Таблице такие коэффициенты даны применительно к периодическому напряжению u(t).
Название коэффициента |
Обозначение |
Выражение |
Коэффициент формы |
kф |
|
Коэффициент амплитуды |
kа |
|
Коэффициент n-й гармоники n > 2 |
kn |
|
Коэффициент искажения |
kи |
|
Коэффициент гармоник |
kг |
|
Эти коэффициенты позволяют оценить разные аспекта интенсивности, «несинусоидальности» рассматриваемых процессов, т. е. дают интегральные оценки качества процессов.
3. Порядок расчета цепи несинусоидального тока.
Представив все ЭДС и токи источников в виде рядов Фурье, можно затем произвести расчет цепи отдельно по каждой из гармоник — по нулевой гармонике (постоянному току), когда ЭДС и токи источников тока учитываются только их постоянными составляющими, по первой гармонике, когда источники считаются синусоидальными с частотой ω и т.д. В результате определяются постоянная и гармонические составляющие токов и напряжений цепи, которые затем в соответствии с принципом суперпозиции суммируются. Так, для некоторого тока имеем
i(t)=I0+i(1)+i(2)+...+i(k)+...= I0+i(1)+i(2)+...+i(N),
где I0 — постоянная, а i(k), k > 1 — гармонические составляющие тока i(k)(t)=I0sin(kωt+φk), N — номер гармоники тока, обеспечивающий требуемую точность его вычисления. Расчет первой и высших гармоник удобно проводить комплексным методом, при этом обязательно переводя его результат в вещественную (временную) область, т.к. суммировать гармоники можно только в этой области. В цепях с полигармоническим воздействием, когда ЭДС и токи источников имеют вид
![]() и
и ![]()
где ωk имеют необязательно целочисленные значения, комплексным методом рассчитываются режимы для каждой частоты ωk, а затем результаты расчетов суммируются в вещественной области. При этом исключается операция разложения e(t) и J(t) в ряд Фурье.
При использовании комплексного метода необходимо пересчитывать комплексные сопротивления индуктивного XL(k)=kωL=kXL(1) и емкостного XC(k)=1/kωC=XC(1)/k элементов для каждой гармоники k = 1,2,…N. Таким образом, сопротивление резистора принимается независящим от номера гармоники, индуктивное сопротивление растет по величине пропорционально номеру k, а емкостное уменьшается обратно пропорционально.
4. Показания приборов (амперметров, вольтметров, ваттметров) в цепи несинусоидального тока.
В зависимости от исполнения прибора (вольтметра или амперметра) и устройства его входного преобразователя он может показывать действующее значение измеряемой величины, ее среднее по модулю значение, усредненным за период положительным (отрицательным) значением и т.д.
Магнитоэлектрические приборы показывают постоянную составляющую измеряемой величины, электромагнитные, электродинамические, электростатические и тепловые — ее действующее значение. Показания электронных приборов в зависимости от устройства входного преобразователя могут определяться действующим значением измеряемой величины, средним по модулю, максимальным или минимальным значением измеряемой величины. Прибор индукционной системы и электронный прибор с конденсатором на входе определяет действующее значение переменной составляющей измеряемой величины.