Алгоритм построения минимального каркаса

Пусть G(X,E) - связный нагруженный граф сpвершинами.

Шаг 1. В качестве первого ребра искомого минимального каркаса выбираем реброe₁с наименьшим весом(e₁). Если таких ребер несколько, то берем любое из них.

Шаг 2. В качестве второго ребра берем реброe₂из множестваE\{e₁}, имеющее наименьший вес(e₂), и такое, что множество {e₁,e₂} не содержит простых циклов. Если таких ребер несколько, то берем любое из них.

Шаг 3. В качестве третьего ребра выбираем такое реброe₃из множестваE\{e₁,e₂}, которое имеет наименьший вес(e₂) и для которого множество {e₁,e₂,e₃} не содержит простых циклов. Если таких ребер несколько, берем любое из них.

Указанный процесс повторяется и через некоторое число kшагов дает множество E = {e₁,e₂, …,e_k}, к которому нельзя добавить ребро без появления цикла. ПодграфG₁(X,E₁) и является минимальным каркасом графаG(X,E).

Обоснование алгоритма

В силу свойства 6из теоремы 6.1 построенный подграфG₁(X,E₁) является деревом, поэтомуk=p–1. Доказательство минимальности каркасаG₁(X,E₁) разобьем на два этапа. Пусть сначалаG(X,E) – полный граф, у которого веса всех ребер различны, и пустьG₂(X,E₂) – минимальный каркас графаG. ЕслиE₂E₁, то рассмотримe_l– первое из ребер множестваE₁, не принадлежащееE₂. В графев силу свойства 6теоремы 6.1 существует единственный простой цикл. Циклсодержит реброe₀E₁. ГрафG₃(X,E₃), где, не содержит циклов и имеетn– 1 ребро, поэтому он является деревом. Множество {e₁,e₂, …,e_l-1,e₀} содержится вE₂и поэтому не содержит циклов. Тогда в силу рассмотренного выше алгоритма(e₀) >(e_l). Отсюда следует, что суммарный вес дереваG₃(X,E₃) меньше веса дереваG₂(X,E₂). Это противоречит минимальности каркасаG₂, поэтомуE₂=E₁иG₁(X,E₁) – единственный минимальный каркас графаG.

Пусть теперь G(X,E) – произвольный нагруженный связный граф. Если(e₁) =(e₂), то сделаем замену

(e₁)'(e₁) =(e₁) +,

(e₂)'(e₂) =(e₂) + 2,

взяв такое , чтобы сохранились соотношения весов(e₁) и(e₂) с другими весами. Сделаем графGполным, добавив такие ребраd_i, что. В полученном графе единственным минимальным каркасом будет каркас, полученный с помощью рассмотренного алгоритма. Легко видеть, что этот каркас будет минимальным и в исходном графеG(X,E).

На рис. 6.4 изображены нагруженный граф Gи его минимальный каркасG₁.

Рис. 6.4

7. Эйлеровы цепи и циклы

Рассматриваемая в этой главе задача является одной из самых ста­рей­ших в теории графов. В городе Кенигсберге (ныне Калининград) имелось семь мостов, соединяющих два берега реки Преголь, и два основа на ней друг с другом (рис. 7.1а). Требуется, начав путешествие из одной точки города прой­ти по всем мостам по одному разу и вернуться в исходную точку.

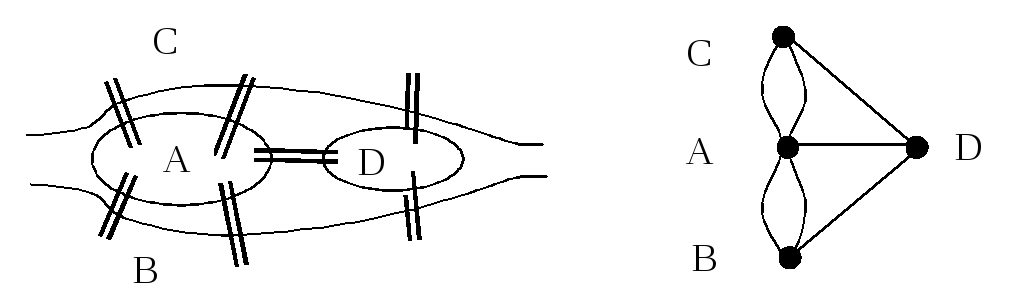
а) б)

Рис. 7.1.

Если поставить в соответствие мостам ребра, а участкам суши — вершины, то получится граф (точнее псевдограф), в котором надо найти про­стой цикл, проходящий через все ребра. В общем виде эта задача была решена Эйлером в 1736 г.

Дадим теперь

Определение 7.1.Эйлеровой цепьюв неориентированном графеGназы­ва­ется простая цепь, содержащая все ребра графаG.Эйлеровым цикломназы­вается замкнутая Эйлерова цепь. Аналогично,эйлеров путьв орграфеG— это простой путь, содержащий все дуги графаG.Эйлеров контурв орграфеG— это замкнутый эйлеров путь. Граф, в котором существует эйлеров цикл, называетсяэйлеровым.

Простой критерий существования эйлерова цикла в связном графе дается следующей теоремой.

Теорема 7.1.(Эйлер) Эйлеров цикл в связном неориентированном графеG(X,E) существует только тогда, когда все его вершины имеют четную степень.

Доказательство. Необходимость.Пусть- эйлеров цикл в связном гра­феG,x— произвольная вершина этого графа. Через вершинуxэйлеров цикл проходит некоторое количествоk(k1) раз, причем каждое прохождение, очевидно, включает два ребра, и степень этой вершины равна 2k, т.е. четна, так какxвыбрана произвольно, то все вершины в графеGимеют четную сте­пень.

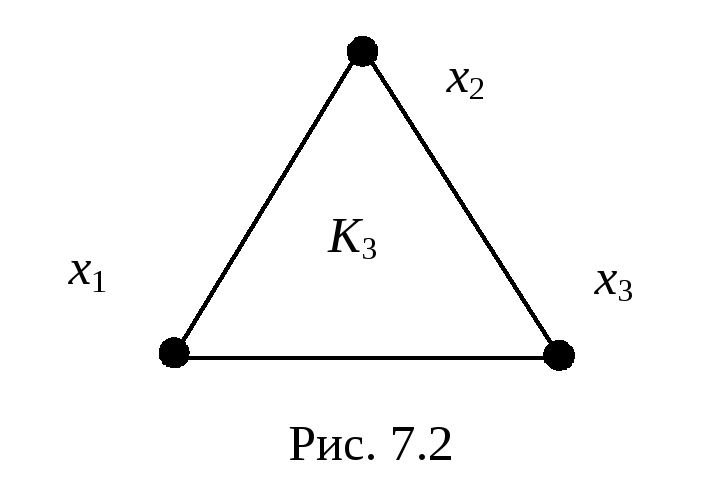
Достаточность.Воспользуемся индукцией по числуmребер графа. Эйле­ровы циклы для обычных (не псевдо) графов можно построить начиная сm=3.Легко проверить, что единственный граф сm=3, имеющий все вершины с четными степенями, есть графK₃(рис. 7.2). Существование эйлерова цикла в нем очевидно. Таким образом, дляm=3 достаточность условий доказываемой теоремы имеет место. Пусть теперь графGимеетm>3 ребер, и пусть утверждение справедливо для всех связных графов, имеющих меньше, чемmребер. Зафиксируем произвольную вершинуaграфаGи будем искать простой цикл, идущий изaвa. Пусть(a,x) — простая цепь, иду­щая изaв некоторую вершинуx. Еслиx a, то цепьможно продолжить из вершиныxв некотором направлении. Через некоторое число таких про­дол­­же­ний мы придем в вершинуzX, из которой нельзя продлить полу­чен­ную про­стую цепь. Легко видеть, чтоz =aтак как из всех остальных вершин цепь может выйти (четные степени!);aвaона начиналась. Таким образом, нами построен цикл, идущий изaвa. Предположим, что построенный про­стой цикл не содержит всех ребер графаG. Удалим ребра, входящие в цикл, из графаGи рассмотрим полученный граф. В графевсе вершины имеют четные степени. Пусть— компо­нен­ты связ­нос­ти графа, содержащие хотя бы по одному ребру. Соглас­но пред­поло­же­нию индукции все эти компоненты обладают эйлеровыми циклами₁,₁, …,_kсоот­вет­ствен­но. Так как графGсвязан, то цепьвстре­чает каждую из компонент. Пусть первые встречи циклас ком­понентамипроисходят соответственно в вершинахx₁,x₂, …,x_k. Тогда про­стая цепь

(a,a)=(a,x₁)₁(x₁,x₁)(x₁,x₂)…_k(x_k,x_k)(x_k,a)

является эйлеровым циклом в графе G. Теорема доказана.

Замечание.Очевидно, что приведенное доказательство будет верно и для псевдографов, содержащих петли и кратные ребра (см. рис. 7.1,а).

Таким образом, задача о кенигсбергских мостах не имеет ре­ше­ния, так как соответствующий граф (см. рис. 7.1,б) не имеет эйлерова цикла из-за не­четности степеней все вершин.

О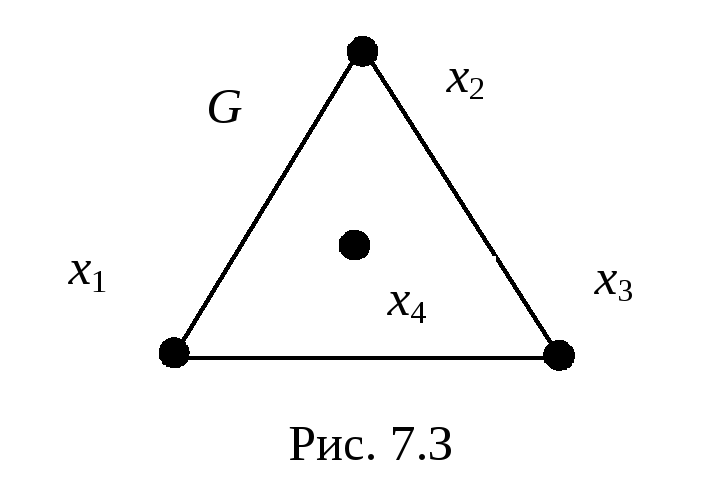тметим, что из существования эйле­ро­ва цикла в неориентированном графеGне следует связность этого графа. Напри­мер, неориентированный графGна рис. 7. 3 обладает эйлеровым циклом и вместе с тем несвязен.

Совершенно также, как теорема 7.1, могут быть доказаны следующие два утверждения.

Теорема 7.2.Связный неориентированный графGобладает эйлеровой цепью тогда и только тогда, когда число вершин нечетной степени в нем равно 0 или 2, причем если это число равно нулю, то эйлерова цепь будет являться и циклом.

Теорема 7.3.Сильно связный орграфG(X,E) обладает эйлеровым кон­ту­ром тогда и только тогда, когда для любой вершиныxXвыполняется

.

Можно также обобщить задачу, которую решал Эйлер следующим обра­зом. Будем говорить что множество не пересекающихся по ребрам простых цепей графаGпокрываетего, если все ребра графаGвключены в цепи_i. Нужно найти наименьшее количество таких цепей, которыми можно покрыть заданный графG.

Если граф G— эйлеров, то очевидно, что это число равно 1. Пусть теперьGне является эйлеровым графом. Обозначим черезkчисло его вер­шин нечетной степени. По теореме …kчетно. Очевидно, что каждая верши­на нечетной степени должна быть концом хотя бы одной из покрывающихGцепей_i. Следовательно, таких цепей будет не менее чемk/2. С другой сто­роны, таким количеством цепей графGпокрыть можно. Чтобы убедиться в этом, расширимGдо нового графа, добавивk/2 ребер, соединяющих раз­личные пары вершин нечетной степени. Тогдаоказывается эйлеровым графом и имеет эйлеров цикл. После удаления изреберграф разло­жится наk/2 цепей, покрывающихG. Таким образом, доказана

Теорема 7.4.ПустьG— связный граф сk>0 вершинами нечетной степени. Тогда минимальное число непересекающихся по ребрам простых цепей, покрывающихG, равноk/2.