5. Связные графы. Компонента связности

Расcмотрим неориентированный графG(X,E,). Конечная последовательность реберМ=e₁, e₂, . . . , e_kграфа называетсяцепью (маршрутом)длиныk, если существует такая последовательность вершин(x₀, x₁, . . . , х_k), что{e_i} = (x_i-1, x_i), гдеi = 1, 2, . . . , k. Вершиныx₀иx_kназываются соответственноначальной и конечнойвершинами маршрута, остальные вершины называютсявнутренними.Маршрутдлиныkможет записываться как в виде последовательности ребер = {e₁, e₂, . . . , e_k}, так и в виде последовательности вершин _{= {}x₀, x₁, . . . , x_k}.

Цепь  = {e₁, e₂, . . . , e_k}, в которой все ребра различны, называется простой. Цепь ₌ {x₀, x₁, . . . , x_k}, в которой все вершины различны, называется элементарной.

Пусть  = {e₁, e₂, . . . , e_k}— цепь в графеG; для некоторой последовательности номеровi₁, i₂, . . . , i_r, (гдеr 1, 1 i₁<i₂< ... <i_k) последовательность ребер (e_i1, e_i2, . . . ,e_ir) называетсяподцепьюцепи; при этом говорят, что цепь(e_i1, e_i2, . . . ,e_ir)выделенаиз цепи  = {e₁, e₂, . . . , e_k}.

Если цепь имеет начальную вершину, но не имеет конечной, или имеет конечную вершину, но не имеет начальной, то она называетсяодносторонне бесконечной.Если цепь не имеет ни начальной, ни конечной вершины, то она называетсядвусторонне бесконечной,замкнутой цепью, или циклом.Цепь называетсянетривиальной,если она содержит хотя бы одно ребро (дугу); для обеспечения общности рассуждений вводится понятиенуль – цепи, не содержащей никаких ребер (дуг). Цикл называетсяпростым, если все его ребра различны, и элементарным, если все вершины, через которые он проходит,различны.

Цепи и^|считаютсяравными,если они имеют одинаковую длину и состоят из одних и тех же ребер. В противном случае цепии^|считаются различными.

П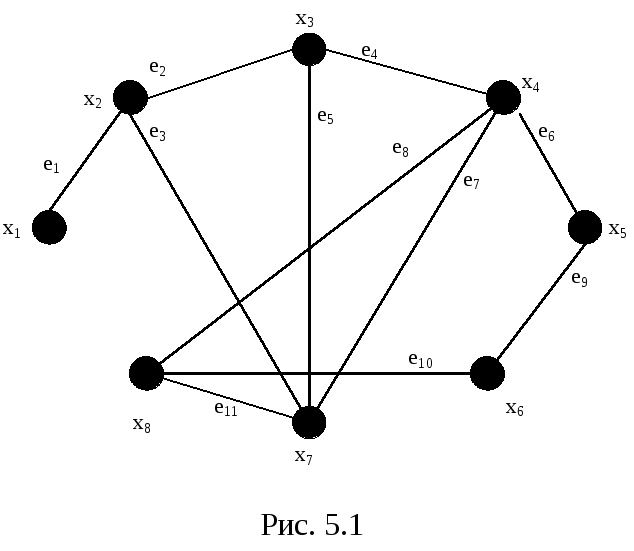ример 5.1.В неориентированном графеG, приведенном на рис. 5.1 цепь₁ = {e₁, e₂, e₄, e₈, e₁₀}длиной 5 может быть задана как последовательностью ребер, так и последовательностью вершин₁ ={x₁, x₂, x₃, x₄, x₈, x₆}. В этой цепи вершинаx₁является начальной, а вершинаx₆— конечной. Последовательность ребер(e₂, e₄, e₈)— подцепь, выделенная из цепи₁. Цепь₂ = {e₁, e₂, e₄, e₇, e₅, e₄, e₇,e₃, . . .}является односторонне бесконечной.

Цепь ₃ = {e₄, e₈, e₁₀,e₉, e₆,e₇}является простой цепью, а₄ = {e₂, e₄, e₈, e₁₀}— элементарной. Циклом является замкнутая цепь₅ ={e₂, e₅, e₇, e₈, e₁₁, e₃}, а последовательность₆ = {e₂, e₄, e₈, e₁₁, e₃}образует элементарный цикл.

Теорема 5.1.ПустьG = (X,E)- неориентированный граф,A(G)– матрица смежности его вершин. Тогда элементc_ijматрицы C = Aⁿ(G)равен числу различных цепей длиныn, соединяющих вершиныx_i иx_j.

Доказательство. Еслиa_ik– число ребер, соединяющих вершиныx_iиx_k,a_kj– число ребер, соединяющих вершиныx_kиx_j, то произведениеa_ik a_kj есть число различных маршрутов длины 2, соединяющих вершиныx_iиx_jи проходящих через вершинуx_k. Тогда

,

где p– число вершин графаG, есть число всех маршрутов длины 2, соединяющих вершиныx_iиx_j. С другой стороны,с_ijесть элемент матрицыA²(G), поэтому дляn= 2 теорема доказана.

Воспользуемся индукцией по nи предположим, что теорема верна дляm=n-1. Так какAⁿ(G) = A(G)A^n-1(G), то приведенные выше рассуждения доказывают справедливость теоремы дляm = n. Тем самым теорема доказана.

Следствие 5.1.В неориентированном графеGмаршрут длинойnсуществует тогда и только тогда, когдаAⁿ(G)  0.

Следствие 5.2.ЕслиAⁿ(G)=0для некоторогоn>0, то в неориен­ти­ро­ванном графе Gнет циклов.

Пусть G(X,E)— неориентированный граф. Две вершиныx_iиx_jназываются связными, если существует маршрутиз вершины x_iв вершинуx_j. Если маршрутпроходит через вершинуx_kболее одного раза, то можно, очевидно, удалить его циклический участок, и при этом оставшиеся ребра образуют маршрут, связывающийx_iиx_j. Отсюда следует, что связные вершины связаны элементарной цепью. Граф называется связным, если любая пара вершин связана, т.е. любые две вершины соединены цепью.

Пусть y -произвольная вершина неориентированного графаG = (X,E). Обо­значим черезX_yмножество всех вершин графаG, которые можно сое­динить сyцепями (вершинуyтакже включаем в множествоX_y). ПустьG_y— подграф графаG, множеством вершин которого является множествоX_y, а множество ребер образуют все те ребра изE, концы которых принадлежатX_y. Построенный таким образом подграфG_yназываетсякомпонентой связностиилисвязной компонентойграфаG.

Теорема 5.2.Компоненты связности неориентированного графаG обладают следующими свойствами.

1. G_y  0для любогоy  X.

2. Если G_y  G_z, тоG_y  G_z = .

3. .

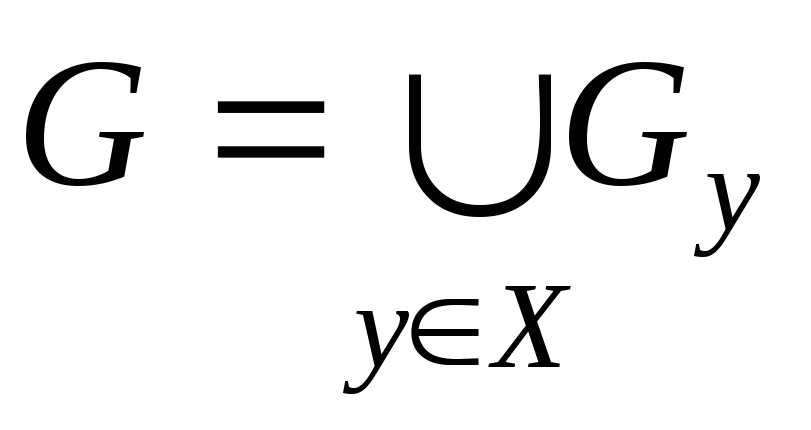Доказательство. Так как y  X_y, то первое свойство выполняется. Вто­рое свойство докажем от противного. ЕслиG_y  G_z  , тоX_y  X_z  . Тогда существует вершинаx  X_y  X_z, которую можно соединить цепями как сy, так и сz. Отсюда следует, что вершиныyиzможно соединить цепью, поэтомуX_y = X_z. В результате получаемG_y = G_z, что и доказывает второе свойство.

Третье свойство следует из определения компоненты связности графа.

Следствие 5.3.Неориентированный граф связен тогда и только тогда, когда он состоит из одной компоненты связности.

Условия, эквивалентные связности графа, сформулированы в следую­щем утверждении.

Теорема 5.3.Неориентированный графG = (X,E)связен тогда и только тогда, когда множество вершинXнельзя разбить на два непустых непересекающихся подмножестваX₁иX₂, которые не соединены ни одним ребром.

Доказательство.Необходимость указанного условия доказывается следующим образом. ЕслиX₁иX₂— указанное в теореме разбиение, то любая цепь, соединяющая вершиныx  X₁иy  X₂, должна содержать хотя бы одно ребро, соединяющее множестваX₁иX₂. Поскольку таких ребер нет, то вершиныxиyне могут быть соединены цепью. Это противоречит связности графаG, поэтому указанное разбиение не существует.

Доказательство достаточности следующее. Пусть Gне связен, и пустьG_y – его компонента связности со множеством вершинX_y. ТогдаX  X_y, множествоX₂ = X\X_yне пусто,X₂  X_y =. Ясно, чтоX₂иX_yне соединены ни одним ребром. Это противоречит условию теоремы, поэтому граф G связен. Теорема доказана.

Следствие 5.4.Неориентированный графGсвязен тогда и только тогда, когда не существует такой нумерации вершин графаG, при которой его матрица смежности вершин имеет вид

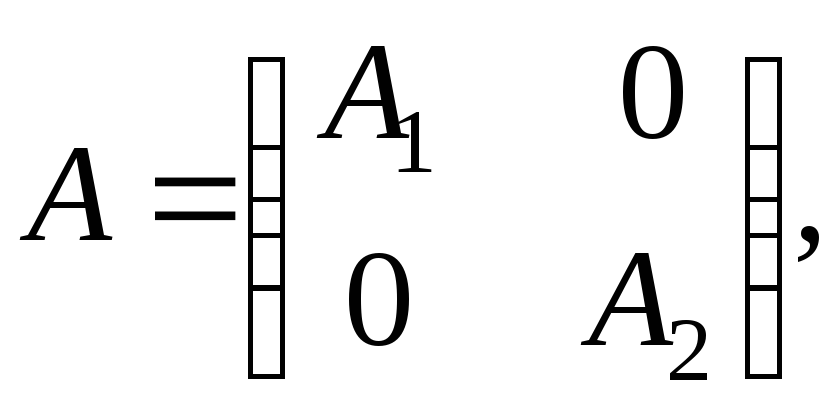
где A₁иA₂- квадратные матрицы.

Теорема 5.4.ПустьG – обыкновенный неориентированный граф сnвершинами иkкомпонентами связности. Тогда максимальное число ребер в графеGравно

.

Доказательство. Граф Gимеет максимальное число ребер, если каждая компонента связностиG_i, i = 1, 2, . . . , kимеет максимальное число ребер. Компонента связностиG_i, имеющая максимальное число ребер, является полным графом. Число ребер полного графа сn_iвершинами равно0,5n_i(n_i - 1). Таким образом, максимальное число ребер графаG, компоненты связностиG_iкоторого имеют поn_iвершин, равно

Полученное число зависит от того, как распределены вершины графа Gпо его компонентам связности. Предположим, что существует связные ком­понентыG₁иG₂графаG, имеющие более чем по одной вершине, т. е. n₁ > 1 иn₂ >1. Пустьn₁  n₂. Рассмотрим графG, получаемый из графаGзаменой компонентG₁иG₂на полные графы с(n₁-1)и(n₂+1)вершинами соответственно. ГрафGимеетnвершин иkкомпонент связности, а число его ребер равно

Тогда

поэтому q’ > q. Итак, графGимеет больше ребер, чем графG. Если и далее перестраивать граф указанным образом, то в результате получим граф, состоящий изk-1изолированной вершины и одной полной компоненты связности сn - k + 1вершиной. Этот граф имеет максимальное число ребер, равное0,5(n - k)(n - k + 1). Теорема доказана.

Следствие 5.5.Если обыкновенный неориентированный графGсnвершинами имеет больше, чем0,5(n - 1)(n - 2)ребер, то он связен.

Доказательство. Из теоремы 5.3 следует, что 0,5(n - 1)(n - 2)— максимальное число ребер в обыкновенном графе сnвершинами и двумя компонентами связности. Если же в графе больше, чем0,5(n - 1)(n - 2)ребер, то число компонент в нем либоk=1, либоk  3. Случайk  3 противоречит условию, поэтомуk = 1 и графGсвязен.

Ориентированный граф G(X,E)называетсясильно связным,если для любых его вершинxиy,xy, существуют путии, идущие соответственно изxвy и изyвx.

Рассмотрим теперь ориентированные графы. Пусть G(X,E,)– орграф. Конечная последовательность дугe₁, e₂, …, e_nграфаGназывается путем длинойn, или ориентированным маршрутом длиныn, если существует такая последовательность вершинx₀, x₁, …, x_n, что(e_i) = (x_i-1,x_i), гдеi= 1,2,…, . Путьзаписывается в виде ={e₁, e₂, …, e_n}или в виде = {x₀, x₁, …, x_n }. В этом случае говорят, что путь состоит из дугe₁, e₂, …, e_n, выходит из вершиныx₀и заходит в вершинуx_n. Путьназывается простым, если все его дуги различны, и элементарным, если все его вершины различны.

Пути и’ считаются равными, если они имеют одинаковую длину и состоят из одних и тех же дуг. В противном случае путии’ считаются различными.

Следующие утверждения доказываются точно так же, как это сделано для неориентированных графов в начале этого параграфа.

Теорема 5.5.ПустьG = (X,E)–орграф,A(G)– матрица смежности его вершин. Тогда элементc_ijматрицы C = Aⁿ(G)равен числу различных путей длинойn, выходящих из вершиныx_i и заходящих в вершинуx_j.

Следствие 5.6.В орграфеGпуть длинойnсуществует тогда и только тогда, когдаAⁿ(G)  0.

Следствие 5.7.ЕслиAⁿ(G)=0для некоторогоn>0, то в орграфе Gнет циклов.

Орграф G(X,E)называется сильно связным, если для любых его вершинxиy, xy, существуют пути и’, идущие соответственно изxвyи изyвx.

Т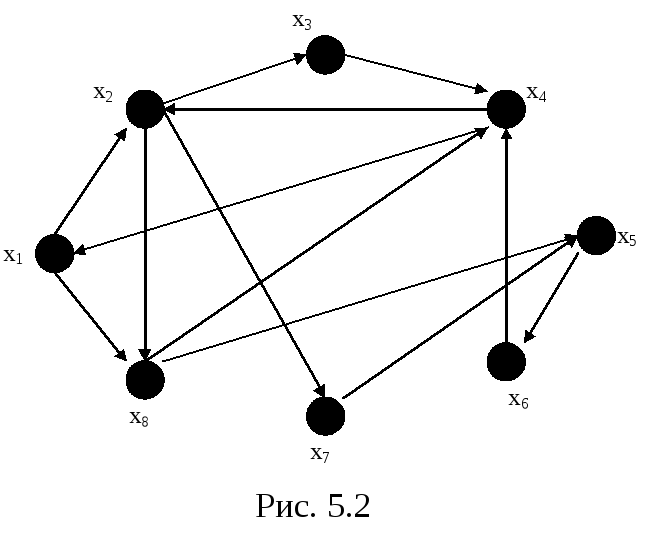еорема 5.6.ОрграфG(X,E)сильно связен тогда и только тогда, когда он имеет контур, проходящий через все вершины.

Доказательство. Пусть xиy– две вершины графаG, причемx  y. По условию теоремы существует путь₁, идущий из вершиныxв вершинуy.

Пусть X₁– множество вершин пути₁. ЕслиX₁ = X, то достаточно взять путь, идущий изxвyи получим контур₁  , проходящий через все вершины графа. Если жеX₁  X, тоX\X₁  . Тогда для вершиныz  X\X₁строим путь, идущий изyвz, и получаем путь₂ = ₁ .ПустьX₂– множество вершин пути₂. ТогдаX₂  X₁, X₂  X₁. Если продолжить этот процесс, то через конечное число шагов будет построен путь, содержащий все вершины графа, и, следовательно, искомый контур существует.

Пример сильно связного графа приведен на рис. 5.2.