Доказательство:

Пусть К-я симплекс-разность матрицы , (3.54)

и все (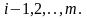3.55) Матрица определяет опорный план Рассмотрим вектор , у которого

где - любое положительное число. Остальные компонент вектора положим равными нулю. В силу условия (3.55) компонент вектора неотрицательные. Легко убедиться в том, что компоненты вектора удовлетворяют и функциональным ограничениям задачи линейного программирования, т.е. вектор - план задачи линейного программирования при любом положительном . Имеем:

или окончательно (3.56) Так как , то из (3.56) следует, что для любого числа всегда можно найти план ЗЛП, для которого т.е. линейная форма не ограничена сверху на множестве планов.

Теорема доказана.

9. Двухэтапный симплекс-метод. Ответ проиллюстрировать на примере:

Min f ( x ) = 4х₁+ 3х₂ + 2x₃

-х₁ - 2х₂ - x₃  -2

2х₁ + х₂ + x₃  10

х₁  0, х₂  0

Ответ:

min f ( x ) = 4х₁+ 3х₂ + 2x₃’-2x₃’’+0 x₄+0 x₅+0 x₆+0 x₇+0 x₈+0 x₉

-х₁ - 2х₂ - x₃’+ x₃’’ + x₄ = -2

2х₁ + х₂ + x₃’- x₃’’+ x₅ = 10

х₁ – x₆ = 0,

х₂ – x₇ = 0,

x₃’– x₈ =0,

x₃’’– x₉ =0

10. . М-метод решения ЗЛП. Решить М-методом ЗЛП:

Min f ( x ) = 4х₁+ 3х₂ + 2x₃ +Mu1 +Mu2 +Mu3+Mu4

х₁ + 2х₂ + x₃  2 -x4 +u1

2х₁ + х₂ + 2x₃  10 +x5

х₁  0 –x6 +u2, х₂  0 –x7 +u3 , x3>=0–x8 +u4

Ответ:

11. Модифицированный симплекс-метод: первый алгоритм.

Ответ проиллюстрировать на примере:

2. 3x₁+2x₂+3x₃  max

3. 2x₁+x₂+x₃ 20

4. 3x₁+4x₂+2x₃ 80

5. x₁ ,x₂ , x₃  0

На новой итерации Xns k-е = Bs(-1)*Xns;

12. Модифицированный симплекс-метод: второй алгоритм.

Ответ проиллюстрировать на примере:

2. 3x₁+2x₂+3x₃  max

3. 2x₁+x₂+x₃ 20

4. 3x₁+4x₂+2x₃ 80

5. x₁ ,x₂ , x₃  0

13. Двойственные задачи линейного программирования. Теоремы двойственности : сформулировать все, доказать теорему 1 (f(x) ≤ g(y) ).

Решить графическим методом и в ПОИСКЕ РЕШЕНИЙ задачу линейного программирования. Сформулировать двойственную задачу и найти ее оптимальный план с помощью теорем двойственности. Проиллюстрировать выполнение теорем двойственности, если исходная задача имеет вид

Min f ( X ) = 4X₁+ 3X₂

X₁ + 2X₂  10

X₁ + 2X₂  2

2X₁ + X₂  10

X₁  0, X₂  0

Ответ:

Д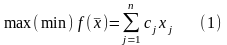 войственная задача- это вспомогательная задача линейного программирования, формулируемая с помощью определенных правил непосредственно из условий исходной или прямой задачи. В основу такого подхода положен тот факт, что использование симплекс- метод требует приведение любой ЗЛП к каноническому виду. Пусть прямая задача записана в каноническом виде:

З адачей, двойственной к ЗЛП, называется следующая ЗЛП:

Двойственная ЗЛП строится по следующим правилам: 1)Каждому ограничению прямой задачи соответствует переменная двойственной задачи,т.е. Число переменных двойственной задачи равно числу ограничений прямой задачи. 2)Каждой переменной прямой задачи соответствует ограничение двойственной задачи, т.е. Число ограничений двойственной задачи равно числу переменных прямой задачи. 3)Матрица функциональных ограничений двойственной задачи получается путём транспонирования матрицы функциональных ограничений прямой задачи. 4)Если целевая функция прямой задачи максимизируется,то целевая функция двойственной задачи минимизируется, а ограничения имеют вид больше либо равно, и наоборот.

Т еорема 1: Пусть , - планы соответственно прямой и двойственной ЗЛП, тогда

Д оказательство: Умножим неравенство (2) на Умножим неравенство (5) на Откуда следовательно теорема доказана.

Теорема 2 Пусть и - планы соответственно прямой и двойственной ЗЛП и , тогда и - решения соответственно прямой и двойственной задач (равенство целевых функций является достаточным условием оптимальности планов обеих задач).

Теорема 3 Если прямая (двойственная) ЗЛП имеет конечное решение, то и двойственная (прямая) ЗЛП имеет решение, причем Если прямая ЗЛП (двойственная) не имеет решения, то и двойственная ЗЛП не разрешима.

Теорема 4 Планы и соответственно прямой и двойственной ЗЛП являются оптимальными тогда и только тогда, когда , эти условия называются условиями дополнительной нежесткости.

Теорема 5 Для существования решения одной из пары двойственных задач (и, следовательно, обеих) необходимо и достаточно непустоты множества планов P и Q.

Теорема 6 Планы и оптимальны тогда и только тогда, когда

Теорема 7 Если функция не ограничена сверху ( - снизу) на множестве P(Q), то Q=ø (P=ø).

Теорема 8 Если P=ø (Q=ø) ,а Q!=Ø (P!=Ø), то Q – неограниченное множество и g(y) не ограничена снизу на нем (P - не ограниченное множество и не ограничена сверху на нем).

14. Теоремы двойственности : сформулировать все, доказать теорему 2(достаточное условие оптимальности).

Ответ:

Теорема 2 Пусть и - планы соответственно прямой и двойственной ЗЛП и , тогда и - решения соответственно прямой и двойственной задач (равенство целевых функций является достаточным условием оптимальности планов обеих задач).

Доказательство: Пусть , тогда в силу предыдущей теоремы для пары можно записать: Следовательно Т.е. есть решение ИЗ. Пусть , тогда в силу предыдущей теоремы для пары : Следовательно то есть решение ДЗ.

15. Двойственные задачи линейного программирования. Теоремы двойственности : сформулировать все, доказать теорему 5 (необходимое и достаточное условие оптимальности – непустота множества планов)

Ответ: Необходимость: ИЗ разрешима, следовательно план P – не пустое множество ДЗ разрешима план Q - не пустое множество. Достаточность: дано ø и ø, 1) - произвольная точка - фиксированная точка Из 2-ой теоремы двойственности: Ц.ф. ограничена сверху на ø по т.Вейерштрассе ЗЛП разрешима.

16. Экономическая интерпретация двойственных переменных (на примере задачи распределения ресурсов):

Для изготовления трех видов продукции используют три вида сырья. Запасы сырья, нормы его расхода и цена каждого продукта приведены в таблице.

Тип	Нормы расхода сырья на одно изделие			Запасы
Сырья	А	Б	В	сырья
I	4	2	1	180
II	3	1	3	210
III	1	2	5	244
Цена	10	14	12

При решении задачи на максимум общей стоимости выпускаемой продукции были получены следующие результаты:

Х1 = 0, Х2 =82, Х3 = 16.

Требуется:

1) Сформулировать прямую оптимизационную задачу на максимум общей стоимости, сформулировать двойственную задачу, найти оптимальный план двойственной задач, используя теоремы двойственности;

2) Определить, как изменится общая стоимость продукции и план выпуска при увеличении запасов сырья I и III вида на 4 ед. каждого;

3) Определить целесообразность включения в план изделия "Г", на изготовление которого расходуется соответственно 1, 3 и 2 ед. каждого вида сырья ценой 13 ед. и изделия "Д" на изготовление которого расходуется по две единицы каждого вида сырья ценой 12 ед.

17, Получение решения двойственной задачи из симплекс-таблицы решения прямой задачи (с доказательством). Проиллюстрировать метод на примере задачи распределения ресурсов:

Max f ( x ) = 2х₁+ 3 х₂

х₁ + х₂  200

2 х₁ + х₂  400

х₁  0, х₂  0

Ответ: Пусть прямая задача имеет вид основной ЗЛП. (1) Двойственная к ней ЗЛП имеет вид (2) Предположим , что ЗЛП (1) имеет решение. Для его получения приведём основную ЗЛП (1) к каноническому виду. (3)

Расширенная матрица системы линейных уравнений (3) является К-матрицей ,следовательно, ЗЛП (3) можно решить симплекс-методом. Матрицу К⁽⁰⁾ запишем в виде где a_j- j-ый столбец матрицы А, e_j- единичный столбец. Предположим, что на S-ой итерации симплекс – метода получен оптимальный опорный план X*, определяемый К- матрицей И вектором . Векторы образуют базисную (единичную) подматрицу в матрице , следовательно, векторы исходной матрицы образуют базисную подматрицу в матрице . Следовательно можно записать: Где -матрица , обратная для базисной подматрицы . Матрица расположена на месте единичной подматрицы (единичных столбцов) исходной матрицы . Так как на S-ой итерации получен оптимальный опорный план То отвечающие матрице симплекс-разности являются неотрицательными (125) Или (4) Обозначим И покажем, что вектор У* является решением двойственной ЗЛП .Действительно, рассматривая первые n неравенств (125) и записывая их в матричной форме, имеем Аналогично, рассматривая неравенства (4) для j=n+1,…,n+m и учитывая, что получаем (7) или (8). Из соотношений (6) и (8) следует, что У*-план двойственной ЗЛП (2). Далее Следовательно. По второй теореме У*- решение двойственной ЗЛП (2). Из выражения (7) (9) Следует, что I- компонента Y^*_I -решение двойственной ЗЛП есть (n+i)-я симплекс-разность матрицы , определяющей оптимальный план исходной ЗЛП. Из выражения (4) следует, что j-я симплекс-разность матрицы равна разности между левой и правой частью ограничений двойственной ЗЛП:

18. Метод ветвей и границ (МВГ). Применение МВГ к решению целочисленной ЗЛП (ЦЗЛП). Проиллюстрировать метод на примере ЦЗЛП:

Max f ( x ) = х₁+ 1.3 х₂

8х₁ + 6х₂  61

х₁ + 2 х₂  12

х₁  0, х₂  0, х₁, х₂ – целые.

19. Транспортная задача (ТЗ): постановка задачи, модель, закрытая и открытая модели ТЗ. Методы получения первоначального опорного плана ТЗ. Обоснование критерия оптимальности ТЗ. Проиллюстрировать метод на примере ТЗ:

6	-	4	-	500
8	8	2	6	300
9	-	7	6	100
400	200	150	250	ai bj

Ответ:

Постановка задачи: Некоторый однородный продукт, сосредоточенный у m поставщиков А_i в количестве а_i(i = 1, ..., m) единиц соответственно, необходимо доставить n потребителям В_j в количестве b_j(j = 1,..., n) единиц. Известна стоимость с_ij перевозки единицы груза от i-го поставщика к j-му потребителю. Необходимо составить план перевозок, позволяющий вывести все грузы, полностью удовлетворить потребности и имеющий минимальную стоимость. Обозначим через х_ij количество единиц груза, запланированных к перевозке от i-го поставщика к j-му потребителю. Так как от i-го поставщика к j-му потребителю запланировано к перевозке х_ij единиц груза, то стоимость перевозки составит с_ijx_ij. Стоимость всего плана выразится двойной суммой: . Систему ограничений получаем из следующих условий задачи: а) все грузы должны быть перевезены, т.е. б) все потребности должны быть удовлетворены, т.е. . Таким образом, математическая модель транспортной задачи имеет следующий вид: найти минимальное значение линейной функции ;(6.1) при ограничениях ; (6.2) (6.3) x_ij  0, i = 1,…,m; j = 1,…, n. (6.4) В рассмотренной модели предполагается, что суммарные запасы равны суммарным потребностям, т.е. . (6.5) Транспортная задача, в которой суммарные запасы и потребности совпадают, т.е. выполняется условие (6.5), называется закрытой моделью; в противном случае – открытой. Для открытой модели может быть два случая: а) суммарные запасы превышают суммарные потребности ; б) суммарные потребности превышают суммарные запасы . Линейная функция одинакова в обоих случаях, изменяется только вид системы ограничений. Найти минимальное значение линейной функции: . При ограничениях (случай «а») (случай «б») Открытая модель решается приведением к закрытой модели. В случае «а», когда суммарные запасы превышают суммарные потребности, вводится фиктивный потребитель В_{n + 1}, потребность которого: . В случае «б», когда суммарные потребности превышают суммарные запасы, вводится фиктивный поставщик А_{m + 1}, запасы которого: . Как стоимость перевозки единицы груза до фиктивного потребителя, так и стоимость перевозки груза от фиктивного поставщика полагаются равными нулю, поскольку груз в обоих случаях не перевозится. Транспортная задача имеет n + m уравнений с mn неизвестными. Матрицу Х = (х_ij)_m,n, удовлетворяющую условиям (6.2) - (6.4), называют планом перевозок транспортной задачи (х_ij-перевозками). План Х*, при котором целевая функция (6.1) обращается в минимум, называется оптимальным. План транспортной задачи называется опорным, если из его основных коммуникаций невозможно составить замкнутый маршрут.

Методы получения первоначального опорного плана.

Метод северо-западного угла.

Используется для нахождения произвольного опорного плана транспортной задачи.

Метод минимального элемента.

П озволяет построить начальный опорный план транспортной задачи и является вариантом метода северо-западного угла, учитывающим специфику матрицы . В отличие от метода северо-западного угла данный метод позволяет сразу получить достаточно экономичный план и сокращает общее количество итераций по его оптимизации.

Решение задачи.

Методом северо-западного угла.