
- •4. Основные теоремы линейного программирования: сформулировать все, доказать теорему о существовании опорного плана (теорема 3).
- •5. Основные теоремы линейного программирования: сформулировать все, доказать теорему об оптимальности выпуклой комбинации планов злп (теорема 4).
- •6. Основные теоремы линейного программирования: сформулировать все, доказать теорему о существовании оптимального опорного плана злп (теорема 5).
- •Доказательство:
- •20. Обоснование решения транспортной задачи (тз) методом потенциалов. Проиллюстрировать метод на примере тз:
- •22. Постановка задачи динамического программирования (дп). Рекуррентные уравнения Беллмана (обратное и прямое), метод Беллмана. Решить методом Беллмана задачу распределения инвестиций:
- •23. Постановка задачи динамического программирования (дп). Рекуррентные уравнения Беллмана (обратное и прямое), метод Беллмана. Решить методом Беллмана задачу замены оборудования:
- •24. Управление запасами: стационарный детерминированный спрос. Формулы Уилсона.
- •28. Постановка задачи динамического программирования (дп). Рекуррентные уравнения Беллмана (обратное и прямое), метод Беллмана. Решить методом Беллмана задачу:
- •29. Определение оптимальных уровней запасов y* при вероятностном спросе и линейных функциях затрат.
ВОПРОСЫ по ИОиМО – июнь 11 г.
1. Постановка ЗЛП. Общая, основная, каноническая ЗЛП. Приведение общей ЗЛП к канонической форме. План, опорный план ЗЛП.
Привести к КЗЛП:
Max f ( x ) = 3X1 + 2X2
X1 + 2X2 ≤ 11
2X1 - X2 ≥ 5
X1 + 3X2 = 14
X2 ≥ 0
Ответ:
Постановка задачи: найти значения переменных Х1, Х2, Е, Хn , максимизирующие линейную форму: f (х1, х2, ..., хn ) = с1х1 + ... +сnхn ,(0.1)
при условиях :

 (0.2)
(0.2)
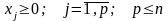 (0.3)
(0.3)
Соотношения (0.2) и (0.3)
будем называть соответственно
функциональными и прямыми ограничениями
ЗЛП. План
 будем
называть решением задачи линейного
программирования или ее оптимальным
планом, если
будем
называть решением задачи линейного
программирования или ее оптимальным
планом, если
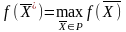
Основная ЗЛП является частным случаем общей ЗЛП при m1 = m, p = n.
В канонической форме
все функциональные ограничения записываются в виде равенств с неотрицательной правой частью;
все переменные неотрицательны;
целевая функция подлежит максимизации.
Любую ЗЛП можно привести к каноническому виду, используя следующие правила:
а) максимизация целевой функции
f(x) = C1X1 + C2X2 + ... + CnXn
равносильна минимизации целевой функции
f(x) = - C1X1 - C2X2 - ... - CnXn;
б) ограничение в виде неравенства, например
3Х1 + 2Х2 - Х3 <= 6, может быть приведено к стандартной форме
3Х1 + 2Х2 - Х3 + Х4 = 6, где новая переменная Х4 неотрицательна.
в) если некоторая переменная ХК может принимать любые значения, а
требуется, чтобы она была неотрицательная, ее можно привести к виду
 где
где
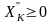 и
и
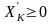 .
.
Планом или допустимым
решением задачи линейного программирования
будем называть вектор пространства
Еn, компоненты которого
удовлетворяют функциональным и прямым
ограничениям задачи. Опорным планом (
ОП ) задачи линейного программирования
будем называть такой ее план, который
является базисным решением системы
линейных уравнений
![]()
КЗЛП:
Max f ( x ) = 3X1 + 2X2+ 0X3+ 0X4
X1 + 2X2 + X3= 11
2X1 - X2 – X4 = 5
X1 + 3X2 = 14
X2 ≥ 0
2. Графический метод решения ЗЛП.
Решить задачу графическим методом и провести анализ на чувствительность, ответив на вопросы 1-5.
Для приготовления двух видов продукции (A, B) используют три вида сырья. Ресурсы сырья, норма его расхода на единицу продукции и цена продукции заданы в соответствующей таблице.
Определить план выпуска продукции из условия максимизации его стоимости.
Определить интервал изменения цены на продукцию А, при котором структура оптимального решения останется неизменной.
Определить интервал изменения цены на продукцию В, при котором структура оптимального решения останется неизменной.
Определите статус, ценность каждого ресурса и его приоритет при решении задачи увеличения запаса ресурсов.
Определите максимальный интервал изменения запасов каждого из ресурсов, в пределах которого структура оптимального решения, то есть номенклатура выпускаемой продукции, остается без изменения.
Сырье |
Норма расходов |
Ресурсы
|
|
A |
B |
|
|
I |
2 |
1 |
2700 |
II |
1 |
8 |
3200 |
III |
5 |
- |
1500 |
Ответ:
Графическим методом целесообразно решать ЗЛП, содержащие не более двух переменных.
Сырье |
Норма расходов |
Ресурсы |
|
A |
B |
|
|
I |
2 |
1 |
2700 |
II |
1 |
8 |
3200 |
III |
5 |
- |
1500 |
|
11 |
3 |
|
1) f(x)=11x1+3x2
2 |
1 |
<= |
2700 |
1 |
8 |
<= |
3200 |
5 |
0 |
<= |
1500 |
x1= |
300 |
|
|
x2= |
362,5 |
f(x)= |
4387,5 |
2) угол наклона линии уровня должен быть между углами наклона ограничений образующих вершину оптимального плана
3. Основные теоремы линейного программирования: сформулировать все, доказать теорему о крайней точке (Т 1).
Ответ:
Теорема 1 (о крайней точке)
Опорный план КЗЛП является крайней точкой множества P и наоборот.
Доказательство:
Пусть вектор
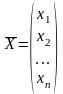 - опорный план ЗЛП, у которого компоненты
- опорный план ЗЛП, у которого компоненты
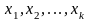 строго
положительные, а остальные (n-k)
компонент равны нулю. Тогда согласно
определению (2) опорного плана векторы
строго
положительные, а остальные (n-k)
компонент равны нулю. Тогда согласно
определению (2) опорного плана векторы
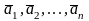 линейно независимы.
линейно независимы.
Предположим, что
вектор
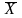 не является крайней точкой множества
, т.е. существуют векторы
не является крайней точкой множества
, т.е. существуют векторы

 и
и
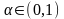 такие
что
такие
что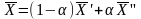 (1.1)
Векторы
(1.1)
Векторы
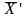 и
и
 -планы ЗЛП. Это означает, во-первых, что
компоненты векторов
-планы ЗЛП. Это означает, во-первых, что
компоненты векторов
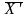 и
неотрицательные и вследствие (1.1) ровно
k компонент данных векторов
могут быть строго положительными.
Остальные (n-k)
компонент каждого из этих векторов
равны нулю. Во-вторых, компоненты векторов
и
удовлетворяют функциональным ограничениям
и
неотрицательные и вследствие (1.1) ровно
k компонент данных векторов
могут быть строго положительными.
Остальные (n-k)
компонент каждого из этих векторов
равны нулю. Во-вторых, компоненты векторов
и
удовлетворяют функциональным ограничениям
 ЗЛП. Следовательно
ЗЛП. Следовательно
 Вычитая из первого равенства
второе получим
Вычитая из первого равенства
второе получим
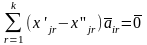 (1.2)
так как векторы
(1.2)
так как векторы
 линейно независимы, то из (1.2) следует
что
линейно независимы, то из (1.2) следует
что
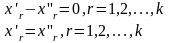 Следовательно
Следовательно
 Получено противоречие, следовательно
-крайняя
точка множества
Получено противоречие, следовательно
-крайняя
точка множества
 .
.
Обратно. Пусть теперь
вектор
- крайняя точка множества
,
строго положительными компонентами
которой являются
 Т к вектор
-
план ЗЛП, то его компоненты удовлетворяют
функциональным ограничениям
Задачи, т. е. имеет место равенство
Т к вектор
-
план ЗЛП, то его компоненты удовлетворяют
функциональным ограничениям
Задачи, т. е. имеет место равенство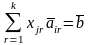 (1.3)
Предположим что вектор
не является опорным планом ЗЛП тогда
согласно определению (2) опорного плана
векторы
(1.3)
Предположим что вектор
не является опорным планом ЗЛП тогда
согласно определению (2) опорного плана
векторы линейно зависимы, т.е. существуют такие
действительные числа
линейно зависимы, т.е. существуют такие
действительные числа
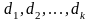 ,
не все равные нулю, что
,
не все равные нулю, что
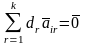 (1.4) Зададим некоторое
(1.4) Зададим некоторое
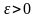 .
Умножим левую и правую части равенства
(1.4) сначала на
.
Умножим левую и правую части равенства
(1.4) сначала на
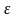 ,
затем на
,
затем на
 ,
Каждое из полученных равенств сложим
с (1.3), в результате получим
,
Каждое из полученных равенств сложим
с (1.3), в результате получим
 (1.5)
(1.5)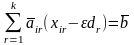 (1.6)
Выберем ε настолько малым, чтобы
выполнялись неравенства
(1.6)
Выберем ε настолько малым, чтобы
выполнялись неравенства
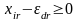 (1.7)
(1.7)
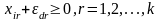 (1.8)
Рассмотрим векторы
и
(1.8)
Рассмотрим векторы
и
 ,
у каждого из которых отличными от 0 могут
быть лишь k компонент
,
у каждого из которых отличными от 0 могут
быть лишь k компонент
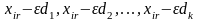 и
и
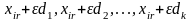 соответственно, а остальные (n-k)
компонент равны нулю. Согласно (1.5)-(1.8)
векторы
и
являются планами ЗЛП. Имеем
соответственно, а остальные (n-k)
компонент равны нулю. Согласно (1.5)-(1.8)
векторы
и
являются планами ЗЛП. Имеем
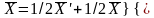 Т.е. вектор
лежит внутри отрезка, соединяющего две
различные точки
и
множества
Т.е. вектор
лежит внутри отрезка, соединяющего две
различные точки
и
множества
Последнее означает, что - не крайняя точка множества . Получилось противоречие, следовательно, - опорный план ЗЛП
Теорема 2(о сущесвованиии оптимального плана или решения задачи ЗЛП)
Если линейная форма
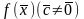 ограничена сверху на непустом множестве
,
то ЗЛП разрешима, т.е. существует такая
точка
ограничена сверху на непустом множестве
,
то ЗЛП разрешима, т.е. существует такая
точка
 ,
что
,
что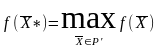
Теорема 3
Если множество не пусто, то оно имеет опорный план (или крайнюю точку)
Теорема 4
Пусть векторы
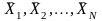 планы задачи линейного программирования.
Тогда вектор
планы задачи линейного программирования.
Тогда вектор
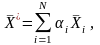 (4.1) где
(4.1) где
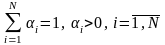 (4.2)
будет решением задачи ЗЛП тогда и только
тогда, когда её решением является каждый
из векторов
(4.2)
будет решением задачи ЗЛП тогда и только
тогда, когда её решением является каждый
из векторов
Теорема 5
Пусть вектор
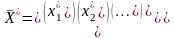 является решением ЗЛП. Тогда во множестве
планов
является решением ЗЛП. Тогда во множестве
планов
 существует крайняя точка, в которой
линейная форма
существует крайняя точка, в которой
линейная форма
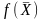 достигает
своего глобального максимума в области
достигает
своего глобального максимума в области
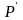 .
.
Теорема 6
Если решение ЗЛП достигается в нескольких крайних точках области , то оно достигается и в любой выпуклой линейной комбинации этих точек.
Утверждение теоремы 6 является следствием теоремы 4.
4. Основные теоремы линейного программирования: сформулировать все, доказать теорему о существовании опорного плана (теорема 3).
Ответ:
Теорема 1 (о крайней точке)
Опорный план КЗЛП является крайней точкой множества P и наоборот.
Теорема 2(о сущесвованиии оптимального плана или решения задачи ЗЛП)
Если линейная форма ограничена сверху на непустом множестве , то ЗЛП разрешима, т.е. существует такая точка , что
Теорема 3
Если множество не пусто, то оно имеет опорный план (или крайнюю точку)
Доказательство:
Заметим что если правые части
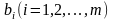 системы линейных уравнений равны нулю,
то, т.к. ранг матрицы A
равен m, вектор
системы линейных уравнений равны нулю,
то, т.к. ранг матрицы A
равен m, вектор
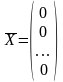 является вырожденным опорным планом
ЗЛП. Поэтому далее будем предполагать
, что среди
является вырожденным опорным планом
ЗЛП. Поэтому далее будем предполагать
, что среди
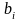 есть отличные от нуля.
есть отличные от нуля.
Пусть вектор
- план, но не опорный
план ЗЛП с k строго
положительными компонентами. Не нарушая
общности, будем считать, что строго
положительными являются первые k
компонент вектора
,
тогда имеет место равенство (3.1)
Так как вектор
(3.1)
Так как вектор
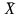 - не опорный план, то согласно определению
(2) опорного плана
- не опорный план, то согласно определению
(2) опорного плана
 Линейно зависимы, т.е. существуют
действительные числа
Линейно зависимы, т.е. существуют
действительные числа
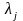 не все равные нулю и такие, что
не все равные нулю и такие, что (3.2)
(3.2)
Введём обозначение
 (3.3) Изменением знака в (3.2) можно всегда
добиться, чтобы
(3.3) Изменением знака в (3.2) можно всегда
добиться, чтобы
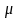 было положительным. Умножим левую и
правую части (3.2) на
было положительным. Умножим левую и
правую части (3.2) на
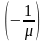 и полученное равенство сложим с (3.1),
будем иметь
и полученное равенство сложим с (3.1),
будем иметь
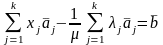 Или, так как
Или, так как
 ,
,
 (3.4) В силу (3.3)
(3.4) В силу (3.3) 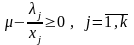 (3.5)
И обязательно существует такое j,
для которого с соотношении (3.5) имеет
место равенство. Положим для определённости
что
(3.5)
И обязательно существует такое j,
для которого с соотношении (3.5) имеет
место равенство. Положим для определённости
что
 Т.о., мы построили план ЗЛП, j-ая
компонента которого есть
Т.о., мы построили план ЗЛП, j-ая
компонента которого есть
 а остальные n-k+1
компонент равны нулю. При этом,если
векторы
а остальные n-k+1
компонент равны нулю. При этом,если
векторы
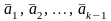 оказались линейно зависимыми, то,
рассуждая аналогично, получим план ЗЛП,
у которого k-2
строго положительных компонент > 0 и
т.д. до тех пор пока не построим такой
план ЗЛП с
оказались линейно зависимыми, то,
рассуждая аналогично, получим план ЗЛП,
у которого k-2
строго положительных компонент > 0 и
т.д. до тех пор пока не построим такой
план ЗЛП с
 строго положительными компонентами,
что соответствующие этим компонентам
векторы
строго положительными компонентами,
что соответствующие этим компонентам
векторы
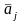 будут линейно независимыми. Так как по
предположению среди
будут линейно независимыми. Так как по
предположению среди
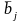 есть отличные от нуля, то
есть отличные от нуля, то
 .
Построенный план является при l=m
невырожденным, а при l<m
вырожденным опорным планом ЗЛП.
.
Построенный план является при l=m
невырожденным, а при l<m
вырожденным опорным планом ЗЛП.
Теорема доказана.
Теорема 4
Пусть векторы планы задачи линейного программирования. Тогда вектор
(4.1) где (4.2) будет решением задачи ЗЛП тогда и только тогда, когда её решением является каждый из векторов
Теорема 5
Пусть вектор является решением ЗЛП. Тогда во множестве планов существует крайняя точка, в которой линейная форма достигает своего глобального максимума в области .
Теорема 6
Если решение ЗЛП достигается в нескольких крайних точках области , то оно достигается и в любой выпуклой линейной комбинации этих точек.
Утверждение теоремы 6 является следствием теоремы 4.
5. Основные теоремы линейного программирования: сформулировать все, доказать теорему об оптимальности выпуклой комбинации планов злп (теорема 4).
Ответ:
Теорема 1 (о крайней точке)
Опорный план КЗЛП является крайней точкой множества P и наоборот.
Теорема 2(о сущесвованиии оптимального плана или решения задачи ЗЛП)
Если линейная форма ограничена сверху на непустом множестве , то ЗЛП разрешима, т.е. существует такая точка , что
Теорема 3
Если множество не пусто, то оно имеет опорный план (или крайнюю точку)
Теорема 4
Пусть векторы планы задачи линейного программирования. Тогда вектор
(4.1) где (4.2) будет решением задачи ЗЛП тогда и только тогда, когда её решением является каждый из векторов
Доказательство:
Пусть каждый из
векторов
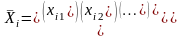 является решением ЗЛП, т.е.
является решением ЗЛП, т.е.
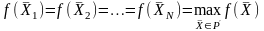 Тогда
Тогда

 т.е.
вектор
т.е.
вектор
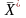 ,
определяемый соотношениями 4.1-4.2 также
является решением ЗЛП. Обратно, пусть
вектор
где
,
определяемый соотношениями 4.1-4.2 также
является решением ЗЛП. Обратно, пусть
вектор
где 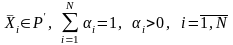 Является решением ЗЛП Предположим, что
среди векторов
есть хотя бы один вектор
Является решением ЗЛП Предположим, что
среди векторов
есть хотя бы один вектор
 ,
который не является решением ЗЛП, т.е.
имеет место следующее неравенство:
,
который не является решением ЗЛП, т.е.
имеет место следующее неравенство: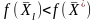 Тогда, учитывая 4.2, будем иметь
Тогда, учитывая 4.2, будем иметь
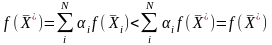 Получили противоречие, следовательно,
каждый из векторов
есть решение ЗЛП.
Получили противоречие, следовательно,
каждый из векторов
есть решение ЗЛП.
Теорема доказана
Теорема 5
Пусть вектор является решением ЗЛП. Тогда во множестве планов существует крайняя точка, в которой линейная форма достигает своего глобального максимума в области .
Теорема 6
Если решение ЗЛП достигается в нескольких крайних точках области , то оно достигается и в любой выпуклой линейной комбинации этих точек.
Утверждение теоремы 6 является следствием теоремы 4.

