6. Основные теоремы линейного программирования: сформулировать все, доказать теорему о существовании оптимального опорного плана злп (теорема 5).

Ответ:

Теорема 1 (о крайней точке)

Опорный план КЗЛП является крайней точкой множества P и наоборот.

Теорема 2(о сущесвованиии оптимального плана или решения задачи ЗЛП)

Если линейная форма ограничена сверху на непустом множестве , то ЗЛП разрешима, т.е. существует такая точка , что

Теорема 3

Если множество не пусто, то оно имеет опорный план (или крайнюю точку)

Теорема 4

Пусть векторы планы задачи линейного программирования. Тогда вектор

(4.1) где (4.2) будет решением задачи ЗЛП тогда и только тогда, когда её решением является каждый из векторов

Теорема 5

Пусть вектор является решением ЗЛП. Тогда во множестве планов существует крайняя точка, в которой линейная форма достигает своего глобального максимума в области .

Доказательство:

Заметим, что так как по условию теоремы множество не пусто, то согласно теореме 3 оно имеет хотя бы одну крайнюю точку. Рассмотрим два случая:

Случай 1: Пусть - выпуклый многогранник, а - решение ЗЛП. Тогда согласно теореме о представлении (Любая точка выпуклого замкнутого ограниченного множества К может быть представлена в виде линейной комбинации конечного числа крайних точек этого множества)

(5.1.1) где - крайние точки множества .

Выбросим из системы крайних точек те, которые входят в разложение (5.1.1) с коэффициентом Пусть это будут точки Тогда т.е. выполняется условие теоремы 4, и, следовательно, что и доказывает теорему.

Случай 2: Пусть - неограниченное множество, а - конечное решение ЗЛП. Тогда можно указать такое положительное число что (5.2.1) Введём в ЗЛП дополнительное функциональное ограничение (5.2.2) И рассмотрим новую задачу линейного программирования (5.2.3) при условиях (5.2.4)

(5.2.5) (5.2.6) Множество планов задачи (5.2.3)- (5.2.6) обозначим Множество - ограниченное, а так как компоненты вектора удовлетворяют условиям (5.2.4)-(5.2.6) и , то является решением задачи (5.2.3)-(5.2.6). Следовательно, согласно доказанному в случае 1, во множестве существуют крайние точки такие, что (5.2.7) Если хотя бы одна крайняя точка не принадлежит гиперплоскости (5.2.8) то она является крайней точкой множества и теорема доказана. Пусть все крайние точки принадлежат гиперплоскости (5.2.8), т.е. имеют место равенства

тогда из (5.2.7) имеем что противоречит условию (5.2.1) выбора Теорема доказана.

Теорема 6

Если решение ЗЛП достигается в нескольких крайних точках области , то оно достигается и в любой выпуклой линейной комбинации этих точек.

Утверждение теоремы 6 является следствием теоремы 4.

7. Обоснование симплекс-метода решения КЗЛП: К-матрицы, условия перехода от одной К-матрицы к другой, изменение целевой функции при переходе от одной К-матрицы к другой, критерий оптимальности опорного плана, критерий неразрешимости ЗЛП (критерий неразрешимости без доказательства)

Ответ:

К-матрицей КЗЛП будем называть расширенную матрицу системы линейных уравнений, равносильной системе , содержащую единичную подматрицу на месте первых n своих столбцов и все элементы (n+1)-го которой неотрицательны. Число К-матриц конечно и не превышает. Каждая К-матрица определяет ОП КЗЛП и наоборот.

Теорема 1: Пусть в к-м столбце К-матрицы - есть хотя бы один строго положительный элемент ( , ). Тогда с помощью одного шага метода Жордана-Гаусса можно построить новую К-матрицу - 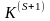, выбрав направляющий элемент из условия:

Условие перехода от одной К-матрицы к другой: Пусть в матрице есть и в столбце ( , ) есть хотя бы один строго положительный элемент. Тогда от матрицы можно перейти к матрице , причем

f ( ) f( ). (3.52)

_{Критерий оптимальности опорного плана: Пусть все симплекс-разности матрицы} неотрицательные. Тогда опорный план , определяемый матрицей , является оптимальным.

Доказательство:

По условию теоремы Или (3.52)

Пусть - произвольный план задачи линейного программирования. Умножим левую и правую части (3.52) на , тогда в силу неотрицательности получим (3.53) Согласно (3.53) имеем или , что и доказывает теорему.

Критерий неразрешимости ЗЛП: Пусть в матрице есть , и в столбце ( , ) нет ни одного строго положительного элемента. Тогда ЗЛП (3.18) не имеет конечного решения.

8. Обоснование симплекс-метода решения КЗЛП: К-матрицы, условия перехода от одной К-матрицы к другой, изменение целевой функции при переходе от одной К-матрицы к другой, критерий оптимальности опорного плана (критерий оптимальности без доказательства), критерий неразрешимости ЗЛП .

Ответ:

К-матрицей КЗЛП будем называть расширенную матрицу системы линейных уравнений, равносильной системе , содержащую единичную подматрицу на месте первых n своих столбцов и все элементы (n+1)-го которой неотрицательны. Число К-матриц конечно и не превышает. Каждая К-матрица определяет ОП КЗЛП и наоборот.

Теорема 1: Пусть в к-м столбце К-матрицы - есть хотя бы один строго положительный элемент ( , ). Тогда с помощью одного шага метода Жордана-Гаусса можно построить новую К-матрицу - , выбрав направляющий элемент из условия:

Условие перехода от одной К-матрицы к другой: Пусть в матрице есть и в столбце ( , ) есть хотя бы один строго положительный элемент. Тогда от матрицы можно перейти к матрице , причем

f ( ) f( ). (3.52)

_{Критерий оптимальности опорного плана: Пусть все симплекс-разности матрицы} неотрицательные. Тогда опорный план , определяемый матрицей , является оптимальным.

Критерий неразрешимости ЗЛП: Пусть в матрице есть , и в столбце ( , ) нет ни одного строго положительного элемента. Тогда ЗЛП (3.18) не имеет конечного решения.