39,40 Функции нескольких переменных
Функция 
переменных 
является
дифференцируемой в точке 
своей
области определения
,
если для любой точки 
существуют
такие константы 
,
что
где 
.
В этой записи функция
является
дифференциалом функции
в
точке
,
а числа 
являются частными
производными функции
в
точке
,
то есть
где 
—
вектор, все компоненты которого,
кроме 
-ой,
равны нулю, а
-ая
компонента равна 1.
Каждая
дифференцируемая в точке функция имеет
в этой точке все частные производные,
но не каждая функция, имеющая все частные
производные, является дифференцируемой.
Более того, существование частных
производных в некоторой точке не
гарантирует даже непрерывность функции
в этой точке. В качестве такого примера
можно рассмотреть функцию двух
переменных 
,
равную 
при 
и 
при 
.
В начале координат обе частные производные
существуют (равны нулю), но функция не
является непрерывной.
выше
выше
Частные производные первого порядка. Пусть функция
определена
в области 
и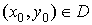 
.
Тогда при малых 
определено
ее частное приращение по 
: 
.
Определение. Частной
производной функции 
по
переменной
в
точке 
называют
предел
,
если он существует.
Частную производную по обозначают одним из следующих символов:
.
Аналогично
определяется частная производная по 
и
вводятся ее обозначения.
Легко видеть, что частная производная – это производная функции одной переменной, когда значение другой переменной фиксировано. Поэтому частные производные вычисляются по тем же правилам, что и вычисление производных функций одной переменной.
В математическом анализе, производная по направлению — это обобщение понятия производной на случай функции нескольких переменных. Производная по направлению показывает, насколько быстро функция изменяется при движении вдоль заданного направления.
Градие́нт (от лат. gradiens, род. падеж gradientis — шагающий, растущий) — вектор, своим направлением указывающий направление наискорейшего возрастания некоторой величины
,
значение которой меняется от одной
точки пространства к другой (скалярного
поля),
а по величине (модулю) равный быстроте
роста этой величины в этом направлении.Формула Тейлора показывает поведение функции в окрестности некоторой точки. Формула Тейлора функции часто используется при доказательстве теорем в дифференциальном исчислении.
Пусть функция
определена
на множестве 
и
точка 
.
Точка 
называется
точкой локального минимума (максимума)
функции
если 
.
Точки локального минимума (максимума)
называются точками локального экстремума.
Теорема (необходимое
условие экстремума). Пусть
функция
определена
в 
и
имеет локальный экстремум в точке
.
Если 
,
то 
.
Теорема (достаточное
условие локального экстремума). Пусть
функция
определена
в 
и
имеет в этой окрестности непрерывные
частные производные второго порядка.
Пусть 
.
Если 
является
знакоопределенной квадратичной формой,
тогда
-
точка локального экстремума, причем
если 
-
локальный минимум, а если 
-
локальный максимум.
Первообра́зной[1] или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.
Неопределённый интегра́л для функции
—
это совокупность всех первообразных данной
функции.
ТЕОРЕМА.
Пусть функция φ(t) имеет непрерывную
производную на отрезке [α,β], а=φ(α), в=φ(β)
и функция f(х) непрерывна в каждой точке
х вида х=φ(t), где t
[α,β].
Тогда справедливо следующее равенство:
Эта формула носит название формулы замены переменной в определенном интеграле.
Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы
для неопределённого интеграла:
для определённого:
Предполагается,
что нахождение интеграла 
проще,
чем 
.
В противном случае применение метода
неоправдано.