Устранимые точки разрыва

Если предел функции существует, но он не совпадает со значением функции в данной точке:

тогда точка   называется точкой устранимого разрыва функции   

Если «поправить» функцию   в точке устранимого разрыва и положить  , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением фукции до непрерывной или доопределением фукции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.

Точки разрыва первого и второго рода

Если предел функции в данной точке отсутствует (и функцию нельзя доопределить до непрерывной), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов:

7. теорема Вейерштрасса о максимальном значении. Функция, непрерывная на отрезке, ограничена на нем. При этом на отрезке есть точка, где функция принимает максимальное значение, и есть точка, где она принимает минимальное значение.

8. Равноме́рная непреры́вность в математическом и функциональном анализе — это свойство функции быть одинаково непрерывной во всех точках области определения.

9. Теоре́ма Ка́нтора — Ге́йне в математическом и функциональном анализе гласит, что функция, непрерывная на компакте, равномерно непрерывна на нём.

10. Дифференци́руемая (в точке) фу́нкция — это функция, у которой существует дифференциал (в данной точке). Дифференцируемая на некотором множестве функция — это функция, дифференцируемая в каждой точке данного множества. 

11. Дифференциа́л (от лат. differentia — разность, различие) — понятие математического анализа, линейная часть приращения функции.

12. f(x)=k=tg(x)

Производные простых функций

• 

• 

• 

•         когда   и 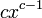  определены, 

Так как  , то пусть   и 

Тогда 

• 

• 

• 

• 

[

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

• 

 (частный случай формулы Лейбница)

 — Правило дифференцирования сложной функции

7. Цепное правило (правило дифференцирования сложной функции) позволяет вычислить производную композиции двух и более функций на основе индивидуальных производных. Если функция f имеет производную в точке  , а функция g имеет производную в точке  , то сложная функция h(x) = g(f(x)) также имеет производную в точке  .

[править]Одномерный случай

Пусть даны функции, определённые в окрестностях на числовой прямой,   где   и   Пусть также эти функции дифференцируемы:   Тогда их композиция также дифференцируема:   и её производная имеет вид:

[править]Замечание

В обозначениях Лейбница цепное правило для вычисления производной функции   где   принимает следующий вид:

[править]Инвариантность формы первого дифференциала

Дифференциал функции   в точке   имеет вид:

где   — дифференциал тождественного отображения  :

Пусть теперь   Тогда  , и согласно цепному правилу:

Таким образом, форма первого дифференциала остаётся одной и той же вне зависимости от того, является ли переменная функцией или нет.

[править]Пример

Пусть   Тогда функция   может быть записана в виде композиции   где

Дифференцируя эти функции отдельно:

получаем

[править]Многомерный случай

Пусть даны функции   где   и   Пусть также эти функции дифференцируемы:   и   Тогда их композиция тоже дифференцируема, и её дифференциал имеет вид

В частности, матрица Якоби функции   является произведением матриц Якоби функций   и 

[править]Следствия

Якобиан композиции двух функций является произведением якобианов индивидуальных функций:

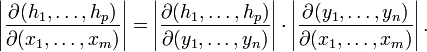
Для частных производных сложной функции справедливо

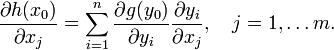
7. Для дифференцируемой функции с производной, отличной от нуля, производная обратной функции равна обратной величине производной данной функции, т.е

7. Лейбница формула

       формула, выражающая производную n-го порядка (см. Дифференциальное исчисление) от произведения двух функций через производные сомножителей:

        

        .

         Эта формула была сообщена Г. Лейбницем в письме к И. Бернулли в 1695. Л. ф. облегчает вычисление производных высших порядков.

7. Для любого натурального числа   уравнение

не имеет натуральных решений  ,   и  .

7. Если вещественная функция непрерывна на отрезке 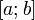  и дифференцируема на интервале  , принимает на концах этого интервала одинаковые значения, то на этом интервале найдётся хотя бы одна точка, в которой производная функции равна нулю.

 (Теорема Лагранжа) Пусть функция f(x)

1. непрерывна на отрезке [a, b];

2. дифференцируема в интервале (a, b).

Тогда существует точка с  (a, b) такая, что

 

f(b) − f(a) = f '(c) · (b − a) .

(Теорема Коши) Пусть функции f(x) и g(x)

1. непрерывны на отрезке [a, b];

2. дифференцируемы в интервале (a, b);

3. x  (a, b) g'(x) ≠ 0 .

Тогда существует точка c  (a, b) такая, что

 

f(b) − f(a) g(b) − g(a)    =   f '(c) g '(c)    .