Безопасность асинхронных вычислений

Сначала напомним, что как и сбоящие процессоры, так и планировщик имеют неограниченную вычислительную мощность.

Для вектора и множестваC[n]{1,...,n}, пусть определяет вектор, спроектированный на индексы изC. Для подмножестваB[n] и вектора , пустьопределяет вектор, полученный изподстановкой входов изBсоответствующими входами из. Используя эти определения, можно определить оценочную функциюfс базовым множествомC[n] как .

Пусть A– область возможных входов процессоров и пустьR– область случайных входов.ТР-противникэто кортежА=(B,h,c,O), гдеB[n] – множество сбоящих процессоров,h:A^BRA^B- функция подстановки входов,с:A^BR{C[n]Cn-t} – функция выбора базового множества иO:A^BRA{0,1}^*- функция выхода для сбоящих процессоров.

Функции hиOпредставляют собой программы сбоящих процессоров, а функцияc– комбинацию планировщика и программ сбоящих процессоров.

Пусть f:AⁿAдля некоторой областиA. Выход функции вычисленияfвТР-сценарии по входуи сТР-противникомА=(B,h,c,O) – этоn-размерный вектор =...случайных переменных, удовлетворяющих для каждого 1in:

=,

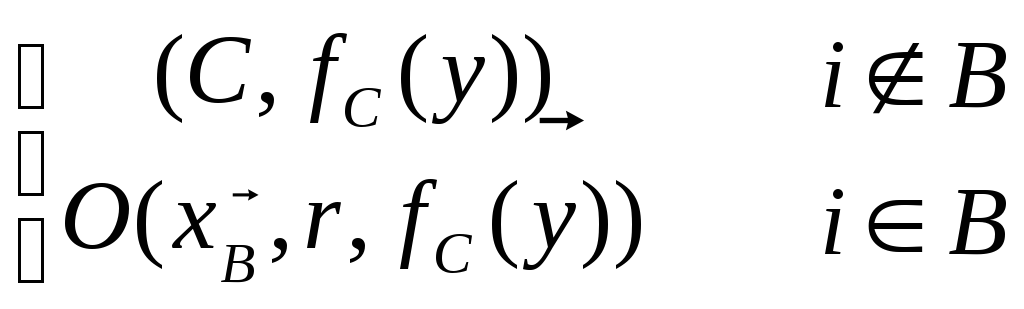где r- объединенный случайный вход сбоящих процессоров,C=и

Акцентируем внимание на то, что выход сбоящих процессоров и выход несбоящих процессоров вычисляется на одном и том же значении случайного входа r.

Далее формализуем понятие вычисления «в реальной жизни».

1. Пусть B=(B,) – коалиция нечестных процессоров, гдеB[n] – множество нечестных процессоров и- их совместная стратегия.

2. Пусть _i(,B,D) определяет выход процессораP_iпосле выполнения протокола_iпо входу , с планировщикомDи коалицииB. Пусть такжеP(,B,D)=₁(,B,D)..._n(,B,D).

Кроме того, пусть f:AⁿAдля некоторой областиA и пустьP- протокол дляnпроцессоров. Будем говорить, чтоPбезопасноt-вычисляет функциюfв асинхронной модели для каждой коалицииBс не более, чем изtсбоящих процессоров, если выполняются следующие условия.

Условие завершения (условие полноты).По всем входам все честные процессоры завершают протокол с вероятностью 1.

Условие безопасности. СуществуетТР-противникAтакой, что для каждого входавекторы(,A) иP(,B,D) идентично распределены (эквивалентны).

4. Конфиденциальное вычисление функции

Общие положения.Для некоторых задач, решаемых в рамках методологии конфиденциальных вычислений, достаточно введения определенияконфиденциального вычисления функции [MR].

Пусть в сети N, состоящей изnпроцессоровP₁,P₂,...,P_nсо своими секретными входамиx₁,x₂,...,x_n, необходимо корректно (даже при наличииtсбоящих процессоров) вычислить значение функции (y₁,y₂,...,y_n)=f(x₁,x₂,...,x_n) без разглашения информации о секретных аргументах функции, кроме той, информации, которая может содержаться в вычисленном значении функции.

По аналогии с идеальным и реальным сценариями, приведенными выше, можно ввести понятия «реальное и идеальное вычисление функции f» [MR].

Пусть множество входов и выходов обозначается как XиYсоответственно, размерности этих множествX=иY=. Множество случайных параметров, используемых всеми процессорами сети, обозначается черезR, размерность -R=. Кроме того, черезWобозначим рабочее пространство параметров сети. ЧерезT^(r)обозначается трафик вr-раунде, черезt_i^(r)– трафик для процессораiвr-том раунде,r₀иr_k– инициализирующий и последний раунды протоколаPсоответственно иr^*- заданный неким произвольным образом раунд выполнения протоколаP.

Пусть функцию fможно представить как композициюdфункций (суперпозицию функций)g₁...g_g_+1...g_d:

f(x₁,...,x_n)=

=g₁((w₁,...,w_n),(,...,))...g_((w₁,...,w_n),(,...,))...

g_d((w₁,...,w_n),(,...,)).

Аргументы функции g_являются рабочими параметрамиw₁,...,w_nучастников протокола с трафиком (t₁,...,t_n) вr раунде. Значения данной функцииg_являются аргументами (рабочими параметрами протокола с трафиком (t₁,...,t_n) вr+1 раунде) для функцииg_+1.

Из определения следует, что функция f:(XⁿRⁿW)Y, где- декартово произведение множеств, реализует:

f(x₁,...,x_n)=g_d((w₁,...,w_n),(,...,))=((y₁,...,y_n),(,...,)).

Введем понятие моделирующего устройства M. Здесь можно проследить некоторые аналогии с моделирующей машиной в интерактивных системах доказательств с нулевым разглашением (см., например, [Ка14,КУ4]).

Пусть _р^Прот- распределение вероятностей над множеством историй (трафикаТи случайных параметров) сбоящих процессоров во время выполнения протоколаР.

Моделирующее устройство, взаимодействующее со сбоящими процессорами, осуществляет свое функционирование в рамках идеального сценария. Моделирующее устройство Мсоздает распределение вероятностей параметров взаимодействия_и^ПротмеждуМи сбоящим процессорами.

Протокол Pконфиденциально вычисляет функциюf(x), если выполняются следующие условия:

Условие корректности.Для всех несбоящих процессоровP_iфункция

f(x₁,...,x_n)=

=g₁((w₁,...,w_n),(,...,))...g_((w₁,...,w_n),(,...,))

g_+1((w₁,...,w_n),(,...,))...g_d((w₁,...,w_n), (,...,))=

=((y₁,...,y_n),(,...,))

вычисляется с вероятностью ошибки близкой к 0.

Условие конфиденциальности.Для заданной тройки (x,r,w)(XⁿRⁿW) распределения_р^Проти_и^Протявляютсястатистически не различимыми.

Функция f, удовлетворяющая условиям предыдущего определения называетсяконфиденциально вычислимой.