24. Дифференциальные уравнения (основные понятия)

Ур-ние вида F (x,y,y’,y’’,…,y⁽ⁿ⁾)=0 назыв обыкновенным дифференц ур-нием n-порядка.Решением ДУ F (x,y,y’,y’’,…,y⁽ⁿ⁾)=0 наз ф-ция y=f(x) удовл ур-нию F (x,y,y’,y’’,…,y⁽ⁿ⁾)=0, т.е. такое для кот выполн тождество F (x,f(x), f’(x), … f⁽ⁿ⁾(x))=0График решения ДУ наз интегральной кривой.ДУ 1-го порядка наз ур-ние вида F (x,y,y’)=0. Продпол, что ур-ние можно решить относ производной y’= f(x,y).Общим уравнение ДУ y’= f(x,y) наз такая ф-ция y= f(x,с) кот при каждом зная с (из нек множеств явл решением ур-ния y’= f(x,y). Общ реш запис в неаявном виде F(x,y,c)=0 наз общим интегралом.Те решения которые получаются из общего решения путем фиксирования произвольной постоянной наз частными.

25. Дифференциальные уравнения первого порядка с разделяющимися переменными.

Наз ур-ния вида N(x)M(y)dx + P(x)Q(y) dy=0 где N(x),M(y), P(x),Q(y) ф-ции непрерывные на нек промежутке.Уравнение N(x)M(y)dx + P(x)Q(y) dy=0 разделим на произвед ф-ции P(x)*M(y). Получим N(x)dx/P(x) + Q(y) dy /M(y)=0. роинтегрируем получ уравнение и это есть общий интеграл ур-ния N(x)M(y)dx + P(x)Q(y) dy=0:

26Лин.дифф.ур-я 1-го порядка. таким ур-ем наз.ур-е вида: y’+p(x)y=f(x) (1),где p(x),f(x) непрерывны на некот.промежутке.Реш-е ур-я будем искать в виде:y’=vu’+uv’.Подставим y и y’ в ур-е (1):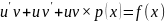 ; v’+vp(x)=0 ; ; –с разделяющим.переменными. (5)Интегрируемое ур-е(5): ; 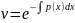(6).Подстановка в ур-е (4): ; 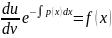.Разделим переменные: Интегрируем получ.ур-е: .Подставляем в ур-е(2): -общее реш-е ур-я.

27Диффер.ур-я 2-го порядка. Рассмотрим ДУ 2-го порядка: 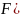Предположим, что можно выразить y’’: 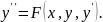Задача Коши: Дано: ДУ(1).Требуется найти решение, удовлет. условию: 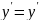0 0 0. X0 ,Y0, Y’0 –начальные данные.С теор.точки зрения это означает,что требуется найти интегр.кривую, проходящ. через т.М0( 0, 0) и имеющую в заданной точке угл.коэффициент Y0.

28) Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами. Линейными однородн. ДУ 2-го порядка с пост коэф наз ур-е вида: p,q – const Структура общ решения ур-ния: Теорема 1- Если у1 явл. решением ур-ния, то у=с*у₁ также явл. реш-нием уравнения. Теорема 2 – Если у₁ и у₂ реш. ур-ния, то у=у₁+у₂ также явл. реш-нием.Определение: Фун-ции у₁ и у₂ наз. линейно независимыми если их отношение не явл постоянной величиной. В противном случае ф-ции у₁ и у₂ наз. линейнозависимыми. Теорема 3: Если у₁ и у₂ это линейно независимые реш-ия уравнения , то ф-ция у=с₁*у₁+с₂*у₂ …с₁ и с₂ const , явл общим решением уравнения.

29) Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.Линейное неоднородное уравнение данного типа имеет вид: где p, q − постоянные числа (которые могут быть как действительными, так и комплексными). Для каждого такого уравнения можно записать соответствующее однородное уравнение: Теорема1: Общее решение неоднородного уравнения является суммой общего решения y0(x) соответствуюшего однородного уравнения и частного решения y1(x) неоднородного уравнения:

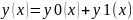
30) Понятие числового ряда и суммы ряда. Геометрическая прогрессия.Числовым рядом называется выражение вида: где u1,u2,…,u_n,… - действительные или комплексные числа, называемые членами ряда, u_n – общим членом ряда. Ряд считается заданным, если известен общий член ряда, выраженный как функция его номера n: u_n = f(n). Сумма первых n членов ряда называется n-ой частичной суммой ряда и обозначается через S_n. Если существует конечный предел S = последовательности частичных сумм ряда, то этот предел называют суммой ряда и говорят, что ряд сходится. Записывается: . Если не существует или 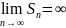, то ряд называют расходящимся. Такой ряд суммы не имеет. Свойство 1. 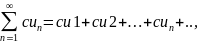Если ряд сходится и его сумма равна S, то ряд где с – произвольное число, также сходится и его сумма равна cS. Если же ряд расходится и с ≠ 0, то и ряд расходится. Свойство 2. Если сходится ряд 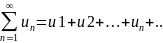и сходится ряд 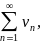а их суммы равны S1 и S2 соответственно, то сходятся и ряды причем сумма каждого равна соответственно S1 ± S2. Свойство 3. Если к ряду прибавить (или отбросить) конечное число членов, то полученный ряд и ряд сходятся или расходятся одновременно. Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число. Таким образом, геометрическая прогрессия – это числовая последовательность заданная соотношениямиb_n+1 =b_n · q, где b_n ≠ 0, q ≠ 0q – знаменатель прогрессии

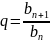
Геометрическая последовательность является возрастающей, если b1 > 0, q > 1,Геометрическая последовательность является убывающей, если b1 > 0, 0 < q < 1Формула n-го члена геометрической прогрессииb_n = b₁ · q _n-1Сумма n первых членов геометрической прогрессии равна: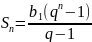

30. Числовым рядом называется выражение вида: где а1,а2,…,а_n,… - действительные или комплексные числа, называемые членами ряда, u_n – общим членом ряда. Сумма первых n членов ряда называется n-ой частичной суммой ряда и обозначается через S_n. Если существует конечный предел S = последовательности частичных сумм ряда, то этот предел называют суммой ряда.

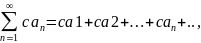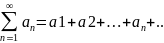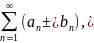31. Свойство 1. Если ряд сходится и его сумма равна S, то ряд где с – произвольное число, также сходится и его сумма равна cS. Если же ряд расходится и с ≠ 0, то и ряд расходится. Свойство 2. Если сходится ряд и сходится ряд а их суммы равны S1 и S2 соответственно, то сходятся и ряды причем сумма каждого равна соответственно S1 ± S2. Свойство 3. Если к ряду прибавить (или отбросить) конечное число членов, то полученный ряд1(a1+a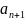2+ + )и ряд2(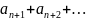 )сходятся или расходятся одновременно. Свойство 4. Сумму сходящегося ряда можно предст. В виде (частичной) суммы: част. Суммы ряда и его остатка. Свойство 5. Если ряд a1+a2+ + сходится, то его остатком после n-го члена »0, при n»∞. 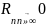.Необх. признак. 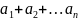Если ряд сходится, то его n-ый член стремится к 0, при n»∞, т.е.

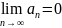
32. Если f(n)= на промежутке [1;+ ), является неубывающей, тогда ряд 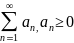и несобственный интеграл

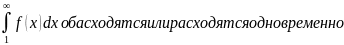
33. Теорема. Пусть даны два знакоположительных ряда 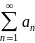и 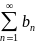. Если для всех n выполняется неравенство 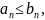то из сходимости ряда следует сходимость ряда , из расходимости первого ряда следует расходимость второго ряда. Теорема (предельный признак сравнения). Пусть даны два знакоположительных ряда и . Если существует конечный, отличный от 0, предел то ряды сходятся или расходятся одновременно.

36)Понятие степенного ряда. Область сходимости степенного ряда.

Степенным рядом наз: (1)n-ый член ряда u=a. 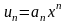числа наз. коэф. Ряда.Рассмотрим ряд более общего вида: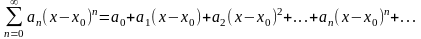 (1*)Ряд(1*) с помощью подстановки , можно свести к(1).поэтому изучение ряда(1*)сводится к изучению (1)Изучим ряд(1):Предавая х различные числовые значения, мы будем получать различные числ.ряды,кот могут оказаться как сходящимися так и расходящимися.Опр1 множество знач. Х при кот (1) сходится наз область сходимости. множество знач. Х при кот расходится наз. область расходимости. При х=0,(1) сходится 37)теорема Абеля.рассмотрим вопрос о структуре области сход. Степ рядатеорема Абеля:Пусть дан(1):1)если степ.ряд сход. При ,то он сход. Абсолютно при при всех довлетворяющих неравенство: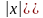 2)если ряд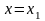 ,расход.то он расход. При всех 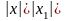замечание 1. для каждого(1) сущ такое число 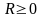,что в промежутке(-R;R) …?….(т.е. для всех х удовлет. неравенство ряд(1) сход. Абсолютно , а вне промежутка (-RR) , ряд расход.

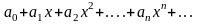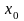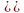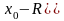
в т. R ряд может оказаться сход. и несход.Число R наз радиусом сход. А (-R;R) промежуток – интервалом сходЗамечание 2 центр интервала сход.(1*) нах. В т. .действительно х сход при всех х удовлет. Неравенство -R R , 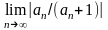т.о. всякий ряд имеет свой радиус сход. и интервал сход (-R;R). При х= R ряд может сход и расход. Следовательно областью сход (1) явл. Его интервал сход с возможным присоед. Им 1 или 2 точками, в зависимости от того как ведет себя ряд в интервале.

38)ряды Тейлора и Маклорена пусть f(x) определена на промежутке 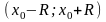. Сущ. такой степ ряд (1)сумма кот = f(x) на этом интревале. Если ряд сущ. , то говорят что f(x) на разлагается в (1). Т.е. имеет место разложениеf(x)= (2)теорема если на функция f(x) разлагается на степ. Ряды, т.е. имеет место равенство(2),то это разложение-ед.коэф.разложения опр.ондозначно по формуле

т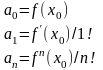 огда (2) перепишится след. Образом.:

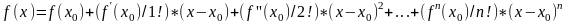(3)

опр ряд стоящий в правой части(3)= (4)

наз ряд Тейлора .если в ряде (3) , то получится

(5)

ряд маклое? Теорема f(x) на разлагается в степ ряд то этот ряд явл. Рядом тэйлораЕсли f(x) на диф. Любое число раз, то можно построить ряд однако может оказаться что ряд расход или сход не к той функции к кот построен.Ответ на вопрос при каких условиях ряд сход именно к той функции для кот он построен дает теорема:

(необходимый и достаточный признак разлож ф. в ряд тэйлора).Для того чтобы f(x) на разлаг на ряд,необходимо и достаточно что бы выполнялось равенство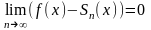 где n-ая частичная сумма ряда тэйлора.Разложение некот ф. в степ ряды.(ряд маклорена)

Вертикальные асимптоты. Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определения D(f), если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она не определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.

Наклонные и горизонтальные асимптоты. Если область определения D(f) вклоючает в себя лучи вида (a;+) или (−;b), то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при x+ или x− соответственно, т.е. найти limxf(x). Наклонные асимптоты: y = kx + b, где k=limx+xf(x) и b=limx+(f(x)−x). Горизонтальны асимптоты: y = b, где limxf(x)=b.

Нахождение точек пересечения графика с осями. Нахождение точки пересечения графика с осью Oy. Для этого нужно вычислить значение f(0). Найти также точки пересечения графика с осью Ox, для чего найти корни уравнения f(x) = 0 (или убедиться в отсутствии корней). Уравнение часто удается решить лишь приближунно, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.

Нахождение точек пересечения графика с асимптотой. В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой. Нахождение промежутков монотонности. Найти интервалы монотонности функции f(x) (то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной f(x). Для этого находят производную f(x) и решают неравенство f(x)0. На промежутках, где это неравенство выполнено, функция f(x) возрастает. Там, где выполнено обратное неравенство f(x)0, функция f(x) убывает.

Нахождение локального экстремума. Найдя интервалы монотонности, мы можем сразу определить точки локального экстремума там, где возрастание сменяется убыванием, располагаются локальные максимумы, а там, где убывание сменяется возрастанием -- локальные минимумы. Вычислить значение функции в этих точках. Если функция имеет критические точки, не являющиеся точками локального экстремума, то полезно вычислить значение функции и в этих точках.

Нахождение интервалов выпуклости и вогнутости. Это делается с помощью исследования знака второй производной f(x). Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции. Найдя f(x) , мы решаем неравенство f(x)0. На каждом из интервалов решения функция будет выпуклой вниз. Решая обратное неравенство f(x)0, мы находим интервалы, на которых функция выпукла вверх (то есть вогнута). Определяем точки перегиба как те точки, в которых функция меняет направление выпуклости (и непрерывна).

Нахождение наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b] (продолжение)1. Найти производную функции: f(x).2. Найти точки, в которых производная равна нулю: f(x)=0 x1, x2,...3. Определить принадлежность точек х1, х2, … отрезку [a; b]: пусть x1a;b , а x2a;b .4. Найти значения функции в выбранных точках и на концах отрезка: f(x1), f(x2),..., f(xa), f(xb),5. Выбор наибольшего и наименьшего значений функции из найденных.