19. Формула Ньютона-Лейбница.

Простым и удобным методом вычисления определенного интеграла от непрерывной функции является формула Ньютона-Лейбница: 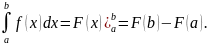Применяется этот метод во всех случаях, когда может быть найдена первообразная функции F(x) для подынтегральной функции f(x).

20.Интегрирование по частям в определенном интеграле.

1)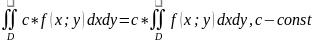 , 2) 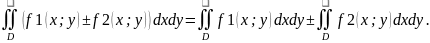3) Если область D разбить линией на две области D1 и D2 такие, что D1 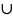D2 = D, а пересечение D1 и D2 состоит лишь из линии, их разделяющей, то: 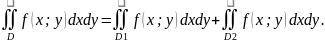4) Если в области D имеет место неравенство f(x;y) ≥ 0, то и 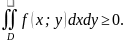Если в области D функции f(x;y) и g(x;y) удовлетворяют неравенству f(x;y) ≥ g(x;y), то и 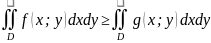. 5) 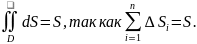6) Если функция f(x;y) непрерывна в замкнутой области D, площадь которой S, то mS ≤ 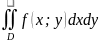≤ MS, где m и M – соответственно наименьшее и наибольшее значения подынтегральной функции в области D. 7) Если функция f(x;y) непрерывна в замкнутой области D, площадь которой S, то в этой области существует такая точка (x0;y0), что 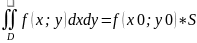. Геометрическийсмысл: Величина двойного интеграла от неотрицательной функции равна объему цилиндрического тела. (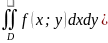

21. Площадь плоской фигуры, объем тела вращения, длина дуги кривой.

Пусть y=f(x) непрер и не отр на [a,b] . f(x)≥0Рассмотрим кривол трап, огранич графиками и прямыми x=a, x=b, y=0.S= , f(x)≥0Пусть y=f(x) не прерывна на [a,b] причем f(x)≤0

Рассмотрим кривол трап, образ графиком ф-ции x=a, x=b, y=0.

Для этого построим кривол трап граф ф-ции y= -f(x) и прям x=a, x=b, y=0 по данном f(x)≤0, тогда - f(x)≥0. Следов-но S1=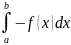 = 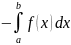.Т.к. трапеции aABb и aA’B’b конгруэнтны то их площади равны.S=S1 S= .

22. Несобственные интегралы с бесконечными пределами.

Пусть y=f (x) определ на промежут [а;+∞) и предположим тчо эта ф-ция интегрируема на [а;b], при любом b>a, т.е. сущ опред интеграл .Определение 1. Несобственным интегралом называют след предел 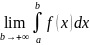. Если этот 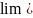сущ и конечен, то гов что несобствен интеграл сущ или сходится. В противном случае не сущ или расходится. Т. о. по определению интеграл 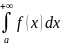= 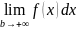. Аналогично определяются интегралы для др бесконечных промежутков

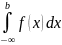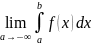Определение 2. = .(2)

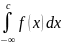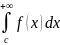Определение 3. = + .(3)

-∞<c<+∞

Исходный интеграл сходиться только тогда, когда сходятся оба интеграла, стоящие в правой части равенства (3).

23. Несобственные интегралы от неограниченных ф-ций.

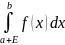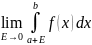Пусть y=f(x) определ [a,b] кроме может быть самой (.)а в окрестности которой она не ограничена.(.)а наз особой точной ф-ции f(x)Предположим что ф-ция f(x) интегрируема на некотором отрезке [а+Е;b] т.е. при таком Е сущ интеграл . Несоб интегралом назыв след предел . Если этот предел сущ или конечен ,то несоб интеграл сущ или сходится, в противном случае не сущ или расходится. Т.о. = .

Аналогично определ несоб интегралы, где b и c особые точки:

= .

= + .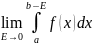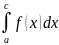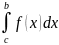