1.Основные теоремы о дифференцируемых функциях. Теорема Ролля. Пусть функция y=f(x) удовлетворяет следующим условиям:1. Непрерывна на отрезке [a, b];2. Дифференцируема на интервале (a, b);3. На концах отрезка принимает равные значения, т.е. f(a)=f(b).

Т огда внутри отрезка существует по крайней мере одна такая точка t∈(a, b), в которой производная функции равна нулю f’(t)=0. Теорема Лагранжа

Теорема. Пусть функция y=f(x) удовлетворяет следующим условиям:1. Непрерывна на отрезке [a, b];2. Дифференцируема на интервале (a, b);Тогда внутри отрезка существует по крайней мере одна такая точка с∈(a, b), в которой производная функции равна частному от деления приращения функции на приращение аргумента, т.е.:

Теорема Коши.Теорема. Пусть даны две функции y=f(x) и y=g(x) такие, что удовлетворяют следующим условиям:1. Определены и непрерывны на отрезке [a, b];

2. Дифференцируемы на интервале (a, b);3. Их производные не обращаются в ноль одновременно на интервале (a, b):4. g(a) ≠ g(b).

Тогда внутри отрезка существует по крайней мере одна такая точка с∈(a, b), в которой справедливо равенство:

2. Достаточные условия убывания и возрастания ф-ции

Теорема (достаточное условие возрастания функции): Если производная дифференцируемой функции положительна внутри некоторого промежутка Х, то она возрастает на этом промежутке.

Доказательство: Рассмотрим два значения х1 и х2 на данном промежутке Х. Пусть х1 > х2; (х1, х2)ϵХ. Докажем, что f(х1) > f(х2). Для функции f(х) на отрезке [х1, х2] выполняются условия теоремы Лагранжа, поэтому:f(x2) - f(x1) = f’(t)(x2 – x1), где x1<t<x2, т.е. t принадлежит промежутку, на котором производная положительна, отсюда следует, что f’(t)>0, а значит f’(t)(x2 – x1)>0Отсюда следует, что f(x2) - f(x1)>0, значит f(x2) > f(x1)Теорема (достаточное условие убывания функции): Если производная дифференцируемой функции отрицательна внутри некоторого промежутка Х, то она убывает на этом промежутке.Доказательство аналогично предыдущему.

3. Экстремум функции.

Определение 1: Точка х0 называется точкой максимума функции f(x), если в некоторой окрестности х0 выполняется неравенство f(x)≤ f(x0).Определение 2: Точка х0 называется точкой минимума функции f(x), если в некоторой окрестности х1 выполняется неравенство f(x)≥f(x1):

З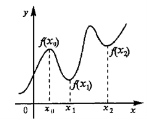 начения функции в точках х0 и х1 называются соответственно максимумом и минимумом функции или объединяются общим названием – экстремум функции.Необходимое условие экстремума: Для того, чтобы функция f(x) имела экстремум в точке х0, необходимо, чтобы ее производная в этой точке равнялась нулю (f’(x0)=0) или не существовала.Такие точки называются критическими. Чтобы функция имела экстремум в точке, точка должна быть критической, но не всякая критическая точка является точкой экстремума.Первое достаточное условие экстремума: Если при переходе через точку х0 производная дифференцируемой функции y=f(x) меняет свой знак с плюса на минус, то точка x0 есть точка максимума функции y=f(x), а если с минуса на плюс – то точка минимума.Второе достаточное условие экстремума: Если первая производная f’(x) дважды дифференцируемой функции равна нулю в некоторой точке x0, а вторая производная в этой точке f’’(x0) положительна, то точка x0 есть точка минимума функции f’(x), а если f’’(x0) отрицательна, то x0 - точка максимума.

4. Выпуклость функции. Точки перегиба.

Определение 1. Функция y=f(x) называется выпуклой вниз (или вогнутой) на промежутке Х, если для любых двух значений (х₁, х₂)∈Х из этого промежутка выполняется неравенство:

О пределение 2. Функция y=f(x) называется выпуклой вверх на промежутке Х, если для любых двух значений (х₁, х₂)∈Х из этого промежутка выполняется неравенство:

Т еорема 1. Функция выпукла вниз (вверх) на промежутке Х тогда и только тогда, когда ее первая производная на этом промежутке монотонно возрастает (убывает).Теорема 2. Если вторая производная дважды дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка Х, то функция выпукла вниз (вверх) на этом промежутке.Определение 3. Точкой перегиба графика непрерывной функция называется точка, разделяющая интервалы, в которых функция выпукла вверх и вниз.

Теорема 3 (необходимое условие перегиба). Вторая производная f’’(x) дважды дифференцируемой функции в точке перегиба равна нулю, т.е. f’’(x)=0.Теорема 4 (достаточное условие перегиба). Если вторая производная f’’(x) дважды дифференцируемой функции при переходе через некоторую точку х₀ меняет свой знак, то точка х₀ есть точка перегиба ее графика.