1. Дифференциальное уравнение оси изогнутого бруса. Интегрирование дифференциального уравнения при наличии одного или нескольких участков загружения балки.

Уравнение изогнутого бруса:

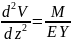
Правила интегрирования:

- начало координат всегда брать в одной точке (крайне левой) и при рассмотрении моментов рассматривать левую часть балки;

- продолжать распределенную нагрузку до конца балки и при необходимости прикладывать компенсирующую нагрузку;

- интегрирование производить не раскрывая скобок;

- момент брать с множителем z (расстояние от начала координат до точки приложения моментов).

Интегрирование для одного участка: , , ,

,

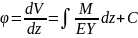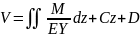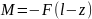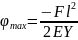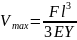
При интегрировании бруса с несколькими участками нагружения достаточно записать уравнения момента для последнего участка, поставив ограничители по участкам:

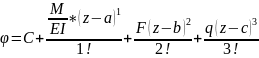
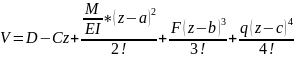
С и D находятся из граничных условий (условий закрепления балки).

2. Перемещения в балках при изгибе. Порядок расчета методом начальных параметров.

Одной из задач сопротивления материалов является оценка жесткости конструкции, т.е. степени ее искажения под действием нагрузки. Если балка под нагрузкой сильно прогибается, то при ее эксплуатации появятся затруднения.

Метод начальных параметров

Ход решения:

- определить реакции (кроме заделок)

- записать два уравнения методом начальных параметров для своей балки, соблюдая правила:

а) начало координат всегда брать в одной точке (крайне левой) и при рассмотрении моментов рассматривать левую часть балки;

б) продолжать распределенную нагрузку до конца балки и при необходимости прикладывать компенсирующую нагрузку.

- определить начальные параметры из граничных условий (рис2)

- определить перемещение в заданной точке путем подстановки в уравнение вместо z расстояние от начала координат до заданной точки. Учитывать только тот участок, которому принадлежит данная точка.

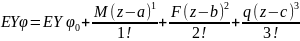
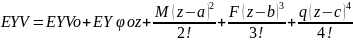
3. Интеграл Мора. Определение перемещений с его помощью.

Интеграл Мора: 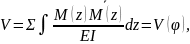где

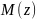– аналитическое выражение изгибающего момента от всей внешней нагрузки,

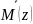– аналитическое выражение изгибающего момента от единичного фактора в том же сечении z.

Для определения линейного перемещения к данной точке прикладывается единичная сила, а вся остальная внешняя нагрузка убирается.

Для определения углового перемещения к данному сечению прикладывается единичный момент, а вся внешняя нагрузка убирается.

Если результат получился со знаком “-”, то точка перемещается против направления единичного фактора.

Пример

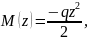
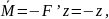
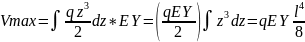
4. Определение перемещений в балках по формулам Верещагина и Симпсона.

Формула Верещагина: 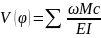I, где ω – площадь грузовой эпюры, Mc – ордината единичной эпюры, взятая под центром тяжести грузовой эпюры.

Если эпюры построены с разных сторон, при перемножении учитывать знак -.

Формулой Верещагина удобно пользоваться, если простая геом. Фигура.

Формула Симпсона-Карнаухова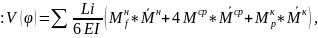 где Li – длина участка, Mf и 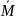– значения моментов с грузовой и единичной эпюр, взятые в начале, середине и конце участка.

5. Расчет статически неопределимых балок при изгибе. Раскрытие статической неопределимости.

Если число опорных реакций в балке превышает число уравнений статики, то такая задача называется статистически неопределимой.

Статическая неопределимость: n=R-Ш-3, где R – число всех реакций, Ш – число простых шарниров, 3 уравнения статики.

Мы решаем один раз статически неопределимую балку:

1) определить n;

2) выбрать основную систему, путем отбрасывания лишней связи;

Требование к осн. системе: она должна быть статистически неопределимой и геометрически неизменяемой.

- зарисовать эквивалентную систему: к основной системе приложить всю внешнюю нагрузку и вместо отброшенной связи приложить неизвестную реакцию;

- разложить эквивалентную систему на две: а)балка от всей внешней нагрузки, б)балка от неизвестной реакции;

- в балке а любым методом найти перемещение Vf - перемещение от всей внешней нагрузки по направлению отброшенной связи: ;

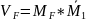- в балке б любым методом найти перемещение Vr - перемещение от неизвестной реакции в этой же точке по направлению отброшенной связи ;

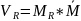- из условия Vf+Vr=0 найти неизвестную реакцию ;

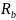- вернуться к исходной балке, пририсовать найденную реакцию, найти остальные реакции и построить эпюры Q и M;

-сделать деформационную проверку, которая показывает, что перемещение в точке В (перемещение по направлению отброшенной связи) должно быть =0.