Удельное скольжение

Удельным скольжением называется отношение скорости скольжения профилей в точке их касания к скорости перемещения точки касания по профилю. Этот показатель характеризует износ зубьев в результате трения скольжения их боковых (рабочих) поверхностей. Возьмём точки К₁ первого профиля и К₂ второго профиля, с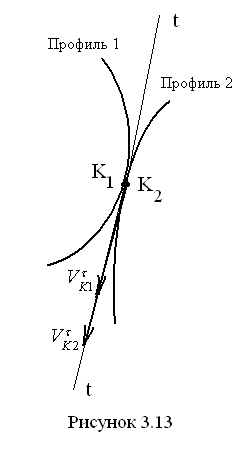 овпадающие в данный момент друг с другом (рис. 3.13). В этих точках профили имеют общую касательную t – t, вдоль которой направлены касательные (тангенциальные) составляющие их абсолютных скоростей. В общем случае эти скорости отличаются друг от друга по величине, могут отличаться и по направлению, оставаясь на общей касательной. Разность величин этих скоростей составляет скорость скольжения в контакте зубьев.

Согласно определению, удельное скольжение выразится двумя математическими выражениями, относящимися к разным колёсам:

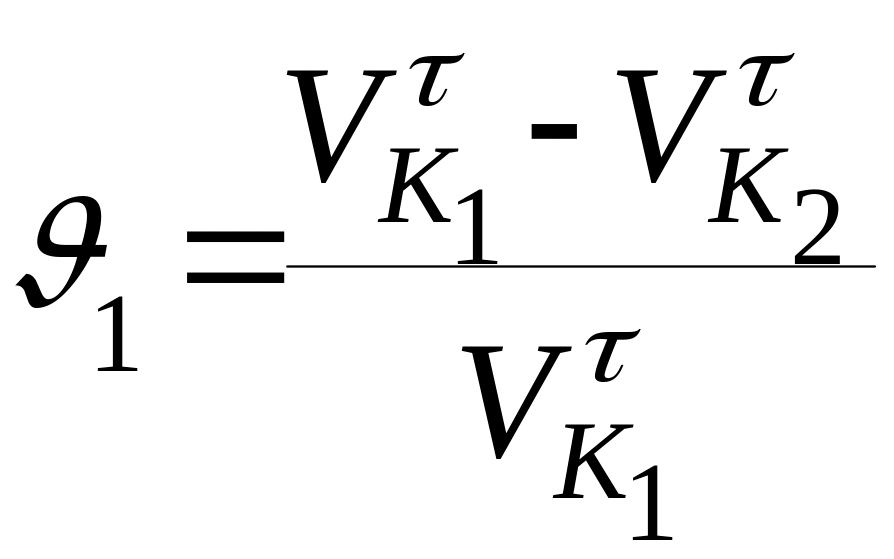и .

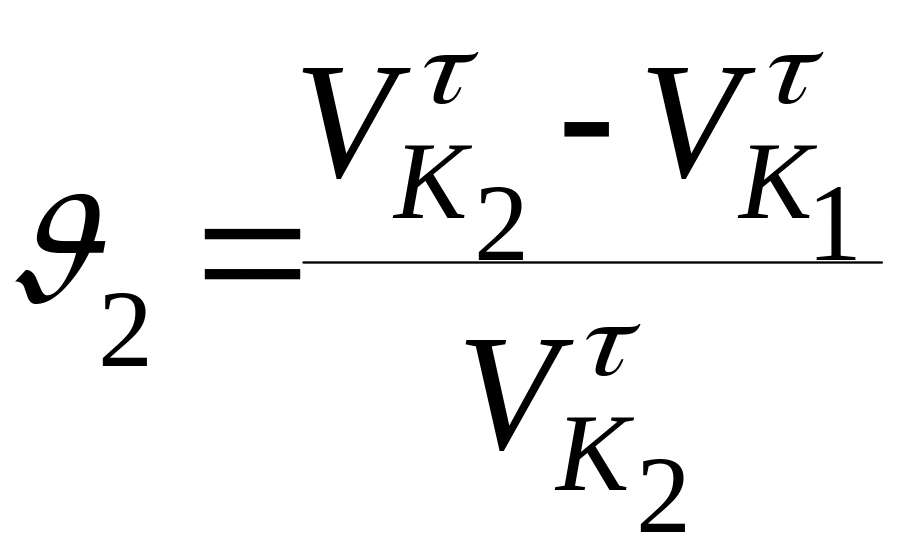Для определения тангенциальных составляющих скоростей обратимся к

рис. 3.14. Соединим точку К₁ с центром О₁ вращения колеса 1 радиусом R₁, и точку К₂, совпадающую с точкой К₁, с центром О₂ радиусом R₂. Перпендикулярно радиусу R₁ в сторону вращения колеса 1 отложим абсолютную скорость точки К₁, равную , и перпендикулярно радиусу R₂ в сторону вращения колеса 2 отложим абсолютную скорость точки К₂, равную . Отметим угол β₁ между радиусом R₁ и перпендикуляром O₁N₁ к линии зацепления и β₂ между радиусом R₂ и перпендикуляром О₂N₂ также к линии зацепления. Спроецируем скорости и на линию зацепления N₁N₂. Линия зацепления направлена по нормали к профилям зубьев, поэтому проекции скоростей на неё являются нормальными составляющими, равными друг другу. Составляющие, направленные перпендикулярно линии зацепления, действуют по касательной к профилям и являются тангенциальными составляющими. Они определяются следующими цепоч-

ками преобразований

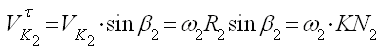
C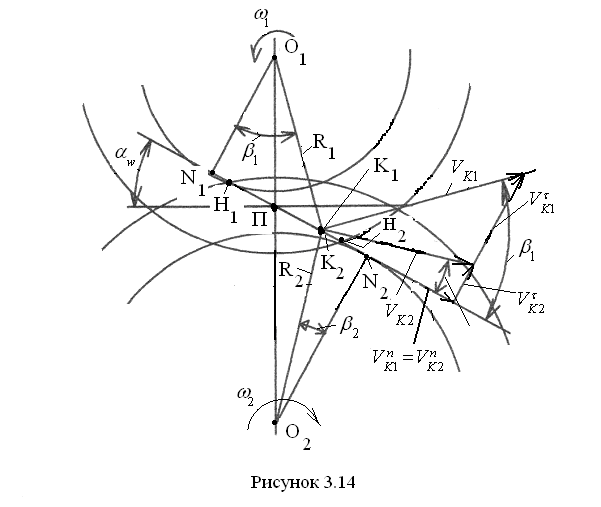 учётом этого ранее записанные выражения примут следующий вид:

, .

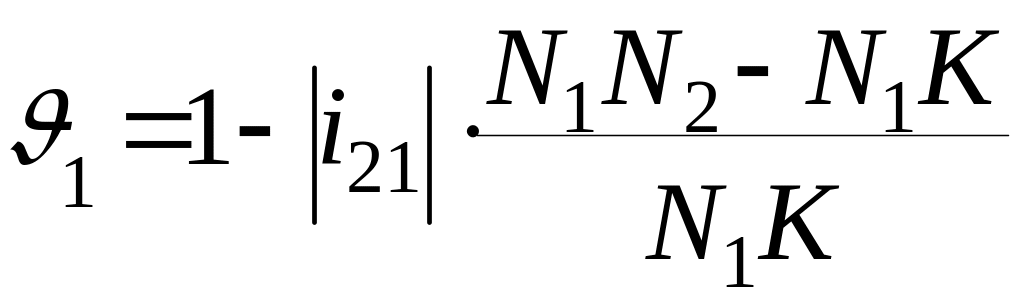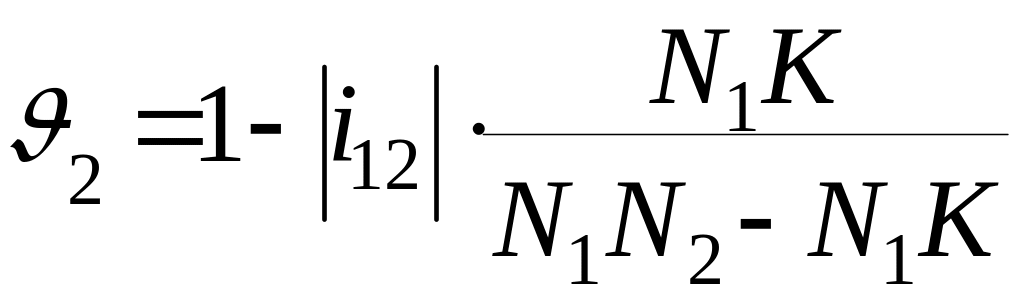В этих выражениях буквой К обозначены совпадающие друг с другом точки К₁ и К₂. Схематический график удельного скольжения показан на рис. 3.15.

Г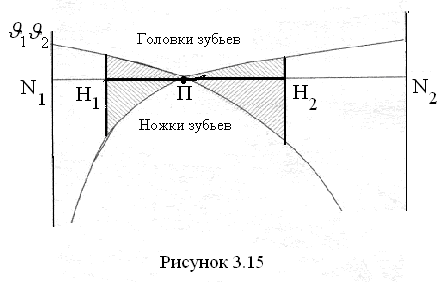 рафик показывает, что удельное скольжение на головках зубьев меньше чем на ножках, следовательно, ножки изнашиваются интенсивнее, чем головки. Характер износа таков, что чем дальше от полюса в радиальном направлении находится зона профиля, тем больше она изнашивается. В полюсе зацепления износ от скольжения равен нулю, так как эта точка является мгновенным центром поворота одного колеса относительно другого, и точки профилей, попадающие в полюс, имеют радиус относительного вращения вокруг полюса, равный нулю.

Коэффициент удельного давления

Коэффициентом удельного давления называется отношение модуля зацепления к приведённому радиусу кривизны профилей зубьев в точке их контакта. Этот коэффициент применяется при расчёте зубьев на контактную прочность. Формула Герца для расчёта контактных напряжений в контакте двух цилиндров имеет вид

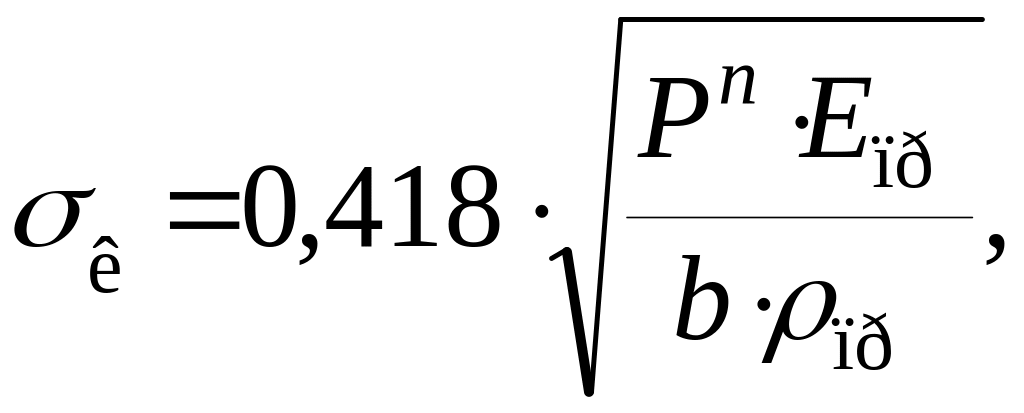
где –нормальное усилие, сжимающее цилиндры, – приведённый модуль упругости, – длина контактной линии цилиндров, – приведённый радиус кривизны цилиндров.

Умножив числитель и знаменатель формулы на модуль , не изменим результат, а формула Герца приобретёт следующий вид

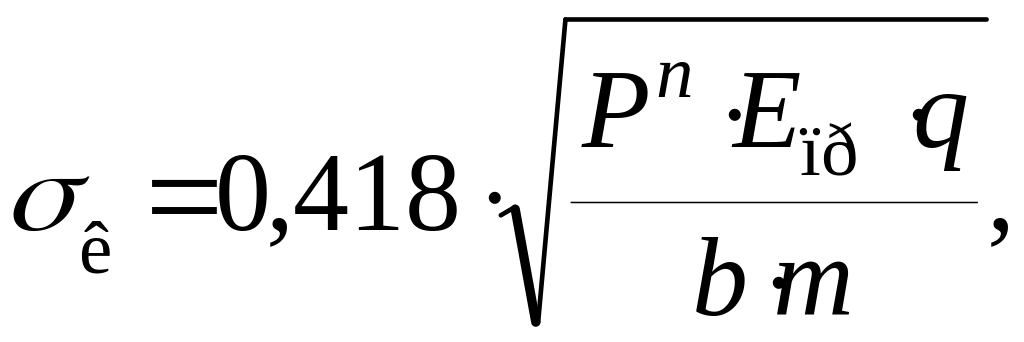
где 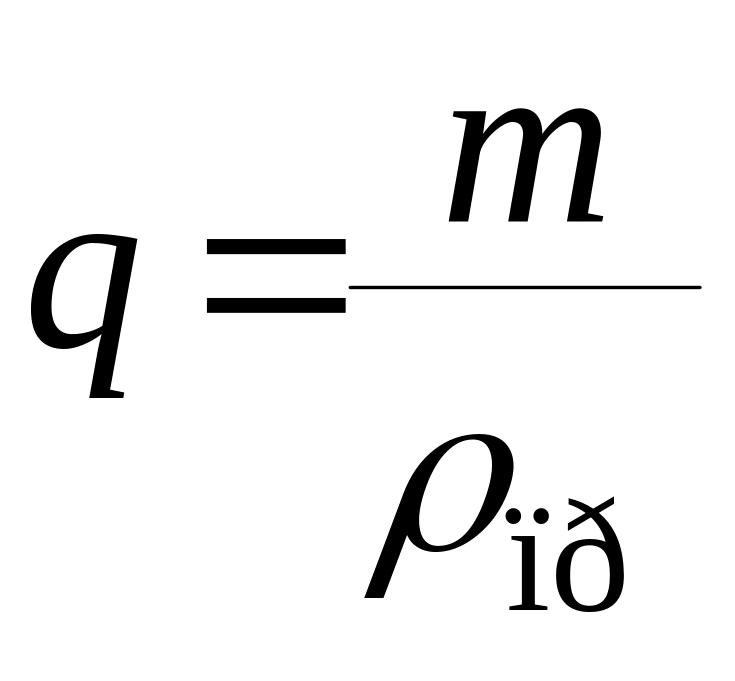и представляет собой коэффициент удельного давления.

П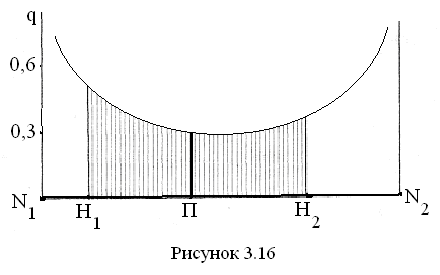 риведённый радиус кривизны определяется как величина, обратная приведённой кривизне, равная сумме кривизн контактирующих профилей, т. е. .

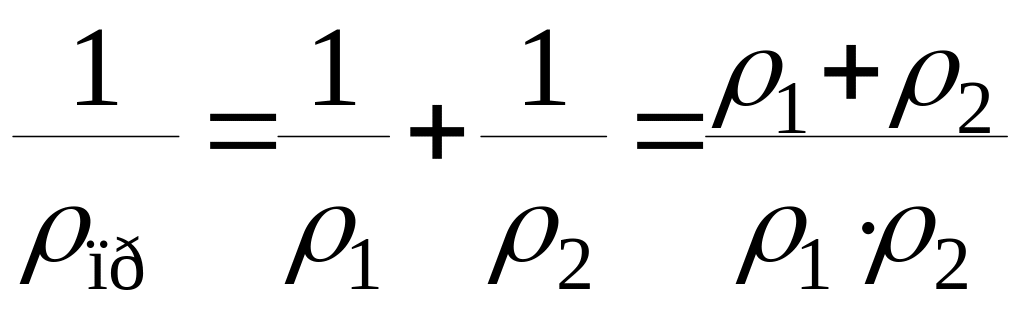На основании свойств эвольвенты радиусы кривизны профилей равны: и , поэтому окончательно формула получится в виде

.

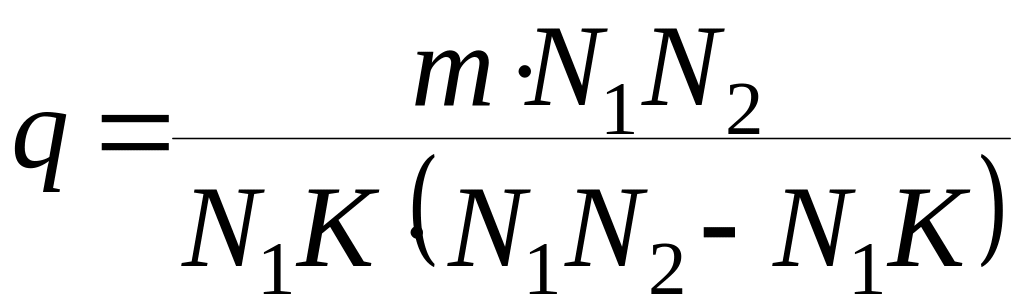Примерный вид графика коэффициента удельного давления в зависимости от положения точки контакта на линии зацепления показан на рис. 3.16.