
- •1. Сложение матриц и умножение матрицы на число.
- •2. Умножение матриц. Невырожденные квадратные матрицы.
- •3. Обратная матрица. Алгоритм нахождения обратной матрицы.
- •4. Решение матричных уравнений вида , .
- •5. Определители и их свойства.
- •6. Непосредственное вычисление определителей второго и третьего порядков.
- •7. Формула разложения определителя по строкам и столбцам. Теорема Лапласа.
- •8. Ранг матрицы. Нахождение ранга матрицы.
- •9. Системы линейных алгебраических уравнений.
- •10. Решение систем линейных алгебраических уравнений методом Гаусса.
- •11. Нахождение решения системы линейных алгебраических уравнений по формуле Крамера.
- •12. Нахождение решения системы линейных алгебраических уравнений методом обратной матрицы.
- •14. Теорема Кронекера-Капелли.
- •15. Арифметические векторы и линейные операции над ними.
- •16. Линейная зависимость системы векторов.
- •17. Базис и размерность линейного пространства. Координаты вектора в данном базисе.
- •22. Схема Горнера и корни многочленов.
- •23. Теорема Безу. Нод многочленов и алгоритм Евклида.
- •24. Комплексные числа и действия над ними.
- •25. Геометрическая интерпретация комплексных чисел. Модуль и аргумент комплексного числа.
- •26. Алгебраическая и тригонометрическая формы записи комплексных чисел.
- •27. Корни n-ой степени из комплексного числа.
- •28. Линейные преобразования пространства . Линейные операторы.
- •29. Матрица линейного оператора.
- •30. Собственные значения и собственные векторы линейных операторов.
- •31. Собственные значения квадратных матриц.
- •32. Квадратичные формы, их матрицы в данном базисе.
- •33. Приведение квадратичной формы к нормальному виду методом Лагранжа.
- •34. Приведение квадратичной формы к каноническому виду при помощи ортогонального преобразования.
- •35. Закон инерции квадратичных форм.
- •36. Критерий Сильвестра знакоопределенности квадратичных форм.
- •37. Уравнение плоскости, проходящей через данную точку.
- •38. Общее уравнение плоскости и его исследование.
- •39. Уравнение плоскости, проходящей через три данные точки.
- •40. Угол между двумя плоскостями. Условия параллельности и перпендикулярности.
- •41. Общее уравнение прямой на плоскости и его исследование.
- •42. Уравнение прямой в отрезках.
- •43. Уравнение прямой с угловым коэффициентом.
- •44. Уравнение прямой, проходящей через данную точку в заданном направлении.
- •45. Угол между двумя прямыми на плоскости. Условие параллельности и перпендикулярности прямых.
- •46. Виды уравнения прямой: векторное, параметрическое и каноническое уравнения прямой в пространстве.
- •47. Уравнение прямой в пространстве, проходящей через две данные точки.
- •48. Прямая как линия пересечения двух плоскостей.
- •49. Окружность. Определение. Каноническое уравнение.
- •50. Эллипс. Определение. Каноническое уравнение. Свойства.
- •51. Гипербола. Определение. Каноническое уравнение. Свойства.
- •52. Парабола. Определение. Каноническое уравнение. Свойства.
41. Общее уравнение прямой на плоскости и его исследование.
Для
получения общего уравнения прямой на
плоскости вспомним само уравнение
плоскости:
.
Найдем линию пересечения плоскости с
одной из координатных плоскостей,
например с плоскостью x0y.
Для этого решим систему:
 .
.
 – общее уравнение прямой на x0y.
Исследуем это уравнение: 1) D=0:
Ax+By=0
=>
– общее уравнение прямой на x0y.
Исследуем это уравнение: 1) D=0:
Ax+By=0
=>
 – прямая проходит через начало координат.
2) B=0:
Ax+D=0
=>
– параллельно 0y.
3) A=0:
By+D=0
=>
– прямая проходит через начало координат.
2) B=0:
Ax+D=0
=>
– параллельно 0y.
3) A=0:
By+D=0
=>
 – параллельно 0x.
4) A=D=0;
By=0
=> y=0
– ось x.
5) B=D=0,
Ax=0
=> x=0
– ось 0y.
– параллельно 0x.
4) A=D=0;
By=0
=> y=0
– ось x.
5) B=D=0,
Ax=0
=> x=0
– ось 0y.
42. Уравнение прямой в отрезках.
Пусть
дано общее уравнение прямой на плоскости
.
Преобразуем его:
 .
Это
уравнение прямой в отрезках. A
и b
– отрезки, которые отсекает прямая на
координатных осях.
.
Это
уравнение прямой в отрезках. A
и b
– отрезки, которые отсекает прямая на
координатных осях.
43. Уравнение прямой с угловым коэффициентом.
Положение
прямой на плоскости вполне определяется
заданием угла α, образованного прямой
с положительным направлением оси абсцисс
и величиной отрезка b,
отсекаемым от оси 0y.
Прямая на плоскости имеет два параметра:
α и β. Величина
 называется угловым коэффициентом
прямой.
называется угловым коэффициентом
прямой.

Через
точку пересечения прямой l
с 0y
проведем прямую, параллельную 0x.
На прямой l
возьмем произвольную точку M
и опустим из нее перпендикуляр на ось
абсцисс. Рассмотрим ∆MKN.
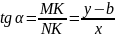 ,
,
 – уравнение прямой с угловым коэффициентом.
– уравнение прямой с угловым коэффициентом.
44. Уравнение прямой, проходящей через данную точку в заданном направлении.
Пусть
прямая проходит через точку
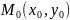 .
По условию задано направление, значит
известен угловой коэффициент k.
Требуется найти уравнение прямой l.
Т. к. точка
принадлежит этой прямой, то ее координаты
удовлетворяют уравнению прямой
.
По условию задано направление, значит
известен угловой коэффициент k.
Требуется найти уравнение прямой l.
Т. к. точка
принадлежит этой прямой, то ее координаты
удовлетворяют уравнению прямой
 .
Получим:
.
Получим:
 Вычтем из (2) уравнение (1):
Вычтем из (2) уравнение (1):
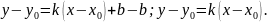 Это уравнение называется уравнением
прямой, проходящей через данную точку
в заданном направлении.
Это уравнение называется уравнением
прямой, проходящей через данную точку
в заданном направлении.
45. Угол между двумя прямыми на плоскости. Условие параллельности и перпендикулярности прямых.
Углом
между двумя прямыми
 и
и
 на плоскости называется угол, на который
нужно повернуть прямую
относительно точки пересечения этих
прямых против часовой стрелки до
совпадения с прямой
.
Построим две прямые в системе координат
на плоскости.
на плоскости называется угол, на который
нужно повернуть прямую
относительно точки пересечения этих
прямых против часовой стрелки до
совпадения с прямой
.
Построим две прямые в системе координат
на плоскости.
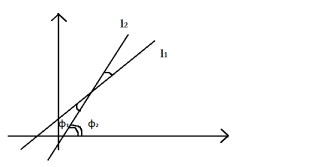
 (1).
Формула (1) определяет угол между двумя
прямыми на плоскости.
(1).
Формула (1) определяет угол между двумя
прямыми на плоскости.
Условие
параллельности:
 (2).
Из (2) следует, что если прямые параллельны,
то их угловые коэффициенты равны. Если
уравнения прямых заданы в общем виде,
тогда:
(2).
Из (2) следует, что если прямые параллельны,
то их угловые коэффициенты равны. Если
уравнения прямых заданы в общем виде,
тогда:
 Из
(2) следует, что чтобы прямые были
параллельны, должно выполняться:
Из
(2) следует, что чтобы прямые были
параллельны, должно выполняться:
 Условие перпендикулярности имеет вид
Условие перпендикулярности имеет вид
 (3). Из (3) следует, что если прямые
перпендикулярны, то их угловые коэффициенты
обратны по величине и противоположны
по знаку.
(3). Из (3) следует, что если прямые
перпендикулярны, то их угловые коэффициенты
обратны по величине и противоположны
по знаку.
46. Виды уравнения прямой: векторное, параметрическое и каноническое уравнения прямой в пространстве.
Положение
прямой в пространстве определено, если
на прямой задана точка
 и вектор
и вектор
 ,
параллельный прямой или лежащий на ней.
Вектор
называется направляющим вектором этой
прямой. Задать вектор – значит задать
его координаты, т. е. проекции на оси
координат. Направляющий вектор
имеет координаты
,
параллельный прямой или лежащий на ней.
Вектор
называется направляющим вектором этой
прямой. Задать вектор – значит задать
его координаты, т. е. проекции на оси
координат. Направляющий вектор
имеет координаты
 .
.
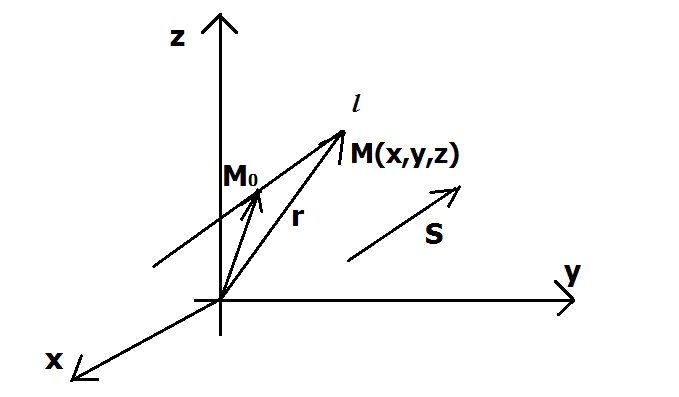
Вектор
 .
Он коллинеарен направляющему вектору
,
поэтому
.
Он коллинеарен направляющему вектору
,
поэтому
 ,
где
,
где
 - скалярный множитель, называемый
параметром, он может принимать любые
значения в зависимости от положения
точки M
на прямой. Проведем радиус-векторы к
точкам
и
- скалярный множитель, называемый
параметром, он может принимать любые
значения в зависимости от положения
точки M
на прямой. Проведем радиус-векторы к
точкам
и
 .
.
 .
Найдем
.
Найдем
 .
C
учетом полученных равенств перепишем
(1) в виде
.
C
учетом полученных равенств перепишем
(1) в виде
 (2). Уравнение (2) называется векторным
уравнением прямой. Оно показывает, что
каждому значению параметра соответствует
радиус-вектор некоторой точки, лежащей
на прямой. Представим (2) в координатной
форме:
(2). Уравнение (2) называется векторным
уравнением прямой. Оно показывает, что
каждому значению параметра соответствует
радиус-вектор некоторой точки, лежащей
на прямой. Представим (2) в координатной
форме:
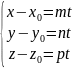 или
или
 (3). Уравнение (3) называется параметрическим
уравнением прямой. При изменении
параметра t
изменяются координаты x,
y
и z,
и точка M
движется по прямой. Из (3) можно найти
параметр t:
(3). Уравнение (3) называется параметрическим
уравнением прямой. При изменении
параметра t
изменяются координаты x,
y
и z,
и точка M
движется по прямой. Из (3) можно найти
параметр t:


 .
.
 Уравнение (4) называется каноническим
уравнением прямой линии в пространстве.
Уравнение (4) называется уравнением
прямой, проходящей через точку
с направляющим вектором
.
Уравнение (4) называется каноническим
уравнением прямой линии в пространстве.
Уравнение (4) называется уравнением
прямой, проходящей через точку
с направляющим вектором
.
