14. Теорема Кронекера-Капелли.
Системе
m
линейных уравнений с n
неизвестными можно сопоставить две
матрицы: основную
и расширенную
.
Матрица
состоит из коэффициентов при неизвестных,
а матрица
дополнена еще столбцом свободных членов.
Теорема
Кронекера-Капелли.
Система линейных уравнений совместна
тогда и только тогда, когда ранг
расширенной матрицы равен рангу основной
матрицы:
.
Рангом совместной системы линейных
уравнений называется ранг ее матрицы.
Если ранг системы равен числу переменных,
то система имеет единственное решение;
если ранг меньше числа неизвестных, то
система неопределенная и имеет
бесчисленное множество решений.
15. Арифметические векторы и линейные операции над ними.
N-мерным
арифметическим вектором
называется упорядоченная совокупность
n
действительных чисел, записываемых в
виде
,
где
- i-я
компонента, или координата, вектора
.
Операции
над векторами:
умножение вектора на число
(
)),
сложение двух векторов (
)).
16. Линейная зависимость системы векторов.
Система
векторов
называется линейно
зависимой,
если существуют такие числа
не равных нулю одновременно, что
Если система векторов такова, что это
равенство возможно только при
,
то эта система называется линейно
независимой.
17. Базис и размерность линейного пространства. Координаты вектора в данном базисе.
Базисом
линейного
пространства
L
называется любая система векторов
данного пространства, удовлетворяющая
условиям: 1) векторы этой системы линейно
независимы; 2) каждый вектор пространства
L
линейно выражается через векторы данной
системы. Размерностью
линейного
пространства
L
называется число векторов его базиса.
Обозначение:
Пусть
– базис пространства L
(
).
Тогда любой вектор
может быть записан в виде:
Это выражение называется разложением
вектора
по базису
,
т. е. числа
называются
координатами
вектора
в базисе
.
Обозначение:
18.
Скалярное произведение векторов в
Скалярное
произведение векторов
и
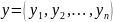в
n-мерном
арифметическом векторном пространстве
обозначается
и вычисляется по формуле:
.
Свойства:
1)
2)
.
3) (
.
4)
если
,
если
.
19. Евклидово пространство.
Евклидовым
пространством
называется векторное пространство, в
котором задано скалярное произведение
векторов, удовлетворяющее свойствам:
1)
2)
.
3) (
.
4)
если
,
если
.
Произвольное евклидово пространство
часто обозначают буквой
или
,
индекс n
указывает размерность пространства.
20. Неравенство Коши-Буняковского.
Для
любых двух векторов x,
y
евклидова пространства Е справедливо
неравенство
Коши-Буняковского:
или
.
При этом первое неравенство имеет место
тогда и только тогда, когда векторы x,
y
линейно зависимы.
21. Длины векторов и угол между векторами в .
Длиной
(нормой) вектора
в евклидовом пространстве называется
квадратный корень из скалярного квадрата
этого вектора:
.
В частности, в пространстве
длина вектора
определяется по формуле:
.
Углом
между ненулевыми векторами x
и y
евклидова пространства называется
угол
,
удовлетворяющий условиям:
и
.
В частности, в пространстве
угол между векторами
и
может быть найден по формуле:
.