1. Сложение матриц и умножение матрицы на число.
Произведением
матрицы А на число λ называется матрица
В=λа, элементы которой равны
.
Складываются матрицы поэлементно.
Разностью матриц А и В называется матрица
С, равная А+(-В).
2. Умножение матриц. Невырожденные квадратные матрицы.
Умножение
матриц
А и В определено, когда число столбцов
первой матрицы равно числу строк второй.
Тогда произведением матриц
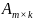и
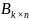является
.
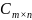Матрица С такая, что каждый ее элемент
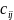равен сумме произведений элементов
i-ой
строки матрицы А на соответствующие
элементы j-го
столбца матрицы В. Произведение матриц
неперестановочно:
.
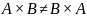Если
определитель матрицы
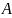равен нулю, то эта матрица называется
вырожденной,
если
,
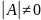то невырожденной.
3. Обратная матрица. Алгоритм нахождения обратной матрицы.
Матрица
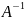называется обратной
по отношению к квадратной матрице
,
если при умножении этой матрицы на
данную матрицу как справа, так и слева
получается единичная матрица:
.
Если определитель матрицы
равен нулю, то матрица называется
вырожденной, если
,
то невырожденной. Алгоритм
нахождения обратной матрицы:
1) найти определитель матрицы и убедиться,
что он отличен от нуля; 2) каждый элемент
матрицы
заменить его алгебраическим дополнением,
получив присоединенную матрицу; 3)
транспонировать присоединенную матрицу;
4)
.
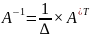4. Решение матричных уравнений вида , .
Обратная
матрица позволяет найти решения следующих
матричных уравнений:
,
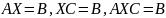где
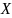– неизвестная матрица, А, В и С – некоторые
заданные матрицы, причем А и С имеют
обратные матрицы. Решением этих уравнений
являются соответственно матрицы
.
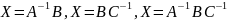5. Определители и их свойства.
Каждой
квадратной матрице А порядка n
ставится в соответствие по определенному
закону некоторое число, называемое
определителем
(детерминантом)
n-го
порядка. Обозначения:
.
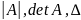Основные
свойства
определителей: 1) определитель не меняется
при транспонировании матрицы; 2) если
одна из строк (столбцов) определителя
состоит из нулей, то определитель равен
нулю; 3) определитель, содержащий две
одинаковые или пропорциональные строки
(столбца), равен нулю; 4) при перестановке
двух строк (столбцов) определитель
меняет знак; 5) общий множитель элементов
любой строки (столбца) можно вынести за
знак определителя; 6) величина определителя
не изменится, если к одной из строк
(столбцов) прибавить другую строку
(столбец), умноженную на любое число; 7)
если элементы какой-либо строки (столбца)
представлены в виде суммы двух слагаемых,
то определитель можно представить в
виде суммы двух определителей.
6. Непосредственное вычисление определителей второго и третьего порядков.
.
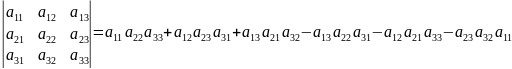7. Формула разложения определителя по строкам и столбцам. Теорема Лапласа.
Определитель
квадратной матрицы равен сумме
произведений элементов любой строки
(столбца) на их алгебраические дополнения:
.
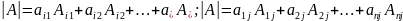Эти равенства называют разложениями
определителя
по i-ой
строке или по j-му
столбцу соответственно. Они принимают
особенно простой вид, если в строке или
столбце все элементы равны нулю, кроме
одного:
.
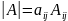