
- •1. Дувп. Решение. Общее решение. Общий интеграл. Промежуточный интеграл. Первый интеграл. Понижение порядка с помощью независимых первых интегралов.
- •2. Дувп. Задача Коши. Теорема Коши-Пикара. Теорема Пеано. Краевая задача.
- •3. Дувп. Неполные уравнения, интегрируемые в квадратурах.
- •4. Дувп. Неполные уравнения, допускающие понижение порядка.
- •5. Полные уравнения, допускающие понижения порядка.
- •6. Линейные дувп. Задача Коши. Т. Коши-Пикара. Однородные и неоднородные уравнения. Некоторые свойства решений лоду. Линейная независимость системы функций. Определитель Вронского.
- •7. Линейная независимость частных решений лоду n-го порядка. Формула Остроградского-Лиувилля.
- •8. Линейные ду n-го порядка. Фср. Теорема об общем решении лоду.
- •9. Задача о построении лоду по заданной фср.
- •10. Лоду n-го порядка с постоянными коэффициентами. Т. Коши-Пикара. Метод Эйлера построения фср. Случай простых корней характеристического уравнения.
- •11. Лоду n-го порядка с ПостК. Метод Эйлера построения фср. Случай кратных корней характеристического уравнения. Теорема об интегрируемости.
- •12. Лнду n-го порядка. Т. О структуре ор. Нек. Св-ва решений. Принцип суперпозиции.
- •13. Лнду n-го порядка. Метод Лагранжа вариации произвольных постоянных для отыскания чр. Т. Об интегрируемости.
- •14. Метод Коши отыскания чр лнду n-го порядка.
- •15. Лнду n-го порядка с ПостК и специальной правой частью (спч) вида .Метод неопределенных коэффициентов.
- •16. Лнду с ПостК и спч вида . Метод неопределенных коэффициентов.
- •17. Лнду с ПостК и спч вида . Метод неопределенных коэффициентов. Метод комплексных амплитуд.
- •18. Гармонический осциллятор под действием внешней гармонической силы. Явление резонанса.
- •19. Линейный осциллятор под действием внешней гармонической силы.
- •20. Лоду n-го порядка с ПеремК. Приведение к лду с ПостК с помощью замены аргумента.
- •21. Оду Эйлера.
- •22. Лоду n-го порядка с ПеремК. Приведение к лду с ПостК с помощью замены искомой функции.
- •23. Понижение порядка лоду n-го порядка с ПеремК при помощи известного частного решения.
- •24. Отыскание чр лоду n-го порядка с ПеремК в виде функции заданного вида и в виде степенного или обобщенного степенного ряда.
- •25 Лоду второго порядка с ПеремК.
- •26. Способы поиска чр лнду n-го порядка с ПеремК. Неоднородное ду Эйлера.
- •27. Системы обыкновенных ду. Каноническая и нормальная системы. Приведение ду n-го порядка, разрешенного относительно старшей производной, к нормальной сду n-го порядка.
- •28. Сду в нормальной форме. Решение. Общее решение. Частное решение. Задача Коши. Геометрический смысл задачи Коши.
- •29. Сду в нормальной форме. Т. Коши-Пикара. Т. Пеано. Метод Пикара как приближенный метод решения зк.
- •30. Общая теория нормальных cду и ду n-го порядка.
- •31. Лсду в нф. Т. Коши-Пикара. Однородные и неоднородные системы. Некоторые свойства решений однородной системы.
- •32. Лосду в нф. Линейная независимость n частных решений. Определитель Вронского. Формула Остроградского-Лиувилля.
- •33. Лосду в нф. Фср. Теорема об общем решении.
- •34. Задача о построении лосду, имеющей заданную фср.
- •35. Лосду с ПостК. Т. Коши-Пикара. Метод Эйлера построения фср. Случай действительных различных корней характеристического уравнения.
- •36 Лосду с ПостК. Метод Эйлера построения фср. Случай комплексных и кратных корней характеристического уравнения. Теорема об интегрируемости.
- •37. Лнсду. Т. О структуре общего решения. Некоторые свойства решений. Принцип суперпозиции.
- •38. Лнсду. Метод Лагранжа вариации произвольных постоянных для отыскания частного решения. Теорема об интегрируемости.
- •39. Лнсду с ПостК.
- •40. Динамическая интерпретация нормальной соду. Фазовое пространство. Фазовая траектория.
- •41. Автономные и неавтономные динамические системы. Свойства решений автономных динамических систем (адс). Фазовый портрет и бифуркации.
- •42. Виды траекторий адс. Сравнение геометрической интерпретации адс в фазовом и расширенном фазовом пространстве.
- •43. Устойчивость решений динамических систем. Теорема Ляпунова об устойчивости по первому приближению. Критерий Рауса-Гурвица.
- •44. Фазовая плоскость лосду 2 порядка с ПостК. Состояние равновесия типа узел.
- •45. Фазовая плоскость лосду 2 порядка с ПостК. Состояние равновесия типа седло.
- •46. Фазовая плоскость лосду 2 порядка с ПостК. Состояние равновесия типа фокус и центр.
- •47. Фазовая плоскость лосду 2 порядка с ПостК. Состояние равновесия типа вырожденный узел и дикритический узел.
- •48. Исследование устойчивости решений динамических систем с помощью функции Ляпунова.
- •49. Общие методы интегрирования сду. Метод сведения нормальной системы n ду к ду n-го порядка. Метод исключений.
- •50. Теория интегралов нормальных сду. Интеграл. Первый интеграл. НиД условие первого интеграла. Общий интеграл. Решение задачи Коши при наличии общего интеграла.
- •51. Независимость первых интегралов нормальной сду.
- •52. Теоремы о числе первых интегралов нормальной cду и числе независимых первых интегралов.
- •53. Понижение порядка сду с помощью независимых первых интегралов.
- •54. Сду в симметрической форме. Интегрируемые комбинации.
- •55. Лоду в чппп. Характеристическая система.
- •56. Лоду в чппп. Теорема об общем решении.
- •57. Лоду в чппп. Задача Коши.
- •58. Лнду в чппп. Общее решение.
- •59. Лнду в чппп. Задача Коши.
- •60. Лнду в чппп. Обобщённая задача Коши.
8. Линейные ду n-го порядка. Фср. Теорема об общем решении лоду.
- линейное ДУВП.
(1)
ФСР – система n линейно
независимых на
частных решений ЛОДУ n-го
порядка
![]() .
.
Т. о существовании ФСР: уравнение (1) с непрерывными на коэффициентами имеет ФСР на .
Доказательство: выберем
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
…,
,
…,
![]() ,
,
![]() .
Таким образом,
.
Таким образом,
![]() .
.
ФСР с
![]() - нормированная в
.
- нормированная в
.
ЛОДУ имеет бесконечное множество ФСР. При переходе от одной ФСР к другой вронскиан умножается на константу.
Т. об общем решении ЛОДУ (1): пусть
коэффициенты (1) непрерывны на
,
а
- ФСР, тогда
![]() (2)
(2)
Доказательство: при любом наборе
![]() это выражение будет решением. Покажем,
что для любых начальных условий из (2)
можно выделить частное решение.
это выражение будет решением. Покажем,
что для любых начальных условий из (2)
можно выделить частное решение.
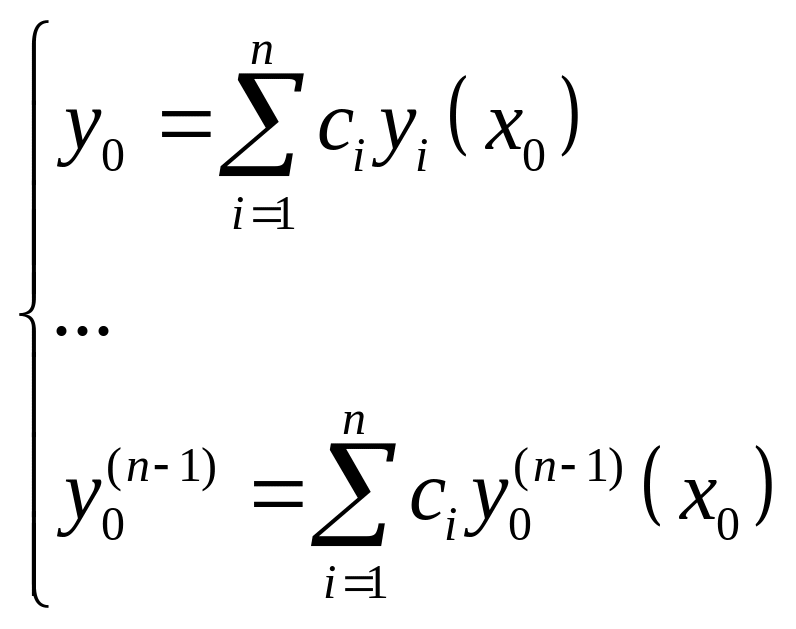 .
Относительно
- линейная однородная алгебраическая
система уравнений с определителем
равным вронскиану, отличному от 0,
следовательно она имеет нетривиальное
решение.
.
Относительно
- линейная однородная алгебраическая
система уравнений с определителем
равным вронскиану, отличному от 0,
следовательно она имеет нетривиальное
решение.
Следствие: максимальное число линейно независимых решений равно порядку уравнения (1).
9. Задача о построении лоду по заданной фср.
Пусть
- система n раз
дифференцируемых, линейно независимых
на
функций и
.
Требуется составить ДУ, для которого
эти функции – ФСР. Т.к. любое решение
искомого уравнения должно быть линейно
зависимым с
,
то
 .
Разложим его по последнему столбцу.
Коэффициент при
.
Разложим его по последнему столбцу.
Коэффициент при
![]() .
Таким образом, это будет уравнение n-го
порядка. При подстановке в него любого
решение в определителе будут 2 одинаковых
столбца, т.е. они будут решениями
уравнения.
.
Таким образом, это будет уравнение n-го
порядка. При подстановке в него любого
решение в определителе будут 2 одинаковых
столбца, т.е. они будут решениями
уравнения.
Т.: пусть даны уравнения
![]() (*) и
(*) и
![]() (**), где
(**), где
![]() непрерывны на
,
имеют одну и ту же ФСР, тогда (*) и (**)
тождественны, т.е.
непрерывны на
,
имеют одну и ту же ФСР, тогда (*) и (**)
тождественны, т.е.
![]() .
.
Доказательство: пусть
![]() .
В силу непрерывности коэффициентов,
они различаются и в некоторой окрестности
.
В этой окрестности
линейно независимы. Вычтем из (*) уравнение
(**), получим
.
В силу непрерывности коэффициентов,
они различаются и в некоторой окрестности
.
В этой окрестности
линейно независимы. Вычтем из (*) уравнение
(**), получим
![]() (***). Пусть
(***). Пусть
![]() - решение (*), следовательно
- решение (*), следовательно
![]() ;
пусть
- решение (**), следовательно
;
пусть
- решение (**), следовательно
![]() .
Таким образом,
.
Таким образом,
![]() ,
следовательно
- решение (***). Таким образом, порядка не
выше
,
следовательно
- решение (***). Таким образом, порядка не
выше
![]() ,
а в окрестности
оно имеет n линейно
независимых решений. Найдено противоречие.
,
а в окрестности
оно имеет n линейно
независимых решений. Найдено противоречие.
Следствие: ФСР однозначно определяет ЛОДУ с непрерывными коэффициентами и старшим коэффициентом равным единице.
10. Лоду n-го порядка с постоянными коэффициентами. Т. Коши-Пикара. Метод Эйлера построения фср. Случай простых корней характеристического уравнения.
![]() - ЛОДУ с постоянными коэффициентами
(1).
- ЛОДУ с постоянными коэффициентами
(1).
Т. Коши-Пикара: для любых конечных начальных условий решение задачи Коши существует и единственно на всей числовой оси.
Метод Эйлера построения ФСР:
При
![]() :
:
![]() ,
,
![]()
При
![]() :
следует искать решение в виде
:
следует искать решение в виде
![]() .
Подставим в (1):
.
Подставим в (1):
![]() ,
,
![]() .
Чтобы уравнение имело решение,
должно быть корнем характеристического
многочлена.
.
Чтобы уравнение имело решение,
должно быть корнем характеристического
многочлена.
1. Если
![]() - простые различные действительные
корни, то каждому
- простые различные действительные
корни, то каждому
![]() .
.
Т.: функции
![]() образуют ФСР на любом
.
образуют ФСР на любом
.
Доказательство:
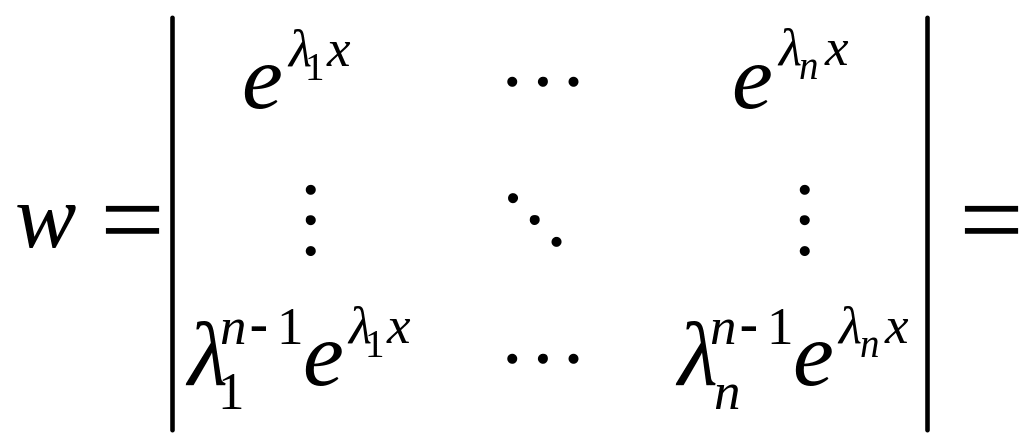
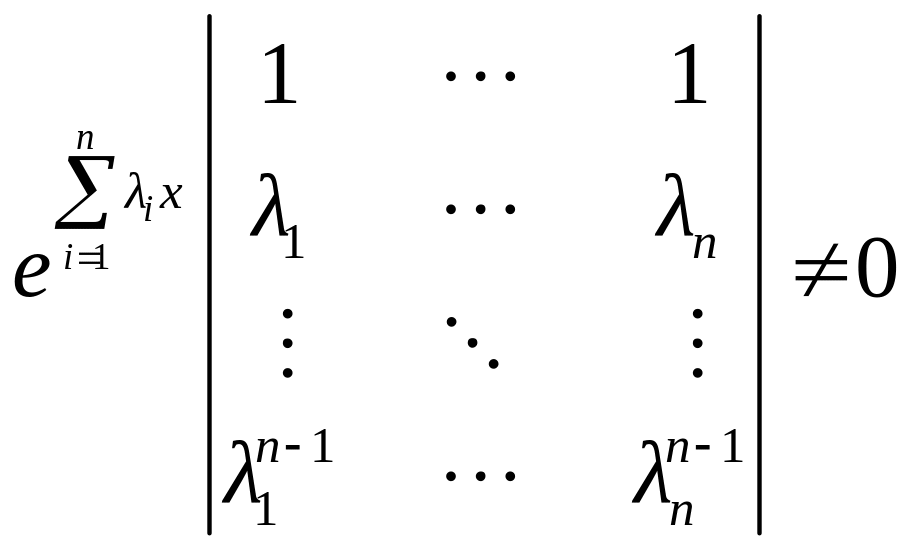
2. Если
различные простые корни, причем,
![]() и
и
![]() .
.
![]() ,
,
![]() .
Решениями являются
.
Решениями являются
![]() ,
,
![]() ,
,
,
,
![]() .
Берут только первые 2 как линейно
независимые.
.
Берут только первые 2 как линейно
независимые.
Т.: функции
,
![]() ,
линейно независима на любом
.
,
линейно независима на любом
.
Доказательство: пусть это не так и эта
система линейно зависима, а
![]() ,
т.е.
,
т.е.
![]() ,
получим
,
получим
![]() .
В итоге получим
.
В итоге получим
![]() .
Разделим на
.
Разделим на
![]() и продифференцируем, повторим. В итоге
и продифференцируем, повторим. В итоге
![]() .
Следовательно,
.
Следовательно,
![]() - обнаружено противоречие.
- обнаружено противоречие.
Т.: функции
,
![]() ,
,
![]() ,
,
образуют ФСР на любом
,
,
образуют ФСР на любом
Доказательство: рассмотрим линейную
комбинацию
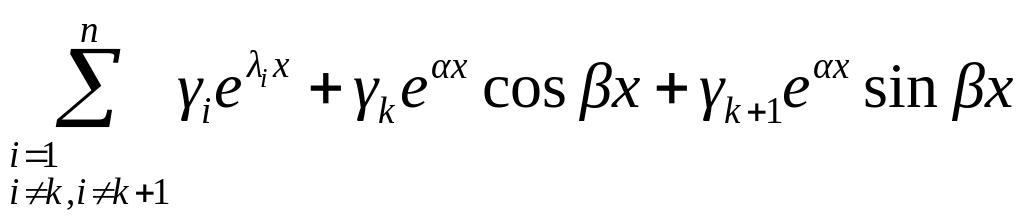 .
Представим
.
Представим
![]()
![]() ,
,
![]()
![]() .
Тогда линейная комбинация примет вид
.
Тогда линейная комбинация примет вид
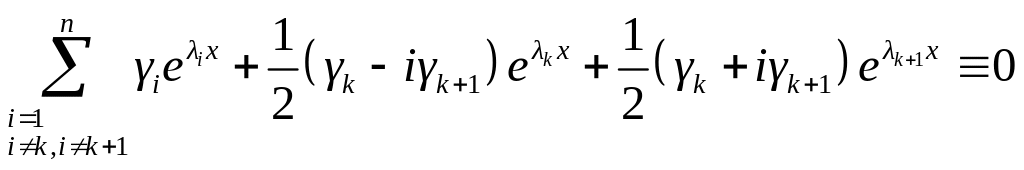 .
По предыдущей теореме, эти функции
линейно независимы только тогда, если
все коэффициенты равны 0, т.е.
.
По предыдущей теореме, эти функции
линейно независимы только тогда, если
все коэффициенты равны 0, т.е.
![]() .
.
