44) Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.

При вычислении интегралов часто бывает удобно сделать замену переменных , где  - непрерывны в некоторой области . Впоследствии мы будем часто писать просто вместо и т.п. и, кроме того, говорить при выполнении вышеупомянутых условий, что и - непрерывно дифференцируемые в функции.

Пусть при этом формулы  задают взаимно-однозначное отображение областей: . Кроме того, не стремясь к минимальности условий, потребуем, чтобы всюду на области

 не равнялся 0.

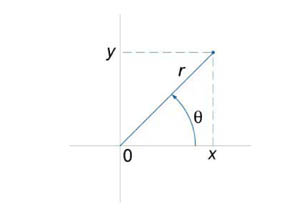
Одним из частных случаев замены переменных является переход из декартовой в полярную систему координат (рисунок 1).

Рис.1		Рис.2

Якобиан такого преобразования имеет вид

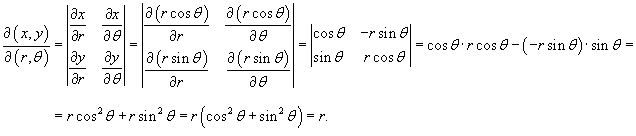
Следовательно, дифференциальный элемент в полярных координатах будет равен

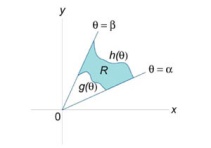
Пусть область интегрирования R в полярных координатах определяется следующим образом (рисунок 2):

Тогда двойной интеграл в полярных координатах описывается формулой

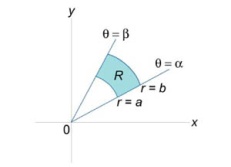
Область интегрирования, показанную на рисунке 3, удовлетворяет условиям

В этом случае формула замены переменных в двойном интеграле имеет вид

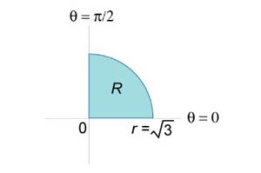
45) Вычисление площади с помощью двойного интеграла

46) Вычисление объемов, ограниченных поверхностями, с помощью двойных интегралов

Пусть тело V ограничено (рис. 2.12)сверху — только одной поверхностью  z = zв(x; y); снизу — только одной поверхностью z = zн(x; y). Линия Lпересечения этих поверхностей проектируется в границу Г области D, на которой заданы непрерывные функции  z = zв(x; y), z = zн(x; y).

При этих условиях:

47) Вычисление массы плоской фигуры (пластины)

Масса плоской пластины вычисляется по ф-ле:

, где (х, у) – поверхностная плотность.

48) Криволинейный интеграл второго рода

Пусть АВ - дуга гладкой кривой (рис. 3.2), на которой определена и непрерывна векторная функция 

Выполним следующие действия:

1) разобьем дугу АВ произвольным образом в направлении от А к B с помощью точек Мi (i = 1, ..., n) на n частичных дуг: Δl1, Δl2, ..., Δli, ..., Δln.

Пусть λn - наибольшая из длин частичных дуг. Понятно, что если λn → 0, то n → ∞  2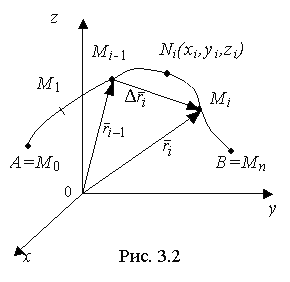 ) выберем произвольным образом точки Ni(xi, yi, zi)   Δli (i=1,...,n)  3) организуем векторы 

и вычислим значения векторной функции   в точках Ni (i = 1, ..., n)  т. е.   (Ni)=(P(Ni), Q(Ni), R(Ni))  4) составим интегральную сумму вида

Определение 3.2 Конечный предел интегральной суммы βn при λn → 0 если он существует и не з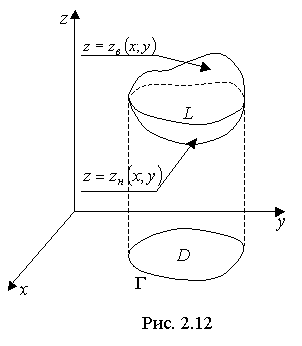 ависит от способа деления дуги АВ на частичные дуги и от способа выбора точек Ni   Δi(i=1,...,n), называется криволинейным интегралом второго рода (по координатам) от векторной функции   =(P,Q,R) по дуге АВ в направлении от А к В и обозначается:

Геометрические и физические приложения интеграла (3.3) разнообразны, некоторые из них будут упомянуты в дальнейшем.

Из построения интеграла (3.3) очевидно, что при изменении направления обхода дуги АВ интеграл меняет знак, т. е.

Об условиях существования интеграла (3.3) говорит следующая теорема.

Теорема 3.2. Если дуга АВ гладкая, и функция   = (P,Q,R) непрерывна на ней, то интеграл (3.3) существует. Можно сформулировать более сильные условия существования криволинейного интеграла по координатам