
- •Первообразная функция. Понятие неопределенного интеграла.
- •8) Интегрирование тригонометрических функций.
- •9) Интегрирование иррациональных уравнений.
- •10) Понятие определенного интеграла.
- •11) Основные свойства определенных интегралов.
- •12) Среднее значение функции.
- •13) Формула Ньютона-Лейбница.
- •14) Замена переменной в определенном интеграле.
- •15)Интегрирование по частям определенного интеграла:
- •16) Вычисление площадей плоских фигур:
- •17)Площадь фигуры в полярных координатах:
- •24)Несобственные интегралы от неограниченных функций.
- •25) Признак сходимости неопределенных интегралов (признак сравнения).
- •26)Определение функции двух переменных. Область определения и область значений функций двух переменных.
- •27) Геометрическое изображение функции двух переменных. Линии уровня.
- •28) Классификация поверхностей второго порядка.
- •36. Касательная плоскость и нормаль к поверхности. Геометрический смысл.
- •42. Основные свойства двойного интеграла.
- •43) Выражение двойного интеграла через повторный.
- •44) Замена переменных в двойном интеграле. Двойной интеграл в полярных координатах.
- •49) Свойства криволинейного интеграла второго рода
10) Понятие определенного интеграла.
Определённый интеграл является площадью части графика функции (в пределах интегрирования), то есть площадью криволинейной трапеции.
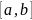 разбиваем
на n
произвольных одинаковых отрезков
длиной
разбиваем
на n
произвольных одинаковых отрезков
длиной
 ,
получаем точки на оси 0x:
,
получаем точки на оси 0x:
 ,
,
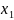 ,
,
 ,
,
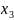 ,
…,
,
…,

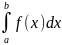

 h+
h+
 h+…
=
h+…
=
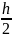 (f(
)+2
(f(
)+2 +
+ +…+2f(
+…+2f( )+2f(
))
=
)+2f(
))
=


11) Основные свойства определенных интегралов.
Теорема 1. Если f(x) и g(x) - две непрерывные функции, заданные на промежутке [a, b], то:
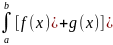 dx
=
dx
=
 ,
,
т. е. интеграл суммы равен сумме интегралов слагаемых.
Теорема 2. Если f(x) - непрерывная функция, а c - постоянное число, то:
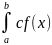 dx=c
,
dx=c
,
т. е. постоянный множитель можно выносить за знак интеграла.
Теорема 3. Пусть f(x) непрерывна на промежутке [a, b]. Если этот промежуток точкой c разложен на части [a, c] и [c, b], то интеграл по всему промежутку оказывается равным сумме интегралов по его частям, т. е.
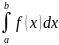 =
= +
+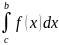 ,
(a<c<b).
,
(a<c<b).
Теорема 4. Если f(x) - неотрицательная непрерывная функция и нижний предел интеграла не больше верхнего, то и сам интеграл будет числом неотрицательным:

12) Среднее значение функции.
Среднее
значение функции — это некоторое число,
заключённое между наименьшим и наибольшим
её значениями. Наиболее важной теоремой
о среднем значении функции в
дифференциальном исчислении является
теорема Лагранжа (теорема о конечном
приращении): если f(x)
непрерывна на отрезке [a,b]
и дифференцируема в интервале (a,b)
, то существует точка “c”,
принадлежащая интервалу (a,b)
, такая, что f(b)
– f(a)
= (b-a) (c).
(c).
В
интегральном исчислении наиболее
важной теоремой о среднем значении
является следующая: если f(x)
непрерывна на отрезке [a,b],
a
 (x)
сохраняет постоянный знак, то существует
точка “c”
из интервала (a,b)
такая, что
(x)
сохраняет постоянный знак, то существует
точка “c”
из интервала (a,b)
такая, что
 = f(c)
= f(c)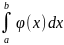
В
частности, если
 =1, то
=1, то
=f(c)(b-a)
Вследствие этого под средним значением функции f(x) на отрезке [a,b] обычно понимают величину:
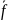 =
=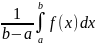
Аналогично определяется среднее значение функции нескольких переменных в некоторой области.
13) Формула Ньютона-Лейбница.
Пусть функция y = f(x) непрерывна на отрезке [a; b] и F(x) - одна из первообразных функции на этом отрезке, тогда справедливо равенство =F(b)-F(a) - основная формула интегрального исчисления.
Благодаря формуле Ньютона-Лейбница устанавливается связь между определенным и неопределенным интегралом. А именно:
Чтобы решить определенный интеграл, надо сначала вычислить неопределенный интеграл (или найти первообразную), а затем вычислить определенный интеграл, подставив первообразную подынтегральной функции в формулу Ньютона-Лейбница.
Пример:
![]()
14) Замена переменной в определенном интеграле.
При вычислении определенных интегралов с использованием формулы Ньютона-Лейбница предпочтительно жестко не разграничивать этапы решения задачи (нахождение первообразной подынтегральной функции, нахождение приращения первообразной). Такой подход, использующий, в частности, формулы замены переменной и интегрирования по частям для определенного интеграла, обычно позволяет упростить запись решения.
ТЕОРЕМА.
Пусть функция φ(t) имеет непрерывную
производную на отрезке [α,β], а=
(α),
в=
(β)
и функция f(х) непрерывна в каждой точке
х вида х=
(t),
где t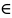 [α,β],
Тогда справедливо следующее равенство:
=
[α,β],
Тогда справедливо следующее равенство:
=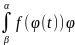 ’(t)dt
’(t)dt
Эта формула носит название формулы замены переменной в определенном интеграле.
Подобно тому, как это было в случае неопределенного интеграла, использование замены переменной позволяет упростить интеграл, приблизив его к табличному (табличным). При этом в отличие от неопределенного интеграла в данном случае нет необходимости возвращаться к исходной переменной интегрирования. Достаточно лишь найти пределы интегрирования α и β по новой переменной t как решение относительно переменной t уравнений φ(t)=а и φ(t)=в. На практике, выполняя замену переменной, часто начинают с того, что указывают выражение t=ψ(х) новой переменной через старую. В этом случае нахождение пределов интегрирования по переменной t упрощается: α=ψ(а), β=ψ(в).
