24. Возрастание и убывание в точке дифференцируемой функции. Теорема Ферма.

Если ф-я f(x) дифференцируема на интервале (a;b) и , то эта ф-я возрастает (убывает) на интервале (a;b).

Исследование ф-ии на возрастание и убывание:

f(x)=x³-6x²-9x+1

1. D(f): (+∞;-∞)

2. f ^I(x)=3x²-12x+9= 3(x-3)(x-1)

f ^I > 0

f ^I < 0 при х прин.(1;3)

Функция убывает на (1;3)

Th. (Ферма). Если f(x) дифф. в точке x₀ и принимает в этой точке наибольш. или наименьш. значение для некоторой окрестности точки x₀, то f ’(x)=0.

Доказательство:

пусть f(x₀) – наибольшая.

25. Теорема Ролля.

Теорема: Если функция f(x) непрерывна на отрезке [a,b], дифференцируемая на отрезке (а,b) и на концах отрезка принимает одинаковое значение f(a)=f(b), то найдется хотя бы одна точка с(а,b), в которой производная f '(х) превращается в ноль, т.е. (f '(с)=0).

Доказательство: Пусть функция f(x) непрерывна на отрезке [a,b], тогда она достигает своего наибольшего значения М и наименьшего значения m на этом отрезке. Рассмотрим случаи:

1) Если М=m, то функция постоянна на [a,b] и следовательно f '(х)=0, (т.к. с'=0); 2) Если Mm, то функция достигает хотя бы одно из значений M или m во внутренних точках с на отрезке (a,b), т.к. f(а)=f(b).

Пусть например: 1) Функция принимает значение М в точке х=с(а,b), т.е. (Рис1) f(с)=M,тогда х(а,b) выполняется соотношение f(c)>=f(x). Найдем производную f '(с) в точке: f '(с)=Lim[f(c+Δx)-f(c)]/Δx, т.к. f(c)>=f(x), то f(c+Δx)-f(c)<=0

• Если Δх>0(т.е. Δх0 справа от точки х=с), то [f(c+Δx)-f(c)]/Δx<=0, поэтому f '(с)<=0

• Если Δх<0, то [f(c+Δx)-f(c)]/Δx>=0, то f '(с)>=0. Таким образом, получим, что f '(c)<=0 и f ’(с)>=0| f '(с)=0

2) Если f(с)=m, доказательство аналогично.

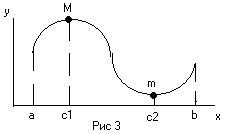
Примечание: Геометрически Теорема Ролля означает, что на графике функции y=f(x) найдется точка в которой касательная к графику параллельна оси ох (см. Рис1 и Рис2), (на Рис3 таких точек 2-е).

26. Формула Лагранжа и следствия из нее.

Если f(x) непрерывна на [a;b], дифференцируема на (a;b), то найдется хотя бы одна точка , такая, чтоf(b)-f(a)=f ^I(c)(b-a)

ДОКАЗАТЕЛЬСТВО:

Положим в т. Коши φ(x)=x

Подставим эти значения в формулу:

Что и требовалось доказать.

Геометрический смысл т. Лагранжа:

Отношение f(b)-f(a) / b-a есть угловой коэффициент секущей АВ, а величина f ^I(c) – угловой коэффициент касательной к кривой в точке x=c, следовательно геометрический смысл т. Лагранжа заключается в следующем: на графике y=f(x) найдется точка C(c;f(c)) в которой касательная к графику функции параллельна секущей АВ.

СЛЕДСТВИЕ:Если, производная функции yⁱ=0 на некотором промежутке, то ф-я постоянна на этом промежутке.

Если две ф-ии имеют равные производные на некотором промежутке, то они отличны друг друга на постоянное слагаемое.

27. Формула Коши.

Если f(x), g(x) удовл. трем условиям:

1). f(x), g(x) непрерыв. на промеж [a,b]

2). f(x), g(x) диффер. на интервале (a,b)

3). g’(x)0 на интер. (a,b), то сущ. т. с

g(b)g(a) (неравны по теореме Ролля).

1). F(x) – непрерывна на [a,b]

2). F(x) – дефференцированна на (a,b)

3). F(a)=0 ; F(b)=0

по теореме Ролля сущ. с(a,b); f ’(с)=0