
- •1.Компоненты перемещений и деформаций в элементарном объеме
- •2.Тензор деформаций
- •3. Неразрывная деформация
- •4.Скорость перемещения, скорость деформации
- •6. Условие пластичности.
- •7. Физический смысл условия пластичности.
- •8.Геометрический смысл условия пластичности.
- •9. Частные случаи выражения пластичности.
- •1 0.Влияние среднего по величине главного напряжения.
- •11.Связь между напряжениями деформации при пластическом деформировании.
- •16. Особенности пластического трения
- •17. Факторы,влияющие на величину сил контактного трения. Законы трения
- •39. Прокатка. Основные положения
- •21.Основы метода расчета усилий деформирования по приближенным уравнениям равновесия и условию пластичности
- •22.Метод линий скольжения
- •25. Метод сопротивления материалов пластической деф-и (метод Смирного-Алеева)
- •26. Метод баланса работ.
- •44 Инварианты тензора напряжений
1.Компоненты перемещений и деформаций в элементарном объеме
При обработке давлением металл получает остаточные значительные деформации. Если тело деформируется, то каждая точка смещается из своего первоначального положения, однако тело находится в равновесии и не имеет возможности перемещаться на 1 целое. Перемещение точки при пластической деформации происходит исключительно в следствии деформации.
Если координатная точка в начальный момент соответственно равно x,y,z, а после деформации x',y',z', то параметры
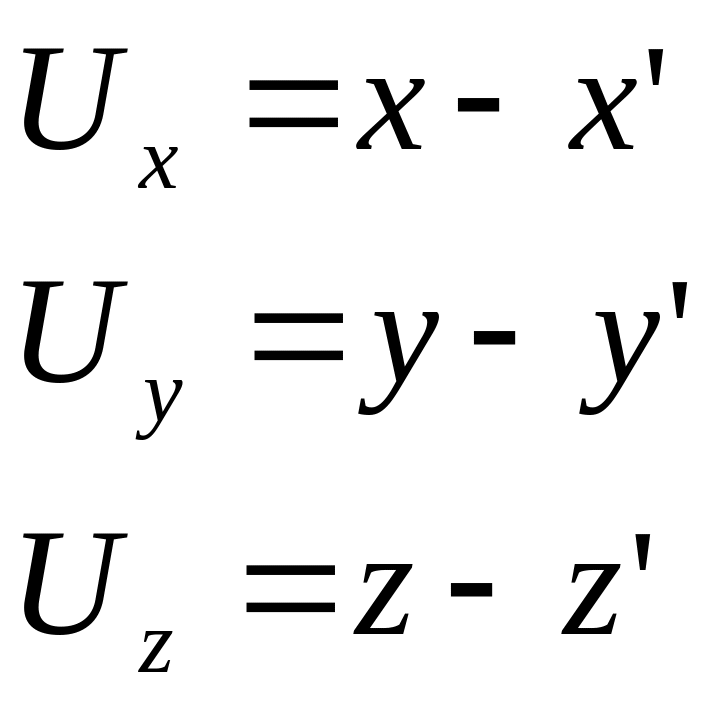
Проекции перемещений на характерные оси – компоненты перемещений точки. Компоненты перемещений точек тела и их производные являются непрерывной функции координат.
В общем случае
элементарный прямоугольный параллелепипед
после деформации изменит не только свое
положение, но и форму. Длина ребер
изменяется, а углы перестанут быть
прямыми. В приделах малых деформаций
будут иметь место наличие 2 видов
деформаций: линейные относительные
величина которых равна
![]() и угловых или сдвиговых
и угловых или сдвиговых
![]()
![]()
![]()
В процессе деформации при проектировании на соответствующие оси
![]()
В процессе деформации
происходит поворот соответственных
ребер ab в направлении оси y на <![]() а ребра ac на <
а ребра ac на <![]() в направлении оси x причем суммарная
сдвиговая деформация
в направлении оси x причем суммарная
сдвиговая деформация
![]()
Выразим компоненты
деформации через компоненты перемещений
точек элементарного параллелепипеда.
Для этого выделим в окрестностях точки
M деформированного тела с малыми ребрами
![]() а его вершина совпадает с т A
а его вершина совпадает с т A
abcd – проекция элементарного параллелепипеда на плоскость xy до деформации.
т. a совпадает с т. М После деформации данного параметра т. abcd полочим перемещение
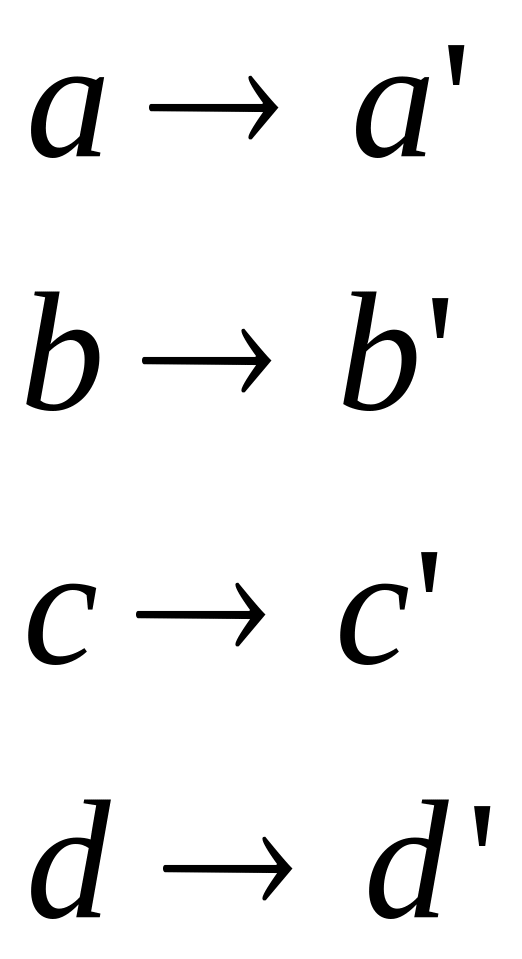
в результате имеем (см рис)
В результате
деформации перемещения т. a в направлении
оси x это
![]() ,
а в направлении оси y -
,
а в направлении оси y -![]()
![]()
Точка b находится
на бесконечно малом расстоянии
![]() от т.а в направлении оси х. перемещение
т.
от т.а в направлении оси х. перемещение
т.![]() будет отличаться от перемещения т.а на
бесконечно малое приращение
будет отличаться от перемещения т.а на
бесконечно малое приращение
![]()
Аналогично перемещение т.с в направлении оси у будет отличаться от перемещения т.а в направлении оси у на бесконечно малую величину
![]()
![]()
![]()
Аналогично можно
получить
![]()
Перемещение точки
![]() будет
отличаться от перемещения точки
на
бесконечно малую величину:
будет
отличаться от перемещения точки
на
бесконечно малую величину:
![]()
Аналогично
определяется перемещение точки
![]()
![]()
С![]() читается,
что тангенсы угла поворота
и
для малых деформаций равны соответствующим
углам. Их треугольника
читается,
что тангенсы угла поворота
и
для малых деформаций равны соответствующим
углам. Их треугольника
![]() при малости угла
при малости угла
![]()
Для малых деформаций
величина![]() является малой величиной < 1, т.о.
является малой величиной < 1, т.о.
![]()
Аналогично из
треугольника
![]() можно
получить
можно
получить
![]() ;
;
![]()
Результирующая сдвиговая деформация определяется как сумма послкдних
![]()
Поступая аналогичным образом можно определить все выражения характеризующие линейные и сдвиговые деформации:
![]() ;
;![]() ;
;
;
;
![]() ;
;![]() ;
;![]()
Данные уравнения носят названия уравнения Каши
Величина пластических
сдвигов
![]() является
суммой углов поворота ребер элементарного
параллелепипеда в направлении
соответствующей оси. Результат изменения
формы безразличен в отношении угла
альфа, лишь бы их сумма оставалась
постоянной и равной
является
суммой углов поворота ребер элементарного
параллелепипеда в направлении
соответствующей оси. Результат изменения
формы безразличен в отношении угла
альфа, лишь бы их сумма оставалась
постоянной и равной
![]() .
Это дает возможность представлять
данные сдвиговых деформаций равными
между собой и воспользоваться записью
тензора напряжений, т.о. деформируемое
состояние характеризуется некоторым
тензором
.
Это дает возможность представлять
данные сдвиговых деформаций равными
между собой и воспользоваться записью
тензора напряжений, т.о. деформируемое
состояние характеризуется некоторым
тензором
![]() :
:
![]()
По аналогии с напряженным состоянием тензор деформации может быть разложен на 2 составляющие:
![]() ,
,
где
![]() - шаровой тензор деформаций;
- шаровой тензор деформаций;
![]() - девиатор деформаций;
- девиатор деформаций;
Из условия постоянства
объема:
![]()
