1. Певообразная и ее свойства

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x), что выполняется равенство для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство . Таким образом, функция f(x) имеет множество первообразных F(x)+C, для произвольной константы С, причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Свойства первообразной.

Если функция F(x) - первообразная для функции f(x) на интервале X, то функция f(x) + C, где C - произвольная постоянная, тоже будет первообразной для f(x) на этом интервале.

Если функция F(x) - некоторая первообразная для функции f(x) на интервале X=(a,b), то любая другая первообразная F1(x) может быть представлена в виде F1(x) = F(x) + C, где C - постоянная на X функция.

2 Определение неопределенного интеграла.

Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .

Выражение называют подынтегральным выражением, а f(x) – подынтегральной функцией. Подынтегральное выражение представляет собой дифференциал функции f(x).

Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x), а множество ее первообразных F(x)+C.

свойства неопределенного интеграла (свойства первообразной).

Производная результата интегрирования равна подынтегральной функции.

Неопределенный интеграл дифференциала функции равен сумме самой функции и произвольной константы.

где k – произвольная константа. Коэффициент можно выносить за знак неопределенного интеграла.

Неопределенный интеграл суммы/разности функций равен сумме/разности неопределенных интегралов функций.

3. Замена переменной в неопределенном интеграле

Замена переменной в неопределенном интеграле производится с помощью подстановок двух видов:

а) где монотонная, непрерывно дифференцируемая функция новой переменной t. Формула замены переменной в этом случае:

где U – новая переменная. Формула замены переменной при такой подстановке:

Интегрирование по частям

Нахождение интеграла по формуле азывается интегрированием по частям. Здесь U=U(х),υ=υ( x) непрерывно дифференцируемые функции от х. С помощью этой формулы нахождение интеграла сводится к отысканию другого интеграла ее применение целесообразно в тех случаях, когда последний интеграл либо проще исходного, либо ему подобен.

При этом за υ берется такая функция, которая при дифференцировании упрощается, а за dU – та часть подынтегрального выражения, интеграл от которой известен или может быть найден.

4 Интергрирование рациональных функций

Для интегрирования рациональной функции где P(x) и Q(x) - полиномы, используется следующая последовательность шагов:

Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;

Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;

Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;

Вычислить интегралы от простейших дробей.

5.

. Тогда заданная криволинейная трапеция разобьется на n частей — на n узеньких столбиков. Площадь всей трапеции равна сумме площадей столбиков.

Рассмотрим отдельно k-тый столбик, т.е. криволинейную трапецию, основанием которой служит отрезок Заменим его прямоугольником с тем же основанием и высотой, равной f(хк) (рис. 154). Площадь прямоугольника равна — длина отрезка ; естественно считать составленное произведение приближенным значением площади к-то столбика. сли теперь сделать то же самое со всеми остальными столбиками, то придем к следующему результату: площадь 5 заданной криволинейной трапеции приближенно равна площади 5. ступенчатой фигуры, составленной из п прямоугольников (рис. 155). Имеем: десь ради единообразия обозначений мы считаем, что Итак, S = Sn, причем это приближенное равенство тем точнее, чем больше п.

Принято считать, что искомая площадь есть предел последовательности s=limS

Определение определённого интеграла

Если существует конечный предел I интегральной суммы при λ → 0, и он не зависит от способа выбора точек ξ i, способа разбиения отрезка, то этот предел называется определенным интегралом от функции f (x)по отрезку [a, b] и обозначается следующим образом:

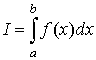
Или В этом случае функция f (x) называется интегрируемой на [a, b]. Числа a и b называются соответственно нижним и верхним пределами интегрирования, f (x) – подынтегральной функцией, х – переменной интегрирования.

Свойства определённых интегралов

Определённый интеграл численно равен площади криволинейной трапеции, ограниченной графиком функции у = f (x), осью абсцисс, и прямыми х = а, х = b.

Если нижний и верхний пределы интегрирования поменять местами, то значение определённого интеграла изменится на противоположное

Если промежуток интегрирования стянут в точку, фигура под кривой стягивается в отрезок, площадь которого равна нулю

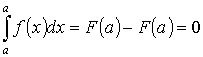
Постоянный множитель можно выносить за знак интеграла

Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:

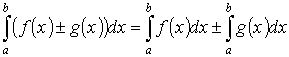
Если промежуток интегрирования разбит на части, то интеграл по всему отрезку равен сумме интегралов по каждой части.

Если на отрезке [a, b], где а < b, имеет место неравенство 0 ≤ f (x) ≤ g (x), то

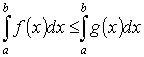
Если функция y = f (x) непрерывна на отрезке [a, b], где а < b, то найдется такое значение c Î [a, b], что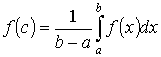

7.

Формула Ньютона–Лейбница

Непрерывность определенного интеграла как функции верхнего предела

Если функция y = f (x) интегрируема на отрезке [a, b], то, очевидно, она интегрируема также на произвольном отрезке [а, х], вложенном в [a, b]. Функция ,

где х Î [a, b], называется интегралом с переменным верхним пределом. Значение функции Ф (х) в точке х равно площади S(x) под кривой y = f (x) на отрезке [а, х]. В этом состоит геометрический смысл интеграла с переменным верхним пределом.

Теорема. Если функция f (x) непрерывна на отрезке [a, b] то функция Ф (х) также непрерывна на [а, b].

Пусть Δх таково, что х + Δ х Î [a, b]. Имеем

По теореме о среднем найдется такое значение с Î [ x, x + Δ x], что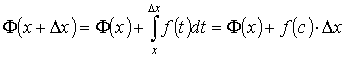 Поскольку с Î [x, x + Δ x], и функция f (x) ограничена, то переходя к пределу при Δ x → 0, получим