
Математические основы моделирования сложных физических систем
.pdfВ. А. Смоляр, И. И. Маглеванный, А. С. Ситников
Математические основы моделирования сложных физических систем

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВОЛГОГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
В. А. Смоляр, И. И. Маглеванный, А. С. Ситников
МАТЕМАТИЧЕСКИЕ ОСНОВЫ
МОДЕЛИРОВАНИЯ СЛОЖНЫХ
ФИЗИЧЕСКИХ СИСТЕМ
Учебное пособие
Волгоград
2010
УДК 548
Р е ц е н з е н т ы :
зав. кафедрой "Общая физика" ВолгГАСУ д-р физ.-мат. наук, профессор А. И. Бурханов;
зав. кафедрой "Высшая математика" ВолгГАСУ д-р физ.-мат. наук, профессор И. П. Руденок
Издается по решению редакционно-издательского совета Волгоградского государственного технического университета
Смоляр, В. А.
Математические основы моделирования сложных физических систем : учеб. пособие / В. А. Смоляр, И. И. Маглеванный, А. С. Ситников. – Волгоград : ИУНЛ ВолгГТУ, 2010. – 80с.
ISBN 978–5–9948–0576–3
Изложены основы метода конечных элементов на примере реальных физических задач, начиная с простой дискретной задачи о нагруженном составном стержне и заканчивая решением задачи, описываемой волновым уравнением с затуханием.
Предназначено для студентов старших курсов физических специальностей технических университетов.
.
Ил. 5. Библиогр.: 6 назв.
ISBN 978–5–9948–0576–3 |
© Волгоградский государственный |
|
технический университет, 2010 |
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ |
5 |
|
1. ОСНОВЫ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ |
6 |
|
|
1.1. Дискретная задача – первое знакомство с методом конечных |
6 |
|
элементов |
|
|
|
|
|
1.2. Континуальные задачи |
17 |
|
1.3. Метод Галеркина |
20 |
|
1.4. Пример вычислительной программы |
27 |
2. |
НЕОДНОРОДНЫЙ НАГРУЖЕННЫЙ СТЕРЖЕНЬ |
28 |
|
2.1. Переход к интегральной форме |
28 |
|
2.2. Кусочно-линейные пробные функции |
29 |
|
2.3. Контрольный пример |
31 |
|
2.4. Нормированные пробные функции |
34 |
|
2.5. Матричные коэффициенты |
36 |
|
2.6. Пример вычислительной программы |
38 |
3. |
СТАЦИОНАРНАЯ ДИФФУЗИЯ-КОНВЕКЦИЯ |
39 |
|
3.1. Дискретизация задачи |
39 |
|
3.2. Получение слабой формы |
40 |
|
3.3. Матричные коэффициенты на сетке узлов с изменяющимся шагом |
41 |
|
3.4. Пример вычислительной программы |
47 |
4. ДИФФУЗИЯ ЭЛЕКТРОНОВ В МНОГОСЛОЙНОЙ СТРУКТУРЕ |
48 |
|
|
4.1. Классическая и обобщенная постановка задачи |
48 |
|
4.2. Пространственная дискретизация обобщенной задачи Коши |
51 |
|
4.3. Обобщенные уравнения баланса |
58 |
3
4.4. Разностная аппроксимация |
59 |
4.5. Расщепление эволюционной задачи Коши |
65 |
4.6. Пример вычислительной программы |
68 |
5. ВОЛНОВОЕ УРАВНЕНИЕ С ЗАТУХАНИЕМ |
69 |
5.1. Классическая постановка начально-краевой задачи |
69 |
5.2. Обобщенная постановка задачи |
70 |
5.3. Пространственная дискретизация обобщенной задачи Коши |
70 |
5.4. Обобщенное уравнение баланса |
73 |
5.5. Разностная аппроксимация |
73 |
5.6. Решение эволюционной задачи |
75 |
5.7. Пример вычислительной программы |
76 |
ЗАКЛЮЧЕНИЕ |
77 |
СПИСОК ЛИТЕРАТУРЫ |
79 |
|
4
ВВЕДЕНИЕ В науке и технике постоянно приходится иметь дело с проблемой
расчета сложных физических систем. Компьютеры позволяют выполнять такие расчеты при помощи приближенных численных методов. Метод конечных элементов (МКЭ), в специальной литературе называемый также методом обобщенных решений, является одним из них. В последние десятилетия он получил широкое применение и реализован в пакетах вычислительных программ, ориентированных на применение в различных областях физики.
Метод конечных элементов применяется в решателях уравнений в частных производных второго порядка в больших универсальных компьютерных пакетах программ, например, MATLAB, FEMLAB. Это коммерческое программное обеспечение. В больших универсальных компьютерных пакетах программ со свободным доступом - SCILAB, OCTAVE - используются накопленные в течение десятилетий библиотеки научных математических программ со свободным доступом - GSL (Gnu
Sientific Lybrary), например. В этих библиотеках и построенных на их основе универсальных математических пакетах имеются решатели систем обыкновенных дифференциальных уравнений, но пока нет программ -
решателей уравнений в частных производных с граничными условиями. По этой причине для задачи, приводящей к уравнению в частных производных,
приходится создавать свой решатель.
Естественными инструментом программирования, если вы не хотите пользоваться коммерческими пакетами программ, является свободное программное обеспечение - компилятор GСС (Gnu Compiler Collection) с
дебагером GDB для изучения и отладки программ в среде LINUX.
Приведенные в Приложении на CD программы выполнены именно по этой
5
технологии, они отвечают требованиям лицензии GPL - 3 (Gnu Public Licens)
и могут свободно копироваться, распространяться и изменяться с любыми, в
том числе и с коммерческими целями, хотя главная задача авторов - это применение в учебном процессе для обучения студентов технических и физических специальностей не только практическому применению метода конечных элементов, но и пониманию проблемы расширения классического понятия решения дифференциального уравнения и выработки понятия обобщенного решения.
В данном учебном пособии на простых примерах мы рассмотрим сущность метода конечных элементов и шаг за шагом, переходя от простого к сложному, покажем как реализовать эту сущность в вычислительных программах-решателях эллиптических, параболических и гиперболических уравнений. Мы доводим изложение метода до числа на одномерных задачах о механических деформациях стержня, диффузии электронов и распространии сильно затухающей волны, подробно описываем каждый шаг аналитических вычислений и приводим тексты программ, реализующих вычислительные алгоритмы на прилагаемом CD.
1.ОСНОВЫ МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ
1.1.Дискретная задача - первое знакомство с методом конечных
элементов Знакомство с методом конечных элементов начнем с простой
дискретной задачи, состояние которой точно определяется конечным числом параметров. Рассмотрим упругий стержень в виде прямого кругового цилиндра, длина которого значительно больше его диаметра. Стержень составлен из отделльных соединенных в узлах элементов различной жесткости и нагружен в узлах внешними силами вдоль его оси (рисунок 1.1).
6
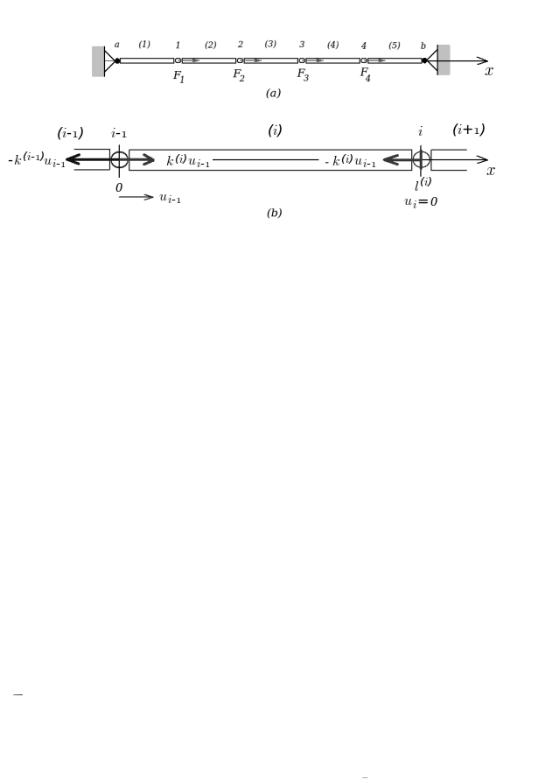
Точки a и b закреплены, что условно изображено на рисунке.
Рисунок 1.1 - Пример дискретной задачи
Пусть ось x с началом координат в точке a направлена вдоль стержня.
Очевидно, точки на осях стержней перемещаются вдоль x . Силы и
перемещения считаются положительными, если они направлены в положительном направлении x . Задача состоит в определении перемещений точек, принадлежащих осям стержней и продольных внутренних сил в поперечных сечениях стержней.
Согласно методу конечных элементов, представим стержневую систему в виде элементов, соединенных в узлах. В качестве элементов примем отдельные стержни, а узлов - точки их соединения. На рисунке 1.1 в скобках
указаны номера элементов, а без скобок - номера узлов.
Обратимся к типовому для данной системы элементу (i) . На элемент с
узлами i 1,i (рисунок 1.1) может действовать распределенная нагрузка
интенсивности q(i ) (x) . Размерность интенсивности нагрузки - сила/(единица
длины). Обозначим перемещения узлов элемента ui(i1) , ui(i) . Обозначим длину
элемента l(i) . Получим задачу для функции перемещений точек оси x .
7

Бесконечно малая часть элемента находится в равновесии под действием нагрузки и продольных внутренних упругих сил f (i) (x)
|
(i) |
|
(i) du(i) |
(1.1) |
||
f |
|
(x) = c |
|
|
, |
|
|
|
|||||
|
|
|
|
dx |
|
|
где c(i) > 0 носит название продольной жесткости стержня и определяется из
опыта.
Стержень будет находится в равновесии при равенстве упругих внутренних и приложенных внешних сил в каждом его элементе dx :
|
df (i) |
|
|
df (i) q(i)dx = 0, |
|
= q(i) , |
(1.2) |
|
|||
|
dx |
|
|
Пусть c(i) = const для элемента i . Подставляя (1.1) в (1.2) |
получим задачу |
||
относительно u(i ) (x) в виде дифференциального уравнения и граничных условий:
c |
(i) d 2u(i) |
= q |
(i) |
, |
|
(1.3) |
||
|
d 2 x |
|
|
|||||
|
|
|
|
|
|
|
||
u(i) (x |
) = u |
, u(i) (x ) = u . |
|
|||||
i 1 |
|
i 1 |
|
|
|
i |
i |
|
В нашем примере для случая дискретной задачи положим |
q(i ) = 0 и будем |
|||||||
считать, что на стержневую систему |
действуют только |
внешние силы |
||||||
сосредоточенные в узлах Fi . Внешняя нагрузка уравновешивается силами упругости стержней fi = Fi , и система находится в равновесии, получив в каждом узле некоторое смещение ui . Тогда решение уравнения (1.3) примет вид:
u(i) (x) = |
ui(i) ui(i |
1) |
x |
u(i) , |
(1.4) |
l(i) |
|
||||
|
|
|
i 1 |
|
|
На основании (1.4) можно заключить, что состояние типового элемента |
|||||
i , то есть u(i) (x), f (i) (x) , точно определяется двумя |
параметрами - |
||||
8 |
|
|
|
|
|

перемещениями его узлов u(i) ,u(i) . Действительно, подставив решение (1.4), в |
|||||||
i |
j |
|
|
|
|
|
|
(1.1), получим |
|
|
|
|
|
|
|
f (i) (x) = |
(i) u(i) |
u(i) |
, |
(i) = |
c(i) |
. |
(1.5) |
|
|||||||
|
i |
i 1 |
|
|
l(i) |
|
|
Это делает задачу нахождения связи между перемещениями узлов
составного стрежня и силами в узлах линейной.
Рассмотрим внутренние упругие силы fi (i ) действующие в узле i на элемент (i) . Поскольку имеет место линейная задача, то они линейно зависят
от u(i ) |
, u(i) : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i 1 |
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (i) = |
f (i)u(i) |
f (i) u(i) , |
|
|
|
|||||||||
|
|
|
|
|
|
i |
|
|
|
|
ii |
|
|
i |
i,i 1 |
i 1 |
|
|
(1.6) |
|
|
|
|
|
|
|
f (i) = f (i) |
u(i) |
f (i) |
u(i) . |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
i 1 |
|
i 1,i |
|
i |
i 1,i 1 i 1 |
|
|
|
||||||
Здесь |
f (i) , l = i,i |
1; |
t = i,i |
1 |
есть внутренняя |
сила, |
действующая на |
|||||||||||||
|
|
lt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
элемент i в узле l |
и возникающая от единичного перемещения узла t . При |
|||||||||||||||||||
этом перемещение другого узла равно нулю. |
|
|
|
|
||||||||||||||||
|
Воспользовавшись уравнением (1.5), получим |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
f (i) = |
|
(i)u(i) |
(i)u(i) , |
|
|
(1.7) |
|||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
i |
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
f |
(i) = |
(i)u(i) |
(i)u(i) . |
|
|
|
|||||||
|
|
|
|
|
|
|
|
i |
1 |
|
|
i |
|
|
i |
1 |
|
|
|
|
|
Соотношения (1.5) можно представить в матричной форме. Введем |
|||||||||||||||||||
столбцы f(i ) , u(i ) и матрицу K(i ) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
f (i) |
|
f |
(i) |
|
, u(i) |
|
u(i) |
|
, K (i) = |
|
(i) |
(i) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
i |
|
|
|
i |
|
|
|
|
|
. |
(1.8) |
|||||
|
|
|
|
|
f |
(i) |
|
|
|
|
u(i) |
|
|
|
|
(i) |
(i) |
|
|
|
|
|
|
|
|
i |
1 |
|
|
|
|
i |
1 |
|
|
|
|
|
|
|
|
Тогда (1.5) можно записать в виде: |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
f (i) = K (i)u(i) . |
|
|
|
(1.9) |
|||||||
Для упругой пружины коэффициент пропорциональности между силой и перемещением называется коэффициентом жесткости пружины. Аналогично
9
