
- •Вопрос 1
- •Вопрос 2
- •Вопрос 3
- •Вопрос 4
- •Вопрос 5
- •Вопрос 6
- •Вопрос 7
- •Вопрос 8
- •Вопрос 9 Соотношение неопределённостей Гейзенберга
- •Вопрос 10 .Волновая функция и ее статистический смысл
- •Вопрос 11 Стационарное уравнение Шрёдингера
- •Вопрос 12
- •Вопрос 14 Прохождение частицы сквозь потенциальный барьер, туннельный эффект
- •Вопрос 15 Квантовый гармонический осциллятор
- •Вопрос 16 Решение уравнения Шрёдингера
- •Вопрос 17 Квантование энергии электрона в атоме
- •Линейчатый спектр атома водорода
- •1. Орбитальный механический момент импульса электрона
- •Вопрос 19
- •Вопрос 20
- •Структура периодической системы
- •Значение периодической системы
- •Вопрос 21 Поглощение, спонтанное и вынужденное излучения
- •Эйнштейна коэффициенты
- •Вопрос 22
- •Принцип действия лазера
- •Вопрос 23
- •1. Классическая теория теплоёмкости. Модель независимых осцилляторов
- •Вопрос 26
- •Вопрос 27
- •Вопрос 28
- •§ 77. Периодическая система элементов Менделеева
- •Вопрос 29
- •Вопрос 30
- •13.Температурная зависимость электропроводимости п/п-ов.
- •Вопрос 32
- •Масса и энергия связи ядра
- •Вопрос 33
- •Гамма-лучи
- •Бета-лучи
- •Альфа-частицы
- •Законы сохранения в ядерных реакциях
- •Закон сохранения энергии
- •Закон сохранения импульса
- •Закон сохранения момента импульса
- •Другие законы сохранения
- •Вопрос 35
- •Вопрос 36
Вопрос 23
С помощью этой формулы Планка мы можем получить все ответы на вопросы, связанные с твёрдым телом.
1. Классическая теория теплоёмкости. Модель независимых осцилляторов
Т вёрдое
тело может быть смоделировано частицами,
которые колеблются относительно
положения равновесия. Частицы в узлах
решётки сидят и при нагревании колеблются,
поэтому простейшая модель такая: частица
массы m
привязана пружинкой жёсткости k
к положению равновесия. На самом деле,
там пусто и привязаться не к чему, мы
делаем модель. Каждый атом с положением
равновесия в узлах решётки мы моделируем
независимым осциллятором. Энергия
осциллятора
вёрдое
тело может быть смоделировано частицами,
которые колеблются относительно
положения равновесия. Частицы в узлах
решётки сидят и при нагревании колеблются,
поэтому простейшая модель такая: частица
массы m
привязана пружинкой жёсткости k
к положению равновесия. На самом деле,
там пусто и привязаться не к чему, мы
делаем модель. Каждый атом с положением
равновесия в узлах решётки мы моделируем
независимым осциллятором. Энергия
осциллятора
![]() .
Можно доказать, что средняя кинетическая
энергия осциллятора равна средней
потенциальной энергии:
.
Можно доказать, что средняя кинетическая
энергия осциллятора равна средней
потенциальной энергии:
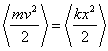 .
Из статистической физики известно, что
.
Из статистической физики известно, что
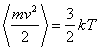 ,
поэтому средняя энергия одного
осциллятора равна
,
поэтому средняя энергия одного
осциллятора равна
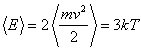 .
Тогда внутренняя энергия одного моля
будет равняться
.
Тогда внутренняя энергия одного моля
будет равняться
![]() ,
а теплоёмкость
,
а теплоёмкость
![]()
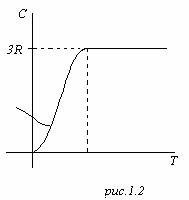
![]() Классическая
теория говорит, что теплоёмкость одного
моля любого твёрдого тела равна 3R.
На самом деле, теплопроводность твёрдых
тел экспериментально имеет такой вид
(рис.1.2).
Классическая
теория говорит, что теплоёмкость одного
моля любого твёрдого тела равна 3R.
На самом деле, теплопроводность твёрдых
тел экспериментально имеет такой вид
(рис.1.2).
![]()
Элементы современной физики атомов и молекул Атом водорода в квантовой механике
При достаточно низких температурах теплоёмкость падает как T3. Классическая теория не справляется с этим делом.
Энергия
осциллятора квантуется.
![]() ,
,
![]() где
– частота осциллятора. Если учесть
квантование энергии, то средняя энергия,
приходящаяся на одну степень свободы
равна
где
– частота осциллятора. Если учесть
квантование энергии, то средняя энергия,
приходящаяся на одну степень свободы
равна
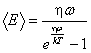 ,
а для пространственного осциллятора
,
а для пространственного осциллятора
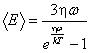
Как
это согласуется с классическим
результатом? Очень просто – при
![]()
![]() и
и
![]() при
при
![]() .
Это уже даёт правильное приближение,
но закон T3
не получается всё равно. Это говорит о
том, что модель независимых осцилляторов
слишком груба.
.
Это уже даёт правильное приближение,
но закон T3
не получается всё равно. Это говорит о
том, что модель независимых осцилляторов
слишком груба.
Закон Дюлонга-Пти (Закон постоянства теплоёмкости) — эмпирический закон, согласно которому молярная теплоёмкость твёрдых тел при комнатной температуре близка к 3R:
![]()
где R — универсальная газовая постоянная.
Закон выводится в предположении, что кристаллическая решетка тела состоит из атомов, каждый из которых совершает гармонические колебания в трех направлениях, определяемыми структурой решетки, причем колебания по различным направлениям абсолютно независимы друг от друга. При этом получается, что каждый атом представляет три осциллятора с энергией E, определяемой следующей формулой:
![]() .
.
Формула
вытекает из теоремы о равнораспределении
энергии
по степеням свободы. Так как каждый
осциллятор имеет одну степень
свободы,
то его средняя кинетическая
энергия
равна
![]() ,
а так как колебания происходят
гармонически, то средняя потенциальная
энергия
равна средней кинетической, а полная
энергия - соответственно их сумме. Число
осцилляторов в одном моле вещества
составляет
,
а так как колебания происходят
гармонически, то средняя потенциальная
энергия
равна средней кинетической, а полная
энергия - соответственно их сумме. Число
осцилляторов в одном моле вещества
составляет
![]() ,
их суммарная энергия численно равна
теплоемкости тела - отсюда и вытекает
закон Дюлонга-Пти.
,
их суммарная энергия численно равна
теплоемкости тела - отсюда и вытекает
закон Дюлонга-Пти.
Приведем таблицу экспериментальных значений теплоемкости ряда химических элементов для нормальных температур:
Элемент |
|
Элемент |
, кал/(К·моль) |
C |
1,44 |
Pt |
6,11 |
B |
2,44 |
Au |
5,99 |
Al |
5,51 |
Pb |
5,94 |
Ca |
5,60 |
U |
6,47 |
Ag |
6,11 |
- |
- |
Зависимость теплоёмкости от температуры при низких температурах объясняется в моделях Эйнштейна и Дебая.
Закон Дебая утверждает, что при низких температурах теплоёмкость твёрдого тела возрастает пропорционально кубу температуры.
Закон Дебая справедлив для диэлектриков и полупроводников при температурах, намного меньших температуры Дебая, которая является характеристикой каждого конкретного вещества. Зная температуру Дебая, теплоёмкость при постоянном объёме можно оценить по формуле
![]() ,
,
где
N — число атомов,
![]() —
постоянная
Больцмана,
Т — температура,
—
постоянная
Больцмана,
Т — температура,
![]() —
температура Дебая.
—
температура Дебая.
Теплоёмкость при постоянном давлении для твёрдых тел незначительно отличается от теплоёмкости при постоянном объёме.
Петер Дебай построил теорию теплоёмкости твёрдого тела в 1912 году, усовершенствовав модель Эйнштейна, учитывая низкочастотные колебания кристаллической решётки — акустические фононы.
Фотон —
безмассовая нейтральная частица. Спин
фотона равен 1 (частица является бозоном),
но из-за нулевой массы покоя более
подходящей характеристикой является
спиральность,
проекция спина частицы на направление
движения. Фотон может находиться только
в двух спиновых состояниях со
спиральностью, равной
![]() .
Этому свойству в классической
электродинамике
соответствует поперечность электромагнитной
волны.[7]
.
Этому свойству в классической
электродинамике
соответствует поперечность электромагнитной
волны.[7]
Массу
покоя
фотона считают равной нулю, основываясь
на эксперименте и теоретических
обоснованиях, описанных выше. Поэтому
скорость фотона равна скорости
света.
По этой причине (не существует системы
отсчёта, в которой фотон покоится)
внутренняя
чётность
частицы не определена.[7]
Если приписать фотону наличие т. н.
«релятивистской
массы»
(термин ныне выходит из употребления)
исходя из соотношения
![]() то
она составит
то
она составит
![]() Фотон —
истинно
нейтральная частица
(тождественен своей античастице)[47],
поэтому его зарядовая
чётность
отрицательна и равна −1.
Фотон —
истинно
нейтральная частица
(тождественен своей античастице)[47],
поэтому его зарядовая
чётность
отрицательна и равна −1.
Фотон
относится к калибровочным
бозонам.
Он участвует в электромагнитном
и гравитационном
взаимодействии.[7]
Фотон не имеет электрического
заряда
и не распадается спонтанно в вакууме,
стабилен. Фотон может иметь одно из
двух состояний поляризации
и описывается тремя пространственными
параметрами — составляющими волнового
вектора,
который определяет его длину волны
![]() и
направление распространения.
и
направление распространения.
Фотоны излучаются во многих природных процессах, например, при движении электрического заряда с ускорением, при переходе атома или ядра из возбуждённого состояния в состояние с меньшей энергией, или при аннигиляции пары электрон-позитрон.[48] При обратных процессах — возбуждение атома, рождение электрон-позитронных пар — происходит поглощение фотонов.[49]
Если
энергия
фотона равна
,
то импульс
![]() связан
с энергией соотношением
связан
с энергией соотношением
![]() ,
где
—
скорость
света
(скорость, с которой в любой момент
времени движется фотон как безмассовая
частица). Для сравнения, для частиц с
ненулевой массой покоя связь массы и
импульса с энергией определяется
формулой
,
где
—
скорость
света
(скорость, с которой в любой момент
времени движется фотон как безмассовая
частица). Для сравнения, для частиц с
ненулевой массой покоя связь массы и
импульса с энергией определяется
формулой
![]() ,
как показано в специальной
теории относительности.[50]
,
как показано в специальной
теории относительности.[50]
В
вакууме энергия и импульс фотона зависят
только от его частоты
![]() (или,
что эквивалентно, от длины
волны
(или,
что эквивалентно, от длины
волны
![]() ):
):
![]() ,
,
![]() ,
,
и, следовательно, величина импульса есть:
![]() ,
,
где
—
постоянная
Планка,
равная
![]() ;
;
![]() —
волновой
вектор
и
—
волновой
вектор
и
![]() —
его величина (волновое
число);
—
его величина (волновое
число);
![]() —
угловая
частота.
Волновой вектор
указывает
направление движения фотона. Спин
фотона не зависит от частоты.
—
угловая
частота.
Волновой вектор
указывает
направление движения фотона. Спин
фотона не зависит от частоты.
Классические формулы для энергии и импульса электромагнитного излучения могут быть получены исходя из представлений о фотонах. К примеру, давление излучения осуществляется за счёт передачи импульса фотонов телу при их поглощении. Действительно, давление — это сила, действующая на единицу площади поверхности, а сила равна изменению импульса, отнесённому ко времени этого изменения.[51]
