13. Понятие сочетания. Теорема о числе сочетаний из n элементов по k. Свойства сочетаний.

Сочетанием из n элементов по m (иногда читают просто: из n по m) называется m-элементное подмножество некоторого n-элементного множества.   

Теорема. Число сочетаний из n элементов по k определяется по формуле:

= .

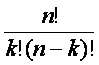Свойства сочетаний

Первое свойство непосредственно вытекает из формул:

Доказательство:

Составим -элементные сочетания из элементов и разобьем их на два класса:

1-й класс - сочетания, содержащие элемент ;

2-й класс - сочетания, не содержащие элемент .

Если из любого сочетания 1-го класса откинуть элемент , то останется сочетание из , их число .

Сочетания 2-го класса являются -элементными сочетаниями, составленными из , их число . Поскольку любое -элементное сочетание из принадлежит одному и только одному из этих классов, а общее число равно , то приходим к равенству

Доказательство:

- это число всех размещений с повторениями из элементов двух типов. Разобьем эти размещения на классы, отнеся в -й класс те, в которые входят элементов 1-го типа и элементов 2-го типа. Размещения k-го класса - это не что иное, как всевозможные перестановки из элементов 1-го типа и элементов 2-го типа. Мы знаем, что число таких перестановок равно

14. Понятие сочетания с повторениями. Теорема о числе сочетаний с повторениями.

Определение. Если каждому элементу некоторого конечного множества поставлено в соответствие целое неотрицательное число — кратность данного элемента, то говорят, что задано сочетание с повторениями. Сумма кратностей всех элементов называется порядком сочетания.

Всякое сочетание с повторениями -го порядка, составленное из множества, содержащего элементов, называется также сочетанием с повторением из элементов по .

Если — кратности элементов , то по определению есть порядок сочетания

Теорема. Число сочетаний с повторениями из элементов по выражается формулой

15. Понятие размещения. Теорема о числе размещений.

Определение. Размещениями множества из различных элементов по элементов называются комбинации, которые составлены из данных элементов по элементов и отличаются либо самими элементами, либо порядком элементов.

Число всех размещений множества из элементов по элементов обозначается через (от начальной буквы французского слова “arrangement”, что означает размещение), где и .

Теорема. Число размещений множества из элементов по элементов равно

Доказательство. Пусть у нас есть элементы . Пусть — возможные размещения. Будем строить эти размещения последовательно. Сначала определим — первый элемент размещения. Из данной совокупности элементов его можно выбрать различными способами. После выбора первого элемента для второго элемента остается способов выбора и т.д. Так как каждый такой выбор дает новое размещение, то все эти выборы можно свободно комбинировать между собой. Поэтому имеем: