1. Основные понятия теории множеств.

Понятие множества — является одним из тех фундаментальных понятий математики, которым трудно дать точное определение, используя элементарные понятия. Поэтому ограничимся описательным объяснением понятия множества.

Множеством называется совокупность определенных вполне различаемых объектов, рассматриваемых как единое целое. Создатель теории множеств Георг Кантор давал следующее определение множества — «множество есть многое, мыслимое нами как целое».

Отдельные объекты, из которых состоит множество, называются элементами множества.

Множества принято обозначать большими буквами латинского алфавита, а элементы этих множеств — маленькими буквами латинского алфавита. Множества записываются в фигурных скобках { }.

Принято использовать следующие обозначения:

a ∈ X — «элемент a принадлежит множеству X»;

a ∉ X — «элемент a не принадлежит множеству X»;

∀ — квантор произвольности, общности, обозначающий «любой», «какой бы не был», «для всех»;

∃ — квантор существования: ∃y ∈ B — «существует (найдется) элемент y из множества B»;

∃! — квантор существования и единственности: ∃!b ∈ C — «существует единственный элемент b из множества C»;

: — «такой, что; обладающий свойством»;

→ — символ следствия, означает «влечет за собой»;

⇔ — квантор эквивалентности, равносильности — «тогда и только тогда».

Множества бывают конечные и бесконечные. Множества называются конечным, если число его элементов конечно, т.е. если существует натуральное число n, являющееся числом элементов множества. А={a1, a2,a 3, ..., an}. Множество называется бесконечным, если оно содержит бесконечное число элементов. B={b1,b2,b3, ...}. Например, множество букв русского алфавита — конечное множество. Множество натуральных чисел — бесконечное множество.

Число элементов в конечном множестве M называется мощностью множества M и обозначается |M|. Пустоемножество — множество, не содержащее ни одного элемента — ∅. Два множества называются равными, если они состоят из одних и тех же элементов, т.е. представляют собой одно и тоже множество. Множества не равны X ≠ Y, если в Х есть элементы, не принадлежащие Y, или в Y есть элементы, не принадлежащие Х. Символ равенства множеств обладает свойствами:

Х=Х; — рефлексивность

если Х=Y, Y=X — симметричность

если X=Y,Y=Z, то X=Z — транзитивность.

Согласно такого определения равенства множеств мы естественно получаем, что все пустые множества равны между собой или что то же самое, что существует только одно пустое множество.

Понятие мультимножества.

Мультимножество — в математике, обобщение понятия множества, допускающее включение одного и того же элемента по нескольку раз

Число элементов в мультимножестве, с учетом повторяющихся элементов, называется его размером или мощностью.

Способы задания множеств.

Множество может быть задано перечислением всех его элементов или списком. В этом случае элементы множества записывают внутри фигурных скобок, например: А = { 1, 2, a, x } или B = { река Нил, город Москва, планета Уран}.

Множество может быть задано описанием свойств его элементов. Чаще всего при этом используют запись A = { x|P( x ) }, которую читают следующим образом: "A есть множество элементов x таких, что для них выполняется свойство P( x )".

Например, B = { x| x- натуральное число, меньшее 10 }, при этом, очевидно, B = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }.

Множество можно задать порождающей процедурой, например:

D = { z|1 О D,и если z О D,то z + 3 О D},

E = { x| x = 3k, k - любое нартуральное число.}

Наряду с порождающей процедурой существует распознающая или разрешающая процедура, которая позволяет определить, принадлежит ли данный объект множеству или нет. Для множества D распознающая процедура заключается в том, что для любого натурального числа n будут проверять, является ли число 3 делителем числа n - 1. Для множества E распознающая процедура заключается в разложении числа на простые множители.

Операции над множествами.

Множество A называется подмножеством множества B, если любой элемент множества A принадлежит множеству B. При этом пишут A М B, где " М " есть знак вложения подмножества. Из определения следует, что для любого множества A справедливы, как минимум, два вложения A М A и A М U.

В теории множеств, по определению, полагают, что пустое множество является подмножеством любого множества.

Пустое множество и само множество A называются несобственными подмножествами множества A.

При графическом изображении множеств удобно использовать диаграммы Венна , на которых универсальное множество обычно представляют в виде прямоугольника, а остальные множества в виде овалов, заключенных внутри этого прямоугольника (рис 1.1).

Объединением множеств A и B (обозначение A 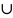B) называется множество элементов x таких, что x принадлежит хотя бы одному из двух множеств A или B (рис 1.2). Символически это можно записать следующим образом:

A B = {x|x 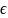A или x B}.

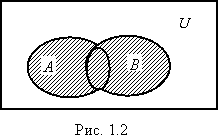
Пересечением множеств A и B (обозначение A B) называется множество, состоящее из элементов x, которые принадлежат и множеству A и множеству B (рис. 1.3):

A B = {x|x A и x B}.

Разностью множеств A и B называется множество всех тех элементов множества A, которые не принадлежат множеству B (рис. 1.4):

A\B = {x|x A и x B}.

Симметрической разностью множеств A и B называется множество A B = ( A\B ) ( B\A ) (рис. 1.5).

А бсолютным дополнением множества A называется множество всех элементов, не принадлежащих A, т.е. множество `A = U\A={x|x U и x А}., где U - универсальное множество (рис. 1.6).

Теорема о числе подмножеств n-элементного множества.

Число всех k-элементных подмножеств множества из n элементов равно