
- •1. Основные понятия теории множеств.
- •2. Понятие вектора.
- •3. Понятие соответствия между множествами.
- •4. Понятие отображения множеств.
- •5. Классификация множеств по мощности. Понятие счетного множества. Понятие несчётного множества.
- •6. Понятие отношения. Свойства отношений. Отношение эквивалентности, отношение строгого порядка, отношение нестрогого порядка.
- •7. Понятие операции, ассоциативной операции, дистрибутивной операции. Понятие алгебры, алгебраической системы, модели. Понятие группоида, полугруппы, коммутативной полугруппы.
- •8. Понятие группы. Группа подстановок.
- •9.Понятие кольца. Кольцо вычетов.
- •10. Определение поля
- •11. Перестановки
- •12.Перестановки с повторениями
- •13. Понятие сочетания. Теорема о числе сочетаний из n элементов по k. Свойства сочетаний.
- •Свойства сочетаний
- •14. Понятие сочетания с повторениями. Теорема о числе сочетаний с повторениями.
- •15. Понятие размещения. Теорема о числе размещений.
- •16. Понятие композиции. Теорема о числе композиций n.
- •18. Понятие композиции. Теорема о числе композиций n из k частей при рi0.
- •19. Основные понятия и определения теории графов.
- •20. Способы хранения графов в памяти эвм.
- •21. Алгоритм поиска на графах (поиск в глубину).
- •22. Алгоритм поиска на графах (поиск в ширину).
- •23. Понятие сильной связности. Анализ сильной связности с помощью алгоритмов поиска на графах.
- •25. Сильная связность. Отношение на вершинах графа называется отношением сильной связности. Сильная связность — отношение эквивалентности. Рассмотрим транзитивность:
- •26. Понятие логической функции. Способы задания логических функций.
- •27. Булева алгебра. Основные свойства операций булевой алгебры. Понятие двойственной и самодвойственной логической функции.
- •28. Алгебра Жегалкина. Основные свойства операций алгебры Жегалкина.
- •29. Алгебра Жегалкина. Представление логических функций полиномом Жегалкина.
- •33. Минимизация логических функций методом Квайна.
- •34. Понятие функционально-полной системы логических функций
- •35. 36 Понятие замкнутого класса. Класс монотонных логических функций.Понятие замкнутого класса. Класс линейный логических функций..
- •37. Теорема о функциональной полноте в слабом смысле.
- •38. Понятие замкнутого класса. Класс функций сохраняющих 0. Класс функций сохраняющих 1.
- •39. Понятие замкнутого класса. Класс самодвойственных функций.
- •40. Теорема о функциональной полноте.
29. Алгебра Жегалкина. Представление логических функций полиномом Жегалкина.
Определение. Полиномом Жегалкина для n логических переменных называется полином, являющийся суммой константы и различных одночленов, в которые все переменные входят не выше, чем в первой степени:
a
x![]() x
x![]() … x
… x![]() , ( 1 d k d n )
, ( 1 d k d n )
причем
в каждом наборе ( i![]() ,
, i
,
, i![]() ) все i
) все i![]() различны, а суммирование по mod 2 ведется
по некоторому множеству таких не
совпадающих наборов.
различны, а суммирование по mod 2 ведется
по некоторому множеству таких не
совпадающих наборов.
Например,
1
x
x
x![]() , x
x
x
, x
x
x![]() x
x
x
- некоторые полиномы Жегалкина для двух
и трех переменных соответственно.
x
x
x
- некоторые полиномы Жегалкина для двух
и трех переменных соответственно.
От формулы алгебры логики всегда можно перейти к формуле алгебры Жегалкина. Для этого нужно заменить основные элементарные функции алгебры логики на соответствующие эквивалентные выражения алгебры Жегалкина (1) - (5), представленные выше.
В полученной формуле нужно раскрыть скобки и произвести упрощения, используя соотношения (1.4), а также следующие соотношения: x & x = x и x·1 = x. Полученное выражение и будет полиномом Жегалкина для данной формулы.
Пример.
Найти полином Жегалкина для функции:
f( x, y ) = ( x
y
)(
![]() x
z ).
x
z ).
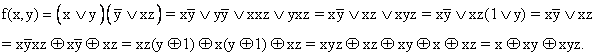
Полученное выражение и есть полином Жегалкина.
При нахождении полинома Жегалкина для некоторой формулы алгебры логики можно использовать следующее соотношение, вытекающее из представления дизъюнкции в алгебре Жегалкина:
f1 f2 = f1 f2, (1.5)
справедливое при f1f2 = 0. Используем соотношение (1.5) для нахождения полинома Жегалкина в следующих примерах.
Пример.
Найти полином Жегалкина для функции:
f( x, y ) = x y
![]() .
.
Сделаем следующие преобразования:
f(
x,y ) = x y
![]() =
x y
=
x y
(
x
1
)( y
1
) =
=
x y
=
x y
(
x
1
)( y
1
) =
= x y x y x y 1 = 1 x y - полиномом Жегалкина.
Пример. Найти полином Жегалкина для функции: f( x, y ) = x z.
Сделаем следующие преобразования:
f(
x,y ) = x
z
= x
![]() z
= x ( y
1
)
(
x
1
) z =
z
= x ( y
1
)
(
x
1
) z =
= x y x x z z = x z x y x z. - полиномом Жегалкина.
Теорема. Для любой логической функции существует полином Жегалкина и притом единственный.
Доказательство: Существование полинома доказано вышеприведенным алгоритмом получения полинома из логической формулы. Для доказательства единственности надо показать, что между множеством всех логических функций от n переменных и множеством всех полиномов Жегалкина от n переменных существует взаимно однозначное соответствие.
Полином Жегалкина можно найти методом неопределенных коэффициентов. Рассмотрим этот метод на следующим примере.
Пример. Найти полином Жегалкина для функции заданной векторно:
f( x,y ) = ( 0, 1, 1, 0 ).
Составим таблицу 1.14 задания данной функции.
Таблица 1.14
x |
y |
f |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Полином Жегалкина для функции двух переменных ищем в следующем виде:
f( x, y ) = a0 a1·x a2·y a3·xy (1.6)
Для определения коэффициентов полинома нужно подставить значения неизвестных и соответствующее значение функции в (1.6), согласно таблице 1.14.
Подставляя набор переменных(0,0) в (1.6) получим:
![]() .
.
![]() a
a![]() = 0.
= 0.
Аналогично
для набора (0,1) получим:
![]() .
a
= 1.
.
a
= 1.
Для
набора (1,0) получим:
![]() a
= 1.
a
= 1.
Для
набора (1,1) получим:
![]() a
= 0.
a
= 0.
Подставляя в (1.6) найденные значения коэффициентов получим искомый полином для данной функции:
f( x, y ) = x y.
Замечание.
Можно показать, что переменная
x![]() будет фиктивной
для некоторой функции тогда и только
тогда, когда полином Жегалкина для нее
не содержит переменной x
будет фиктивной
для некоторой функции тогда и только
тогда, когда полином Жегалкина для нее
не содержит переменной x
