
- •Вопрос 1
- •Вопрос 2
- •Вопрос 3
- •Применение дифференциала к приближенным вычислениям
- •3.Инвариантность формы первого дифференциала
- •Вопрос 4
- •Вопрос 5
- •Вопрос 6
- •Вопрос 7
- •Вопрос 8
- •Вопрос 9
- •Вопрос 10
- •Оценка точности вычисления определённого интеграла
- •Вопрос 11
- •Вопрос 14
- •Вопрос 15
- •Вопрос 16
- •Вопрос 17
- •Описание метода
- •Оценка погрешности
- •Вопрос 20
- •Вопрос 21
- •Вопрос 22
- •Сходимость степенных рядов
- •Признаки сходимости
- •Вопрос 23 Ряды Тейлора и Маклорена разложение основных элементарных функций
- •Вопрос 25
- •Можно доказать, что предел суммы, стоящий в правой части равенства равен интегралу
Применение дифференциала к приближенным вычислениям
Мы
установили, что дифференциал функции
является частью ее приращения и
отличается от нее на величину ![]() .
Эта величина при
.
Эта величина при ![]() является бесконечно
малой функцией более высокого порядка,
чем
является бесконечно
малой функцией более высокого порядка,
чем ![]() при
при ![]() ),
так как
),
так как![]() .Поэтому
при достаточно малых
.Поэтому
при достаточно малых ![]() имеет
место приближенное равенство
имеет
место приближенное равенство ![]() или
или ![]() ,
откуда
,
откуда![]() .(1)При
этом чем меньше
,
тем точнее значение функции.Равенство
(1) представляет собой "рабочую
формулу" применения дифференциала
к приближенным вычислениям.
.(1)При
этом чем меньше
,
тем точнее значение функции.Равенство
(1) представляет собой "рабочую
формулу" применения дифференциала
к приближенным вычислениям.
Пример.
Вычислите приближенно с двумя десятичными
знаками ![]() .
.
Решение.Введем
функцию ![]() и
в качестве x возьмем число,
наиболее близкое к
и
в качестве x возьмем число,
наиболее близкое к ![]() ,
но такое, чтобы
,
но такое, чтобы ![]() легко
вычислялся и
легко
вычислялся и ![]() было
бы достаточно малым. В нашем случае
удобно взять
было
бы достаточно малым. В нашем случае
удобно взять ![]() ,
тогда
,
тогда ![]() Найдем
Найдем ![]() .
.
Вычислим ![]() ,
, ![]() .
.
Тогда
по формуле (1)![]() .
.
Ответ: ![]() .
.
3.Инвариантность формы первого дифференциала
Если x - независимая переменная, то dx = x - x0 (фиксированное приращение). В этом случае имеем
df(x0) = f'(x0)dx. (3)
Если x = φ(t)
- дифференцируемая функция, то dx = φ'(t0)dt.
Следовательно,![]()
![]()
![]()
![]()
![]()
Вопрос 4
Производные высших порядков
явно заданной функции
Производная
у'=ƒ'(х) функции у=ƒ(х) есть также функция
от х и называется производной
первого порядка. Если
функция ƒ'(х) дифференцируема, то ее
производная называется производной
второго порядка и обозначается у"
![]()
![]() Итак,
у"=(у')'.
Производная
от производной второго порядка, если
она существует, называется производной
третьего порядка и
обозначается у'" (или ƒ'"(х)). Итак,
у'"=(y")' Производной n-го порядка
(или n-й производной) называется
производная от производной (n-1)
порядка: y(n)=(y(n-1))¢ .Производные
порядка выше первого называются
производными высших порядков.Начиная
с производной четвертого порядка,
производные обозначают римскими цифрами
или числами в скобках (уν или
у(5)—
производная пятого порядка).
Итак,
у"=(у')'.
Производная
от производной второго порядка, если
она существует, называется производной
третьего порядка и
обозначается у'" (или ƒ'"(х)). Итак,
у'"=(y")' Производной n-го порядка
(или n-й производной) называется
производная от производной (n-1)
порядка: y(n)=(y(n-1))¢ .Производные
порядка выше первого называются
производными высших порядков.Начиная
с производной четвертого порядка,
производные обозначают римскими цифрами
или числами в скобках (уν или
у(5)—
производная пятого порядка).
Пример:Найти производную 13-го порядка функции у=sinx.
Решение:
неявно заданной функции
Пусть функция у=ƒ(х) задана неявно в виде уравнения F(x;y)=0.
Продифференцировав это уравнение по х и разрешив полученное уравнение относительно у', найдем производную первого порядка (первую производную). Продифференцировав по х первую производную, получим вторую производую от неявной функции. В нее войдут х,у,у¢ . Подставляя уже найденное значение у' в выражение второй производной, выразим у" через х и у.
Аналогично поступаем для нахождения производной третьего (и дальше) порядка.
Пример: Найти у'", если х2+у2=1.
Решение:
Дифференцируем уравнение х2+у2-1=0
по х: 2х+2у· у¢ =0. Отсюда у'=-х/у. Далее
имеем:![]()
![]() (так
как х2+у2=1),
следовательно,
(так
как х2+у2=1),
следовательно,![]()
![]()
функций, заданных параметрически
Пусть
функция у=ƒ(х) задана параметрическими
уравнениями![]() Как
известно, первая производная у'х
находится по формуле (23.1)
Как
известно, первая производная у'х
находится по формуле (23.1)![]()
Найдем
вторую производную от функции заданной
параметрически. Из определения второй
производной и равенства (23.1) следует,
что![]()
![]() Аналогично
получаем
Аналогично
получаем
Пример 23.3
Найти вторую производную функции
![]()
Решение:
По формуле (23.1)![]() Тогда
по формуле (23.2)
Тогда
по формуле (23.2)![]()
Заметим,
что найти у"хх можно
по преобразованной формуле (23.2):![]()
Дифференциалы высших порядков
Для
функции, зависящей от одной
переменной z=f(x)
второй и третий дифференциалы выглядят
так:![]()
![]()
Отсюда
можно вывести общий вид дифференциала n-го
порядка от функции z=f(x) :![]()
При вычислении дифференциалов высших порядков очень важно, что dx есть произвольное и не зависящее от x , которое при дифференцировании по x следует рассматривать как постоянный множитель.
Для функции нескильких переменных
Если
функция z=f(x,
y)
имеет непрерывные частные производные
второго порядка, то дифференциал второго
порядка определяется так: ![]() .
.
![]()
![]()
![]()
![]()
Символически
общий вид дифференциала n-го
порядка от функции ![]() выглядит
следующим образом:
выглядит
следующим образом:
![]()
где ![]() а
а
![]() произвольные
приращения независимых
переменных
произвольные
приращения независимых
переменных ![]() .
Приращения
рассматриваются как постоянные и
остаются одними и теми же при переходе
от одного дифференциала к следующему.
Сложность выражения дифференциала
возрастает с увеличением числа
переменных.
.
Приращения
рассматриваются как постоянные и
остаются одними и теми же при переходе
от одного дифференциала к следующему.
Сложность выражения дифференциала
возрастает с увеличением числа
переменных.
Неинвариантность дифференциалов высших порядков
При n≥2 , n-й дифференциал не инвариантен (в отличие от инвариантности первого дифференциала), то есть выражение d nf зависит, вообще говоря, от того, рассматривается ли переменная x как независимая, либо как некоторая промежуточная функция другого переменного, например, x=φ(t).
Для доказательства неинвариантности дифференциалов высшего порядка достаточно привести пример. При n = 2 и y=f(x)=x3 :
если
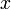 —
независимая переменная, то
—
независимая переменная, то 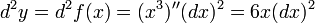
если
 и
и 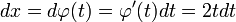

При,
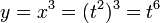 и
и 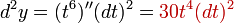
С учётом зависимости x=t2, уже второй дифференциал не обладает свойством инвариантности при замене переменной. Также не инвариантны дифференциалы порядков 3 и выше.
