
- •Вопрос 1
- •Вопрос 2
- •Вопрос 3
- •Применение дифференциала к приближенным вычислениям
- •3.Инвариантность формы первого дифференциала
- •Вопрос 4
- •Вопрос 5
- •Вопрос 6
- •Вопрос 7
- •Вопрос 8
- •Вопрос 9
- •Вопрос 10
- •Оценка точности вычисления определённого интеграла
- •Вопрос 11
- •Вопрос 14
- •Вопрос 15
- •Вопрос 16
- •Вопрос 17
- •Описание метода
- •Оценка погрешности
- •Вопрос 20
- •Вопрос 21
- •Вопрос 22
- •Сходимость степенных рядов
- •Признаки сходимости
- •Вопрос 23 Ряды Тейлора и Маклорена разложение основных элементарных функций
- •Вопрос 25
- •Можно доказать, что предел суммы, стоящий в правой части равенства равен интегралу
Вопрос 23 Ряды Тейлора и Маклорена разложение основных элементарных функций
Предположим,
что![]() в
интервале
в
интервале![]() есть
сумма степенного ряда (30.1):
есть
сумма степенного ряда (30.1):
(30.5)
![]()
Определим
коэфициенты![]() данного
ряда. Осуществим последовательное
дифференцирование тождества (30.5) и
используем в нем
данного
ряда. Осуществим последовательное
дифференцирование тождества (30.5) и
используем в нем![]()
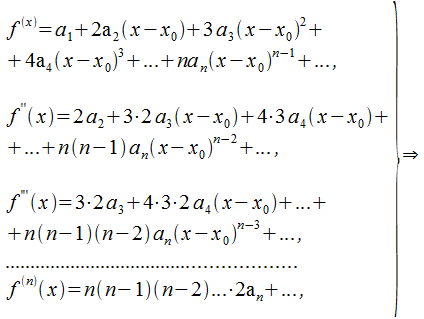

На основе этого находим коэффициенты:
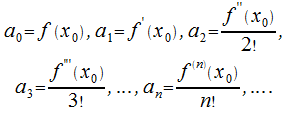
Используя их в (30.5), получим
(30.6)
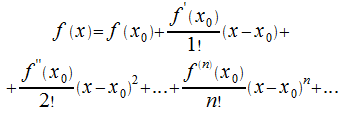
Обозначенный
ряд именуют рядом Тейлера для функции
,
а при![]() в
частном случае полученный ряд называется
рядом Маклорена:(30.7)
в
частном случае полученный ряд называется
рядом Маклорена:(30.7)
![]()
В
результате заключим: в случае, когда
функция
разлагается
по степеням
в
т.![]() является
бесконечно дифференцируемой.
является
бесконечно дифференцируемой.
Разложение функций в ряд Тейлора
Степенные
ряды.
Функциональный ряд ![]() ,
где
,
где ![]() -
числовая последовательность, называется
степенным рядом. Степенной ряд сходится
на интервале
-
числовая последовательность, называется
степенным рядом. Степенной ряд сходится
на интервале ![]() с
центром в точке
с
центром в точке ![]() .
Число R -
радиус сходимости степенного ряда
может быть вычислено по формулам
.
Число R -
радиус сходимости степенного ряда
может быть вычислено по формулам ![]() ,
или
,
или ![]() .
Степенной ряд сходится равномерно на
любом отрезке, целиком лежащем внутри
интервала сходимости. Сходимость
степенного ряда на границах интервала
сходимости необходимо исследовать
специально для конкретного ряда.
.
Степенной ряд сходится равномерно на
любом отрезке, целиком лежащем внутри
интервала сходимости. Сходимость
степенного ряда на границах интервала
сходимости необходимо исследовать
специально для конкретного ряда.
Разложение функций в ряд Тейлора. При исследовании свойств бесконечно дифференцируемых функций изучают их степенные ряды ряды Тейлора. Пусть функция f(x) определена в некоторой окрестности точки и имеет в этой точке производные всех порядков. Ряд
![]() называется
рядом Тейлора для функции f(x) в
точке
.
При
называется
рядом Тейлора для функции f(x) в
точке
.
При![]() такой
ряд называют также рядом Маклорена:
такой
ряд называют также рядом Маклорена:
![]() .
Функция f(x)может
быть разложена в степенной ряд на
интервале
,
если существует степенной ряд, сходящийся
к f(x)на
этом интервале. Если функция раскладывается
в степенной ряд в некоторой окрестности
точки
,
то это ряд Тейлора. Пусть
функция f(x)бесконечно
дифференцируема на интервале
и
все ее производные ограничены в
совокупности на этом интервале, то есть
существует число
.
Функция f(x)может
быть разложена в степенной ряд на
интервале
,
если существует степенной ряд, сходящийся
к f(x)на
этом интервале. Если функция раскладывается
в степенной ряд в некоторой окрестности
точки
,
то это ряд Тейлора. Пусть
функция f(x)бесконечно
дифференцируема на интервале
и
все ее производные ограничены в
совокупности на этом интервале, то есть
существует число ![]() ,
такое, что для всех
,
такое, что для всех ![]() и
для всех
и
для всех ![]() справедливо
неравенство
справедливо
неравенство ![]() .
Тогда ряд Тейлора сходится к f(x) для
всех
.
Тогда ряд Тейлора сходится к f(x) для
всех ![]() .
.
Приведем разложения в ряд Тейлора для основных элементарных функций.
![]()
![]()
![]()
![]()
![]()
![]()
Вопрос 25
ортогональные системы функций ряды Фурье.
Определение. Функции φ(х) и ψ (х), определенные на отрезке [a, b], называются ортогональными на этом отрезке, если
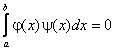
Определение. Последовательность функций φ1(x), φ2(x), …, φn(x), непрерывных на отрезке [a, b], называется ортогональной системой функций на этом отрезке, если все функции попарно ортогональны.
![]()
Отметим, что ортогональность функций не подразумевает перпендикулярности графиков этих функций.
Определение. Система функций называется ортогональной и нормированной (ортонормированной), если
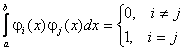
Определение. Рядом Фурье по ортогональной системе функций 1(x), 2(x), …,n(x) называется ряд вида:
![]()
коэффициенты которого определяются по формуле:
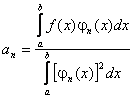 ,где f(x) =
-
сумма равномерно сходящегося на отрезке
[a, b]
ряда по ортогональной системе
функций. f(x)
– любая
функция, непрерывная или имеющая
конечное число точек разрыва первого
рода на отрезке [a, b].
,где f(x) =
-
сумма равномерно сходящегося на отрезке
[a, b]
ряда по ортогональной системе
функций. f(x)
– любая
функция, непрерывная или имеющая
конечное число точек разрыва первого
рода на отрезке [a, b].
В случае ортонормированной системы функций коэффициенты определяются:
![]()
Интеграл Фурье.
Пусть функция f(x) на каждом отрезке [-l,l], где l – любое число, кусочно – гладкая или кусочно – монотонная, кроме того, f(x) – абсолютно интегрируемая функция, т.е. сходится несобственный интеграл
![]()
Тогда функция f(x) разлагается в ряд Фурье:
![]()
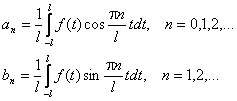
Если подставить коэффициенты в формулу для f(x), получим:
![]()
![]()
Переходя
к пределу при l,
можно доказать, что ![]() и
и
![]()
Обозначим ![]()
При l un 0.
![]()
