Вопрос 1

Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Пусть в некоторой окрестности точки x0R определена функция f: U(x0)R→R Производной функции называется такое число A, что функцию в окрестности U(x0) можно представить в виде f(x0+h) = f(x0)+Ah+o(h) если A существует. Определение производной функции через предел. Пусть в некоторой окрестности точки x0R определена функция U(x0)R→R  Производной функции f в точке x0 называется предел, если он существует,

Задачи, приводящие к понятию производной 

1. Задача о скорости движения. Рассмотрим уравнение неравномерного прямолинейного движения S=¦(t), определенного на множестве (a,b). Зафиксируем последовательно два момента времени t₀ и t ₁Î(a,b) и обозначим  D t =t₁ - t₀. Средней скоростью движения, соответствующей некоторому промежутку времени t, называется отношение пройденного пути, за этот промежуток времени Vср.=∆S/∆t (2-66) Средняя скорость не характеризует движение в каждый момент времени. Для того чтобы найти скорость в данный момент t₀, необходимо уменьшить промежуток времени t=t₁-t₀. Чем меньше промежуток, тем меньше средняя скорость отличается от скорости в данный момент времени, т. е. от мгновенной, точное значение скорости Vмгн. равно пределу ∆S/∆t  при , т. е. Vмгн. =lim_∆t→0∆S/∆t (2-67)

2. Задача о касательной. Пусть на множестве (a, b) задана функция y=¦(x). Отметили в декартовой ee системе координат XOY график в виде кривой К x₀; Возьмем две точки М₀ (¦(x₀)) и М₁(x₁;¦(x₁)) и проведем через них секущую М₀ М₁, ее угол наклона обозначим через a₁. Тогда, если точка М₁, двигаясь по кривой будет приближаться к точке М₀, положение секущей изменяется. 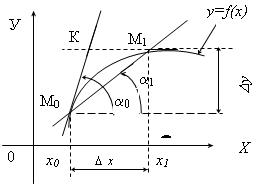Рис. 2.17. К задаче о секущей Когда точка М₁ совместиться с М₀, секущая превратиться в касательную. В этом случае lim_M1→M0 a₁=a₀, где a₀ - угол наклона касательной. Из рисунка видно, что tga1=CM1|/׀CM0| = (f(x1)- f(x0))/(x1-x0) (2-68) т.к. x₁-x₀=D x- это приращение аргумента, ¦(x₁)-¦(x₀)=D y - приращение функции, то tga₁= ∆y/∆x(2-69) Осуществляя предельный переход, когда М₁ М₀ lim_M1→M0 tga₁= tg lim _{Ф1→Ф0 ∆x→0} = tga₀. (2-70) Учитывая (2-69), имеем lim ∆y/∆x = tga₀ (2-71) Итак, тангенс угла наклона касательной tg a, равен пределу отношения приращения функции к приращению аргумента, когда последнее, равно нулю. Тангенс угла наклона касательной показывает, во сколько раз быстрее изменяется функция по сравнению с изменением аргумента в точке касания, т.е. характеризует скорость процесса или явления, описываемого кривой К. Зная тангенсы углов наклона касательной к графику функции в двух различных точках, можно сравнивать ’’крутизну подъема’’ графика. Так в точке (x₀,f(x₀)) (см. рис.) касательная расположена ''круто'', т. е. тангенс угла наклона большой, функция изменяется быстро, тогда как в точке (x₁,f(x₁)) тангенс угла наклона касательной мал, функция изменяется медленно. В точках, где касательная горизонта (tg =0), изменение функции почти не происходит. Если касательная к графику функции в некоторой точке ^ к оси OX, то функция изменяется с бесконечно большой скоростью.

Геометрический смысл производной.  Рассмотрим график функции  y = f ( x ): 

Из рис.1  видно, что для любых двух точек A и B графика функции: 

где  α - угол наклона секущей AB.

Таким образом, разностное отношение равно угловому коэффициенту секущей. Если зафиксировать точку A и двигать по направлению к ней точку B, то  ∆x неограниченно уменьшается и приближается к 0, а секущая АВ приближается к касательной АС. Следовательно, предел разностного отношения равен угловому коэффициенту касательной в точке A. Отсюда следует:производная функции в точке есть угловой коэффициент касательной к графику этой функции в этой точке.

Связь дифференцируемости с непрерывностью функции в точке. Если функция y=y(x) дифференцируема в точке x0, то она и непрерывна в этой точке. Справедливость утверждения следует из Δy=y/(x0)·Δx+α(Δx)·Δx и limΔx→0Δy=0, а по определению функция непрерывна, если малому приращению аргумента соответствует малое приращение функции.  Обратное утверждение не верно.  Например, функция y=∣x∣ непрерывна в точкеx=0, но не дифференцируема в этой точке.  Таким образом, не всякая непрерывная функция дифференцируема, а любая дифференцируемая функция непрерывна.

Если C — постоянное число и f=f(x), g=g(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

• C’=0

• X’=1

• (f+g)’=f’+g’

• (fg)’=f’g+fg’

• (Cf)’=Cf’

• (f/g)’=( f’g-fg’)/g² (g ≠ 0)

• (C/g)’= Cg’/g² (g ≠ 0)

• Если функция задана параметрически:

, то y_x’=dy/dx*dt/dx=y_t’*t_x’= y_t’/x_t’

• 

Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):

 где C^k_n — биномиальные коэффициенты.

Следующие свойства производной служат дополнением к правилам дифференцирования:

• если функция дифференцируема на интервале (a, b), то она непрерывна на интервале (a, b). Обратное, вообще говоря, неверно (например, функция y(x)=|x| на [-1, 1]);

• если функция имеет локальный максимум/минимум при значении аргумента, равном x, то f ’(x)=0 ;

• производная данной функции единственна, но у разных функций могут быть одинаковые производные.

• (f(x)^g(x))’=f(x)^g(x)[g’(x)*ln(f(x)) + (g(x)*f ’(x))/f(x)] (xD_f : f(x)>0)

Теорема о производной сложной функции

Пусть y(x)=f(u(x)) и существует f’(u) и u’(x), если существует конечный lim_∆u→0(∆f(u)/∆u)=f_u ’

По осн. теореме ∆f(u)/ ∆u= f_u ’+α(x) – бм

∆f(u) = f_u ’ ∆u +α(x) ∆u |*1/∆x

lim_∆x→0(∆f(u)/∆x)=f _x’= f _u’+ u _x’