
- •1.Кинематическое описание движения (ф-лы для описания поступательного и вращательного движения).
- •2. Современная трактовка законов Ньютона. Законы Ньютона
- •3.Постулаты специальной теории относительности и геометрия пространства - времени .
- •4. Фундаментальные взаимодействия
- •5.Силы тяготения и электрические силы
- •6.Напряженность поля сил. Принцип суперпозиции силовых полей
- •7.Магнитные силы. Сила Лоренца.
- •8. Силы упругости. Деформации, их виды.
- •9. Закон Гука и модуль Юнга.
- •10.Силы трения. Виды трения. Трение покоя. Внутреннее трение
- •12. Работа и кинетическая энергия. Мощность
- •13. Теорема живых сил. Закон сохранения полной механической энергии
- •14.Момент инерции твердого тела. Момент импульса. Теорема Штейнера
- •15.Уравнение движения и условия равновесия твердого тела
- •16.Закон сохранения момента импульса Кинетическая энергия вращения
- •17. Формула Ньютона для сил внутреннего трения. Коэффициент вязкости.
- •18. Гармонические колебания
- •19. Свободные затухающие колебания.
- •20.Вынужденные колебания осциллятора под действием синусоидальной силы
- •21. Амплитуда и фаза при вынужденных колебаниях. Резонансные кривые.
- •27. Точечный источник волн. Плоская и сферическая волна.
- •28. Фазовая скорость волны. Длина волны, волновое число.
- •29. Когерентность. Длина когерентности
- •30. Интерференция плоских волн условия возникновения интерференционного максимума и минимума.
- •31. Интерференция в тонких плёнках. Просветление оптики.
- •32. Принцип Гюйгенса-Френеля
- •33. Дифракция на круглом отверстии
- •36. Дифракция Фраунгофера и спектральное разложение. Разрешающая способность и дисперсия дифракционной решетки.
- •Модель атома Бора
- •Модели атома Томсона и Резерфорда
- •39. Гипотеза ДеБройля, свойства волн ДеБройля
- •41. Гипотеза Борна, волновая функция
- •42. Принцип неразличимости микрочастиц. Бозоны и фермионы
- •43. Квантование атома водорода. Квантовые числа
- •44. Характеристики квантовых чисел. Правила отбора.
- •45. Энергетическая диаграмма водородоподобного атома.
- •46. Вырождение энергетических уровней. Эффекты Зеемана и Штарка.
- •47.Спектры двухатомных молекул. Переходы в молекулярных спектрах.
- •48. Спектры твердого тела. Энергетические зоны.
- •49. Энергетические зоны и проводимость твердых тел.
- •55.Закон поглощения радиоактивного излучения
- •56.Способы регистрации радиоактивного излучения. Счетчик Гейгера и Камера Вильсона
- •57.Диэлектрики в электростатическом поле. Поляризация диэлектриков
- •58.Диэлектрическая проницаемость и диэлектрическая восприимчивость.
- •59.Теорема Остроградского-Гаусса. Ее использование для расчета полей симметричных объектов.
- •60. Конденсаторы. Электроемкость. Емкость плоского конденсатора и уединенной сферы
- •61. Электростатические поля в проводнике. Распределение потенциала и заряда по поверхности проводника
- •71. Три вида магнетиков. Их особенности.
- •75.Индуктивность соленоида. Взаимоиндукция. Принцип работы трансформатора.
- •76.Уравнения Максвелла, их физический смысл.
- •77.Электромагнитные волны. Их свойства. Соотношения Максвелла
- •78.Макроскопическая (термодинамическая) система. Интенсивные и экстенсивные переменные
- •79.Метод молекулярной динамики. Основное уравнение молекулярно-кинетической теории.
- •80. Уравнение Ван-дер-Вальса. Изотермы Ван-дер-Вальса. Уравнение Ван-дер-Вальса. Для одного моля газа Для молей газа
- •81. Критическая изотерма, закон соответственных состояний
- •83. Первое начало термодинамики. Обоснование
- •83. Первое начало термодинамики для изопроцессов
- •84. Основы теории теплоемкости. Формула Майера
- •96. Электрический ток в газах. Самостоятельный и несамостоятельный разряд
- •Виды газовых разрядов и их применение
21. Амплитуда и фаза при вынужденных колебаниях. Резонансные кривые.
Рассмотрим зависимость амплитуды А вынужденных колебаний от частоты .называя колеблющуюся величину либо смещением (х) колеблющегося тела из положения равновесия, либо зарядом (Q) конденсатора.
амплитуда А смещения (заряда) имеет максимум. Чтобы определить резонансную частоту рез, — частоту, при которой амплитуда А смещения (заряда) достигает максимума, — нужно найти максимум функции, или, что то же самое, минимум подкоренного выражения. Продифференцировав подкоренное выражение по и приравняв его нулю, получим условие, определяющее рез :
![]()
Это
равенство выполняется при =0, ±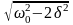 ,
у которых только лишь положительное
значение имеет физический смысл.
Следовательно, резонансная частота
,
у которых только лишь положительное
значение имеет физический смысл.
Следовательно, резонансная частота
![]() (148.1)
(148.1)
Явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы (частоты вынуждающего переменного напряжения) к частоте, равной или близкой собственной частоте колебательной системы, называется резонансом (соответственно механическим или электрическим). При значение рез практически совпадает с собственной частотой 0 колебательной системы. получим
![]()
![]() (148.2)
(148.2)
На
рис. 210 приведены зависимости амплитуды
вынужденных колебаний от частоты при
различных значениях .
Из (148.1) и (148.2) вытекает, что чем меньше
, тем выше и правее лежит максимум данной
кривой. Если 0, то все кривые достигают
одного в того же, отличного от нуля,
предельного значения
 ,
которое
называют статическим
отклонением.
В случае механических колебаний
,
которое
называют статическим
отклонением.
В случае механических колебаний
 ,
в случае электромагнитных – Um/(L
,
в случае электромагнитных – Um/(L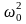 ).
Если , то вое кривые асимптотически
стремятся к нулю. Приведенная совокупность
кривых называется резонансными
кривыми.
).
Если , то вое кривые асимптотически
стремятся к нулю. Приведенная совокупность
кривых называется резонансными
кривыми.

Из формулы (148.2) вытекает, что при малом затухании ( ) резонансная амплитуда смещения (заряда)
![]()
где Q — добротность колебательной системы (см. (146.8)), — рассмотренное выше статическое отклонение. Отсюда следует, что добротность Q характеризует резонансные свойства колебательной системы: чем больше Q, тем больше Арез.
27. Точечный источник волн. Плоская и сферическая волна.
Точечный источник волн излучает когерентные волны (это волны, испускаемые источниками, имеющими одинаковую частоту и постоянную разность фаз)
К наиболее простым видам геометрических поверх-х относятся сфера и плоскость.
Сферическая волна
Волна называется сферической, если её волновые поверхности – сферы.
Плоская волна
Волна называется плоской, если её волновые поверхности – плоскости.
Плоская волна – одна из важнейших идеализаций волновой теории. Этой идеализацией можно воспользоваться, например, когда мы находимся на достаточно большом расстоянии от источника. Тогда в окрестности точки наблюдения можно пренебречь искривлением сферической волновой поверхности и считать волну приблизительно плоской.
28. Фазовая скорость волны. Длина волны, волновое число.
Фазовая скорость - скорость, с которой распространяется поверхность одинаковых фаз. В отсутствие дисперсии фазовая скорость волн не зависит от частоты. Поэтому, если есть набор волн разных частот, все они будут двигаться с одной и той же скоростью и пакет, который они образуют в результате сложения, при движении не изменяет своей первоначальной формы. Он движется с той же скоростью, что и волны, из которых состоит.
Связь
длины волны ![]() ,
фазовой скорости
,
фазовой скорости ![]() и
периода колебаний Т задается соотношением:
и
периода колебаний Т задается соотношением:
![]()

Длина
гармонической волны
 –
расстояние между двумя соседними
частицами, колеблющимися одинаковым
образом (в одинаковой фазе)
–
расстояние между двумя соседними
частицами, колеблющимися одинаковым
образом (в одинаковой фазе)
Волново́е
число́ —
это отношение 2π радиан
к длине волны: ![]()
В
 олновое
число является модулем волнового
вектора. Волновой
вектор
– это вектор, направление которого
совпадает с направлением распространения
бегущей волны.
олновое
число является модулем волнового
вектора. Волновой
вектор
– это вектор, направление которого
совпадает с направлением распространения
бегущей волны.
Единица измерения — рад·м−1,
