11. Отношение эквивалентности. Классы эквивалентности и их свойства. Разбиения множеств. Связь эквивалентности с разбиением (теоремы с доказательством).

Рефлексивное, симметричное и транзитивное отношение, заданное на множестве А, называется отношением эквивалентности на множестве А, т.е:

1.

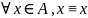
2. х,у

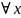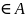3. ,y,z , х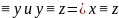

Классом эквивалентности [х], порожденным элементом х А, называется подмножество множества А, состоящее из тех и только тех элементов у, которые состоят в отношении эквивалентности с х, т.е. [х]={y: x=y, y }. Множество классов эквивалентности А\R называется фактор-множеством множества А по эквивалентности R: A\R={[x]:x A}.

Свойство классов эквивалентности:

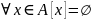1. . В самом деле х => х [x]

2. Класс эквивалентности порождается любым своим элементом, т.е. х 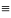у => [x]=[y]

   

3. Различные классы эквивалентности друг с другом не пересекаются, т.е. х у, то [х] [у]=

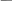
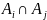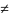Совокупность множеств А₁,А₂,…,А_n называется разбиением множества А, если выполняются два условия: А₁vA₂v…vA_n=A и = , i j, j=1..n.

Между разбиением множества и эквивалентностью, заданной на этом множестве существует связь, которая устанавливается следующими теоремами:

Теорема. Всякое отношение эквивалентности на множестве А определяет разбиение множества А, причем среди элементов разбиения нет пустых. Обратно, всякое разбиение на множестве А, не содержащее пустых элементов, определяет отношение эквивалентности на этом множестве.

Доказательство. Разбиение с непустыми элементами может быть построение по отношению к эквивалентности следующим образом:

1. Выбрать произвольный элемент а A

2. Построить класс эквивалентности [a]

3. A:=A\[a]; A:=A {[a]}

4. Если А непусто, перейти к шагу 1

5. Добавим класс Х в разбиение В:=В Х

6. Если U= , то разбиение построено, в противном случае переходим к шагу №2

12. Отношение порядка. Строгий и нестрогий порядок. Частичный и полный порядок. Упорядоченные множества.

Антисимметричное и транзитивное отношени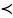е , заданное на множестве А, называется отношением порядка на множестве А, т.е.:

1. .

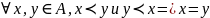2. .

Если ≺ - рефлексивно, то ≺ - нестрогий порядок.

Если ≺ - антирефлексивно, то ≺ - строгий порядок.

Если ≺ - связно, то ≺ - полный (линейный) порядок.

Если ≺ - несвязно, то ≺ - частичный порядок.

Например: Отношение на множестве чисел – строгий полный порядок, отношение - нестрогий полный порядок. Отношение с – строгий частичный порядок на булеане 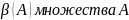. Схема организации подчинения – отношения строгого частичного порядка на множестве должностей.

Множество, на котором определено отношение частичного порядка, называется частично упорядоченным. Если на множестве определено отношение полного (линейного) порядка, то множество называется вполне упорядоченным (линейно упорядоченным). Например: числовое множество линейно упорядочено, а булеан упорядочен частично.

13. Соответствия. Образ и прообраз. Свойства соответствий: всюду определенные, инъективные, сюръективные, функциональные, взаимнооднозначные соответствия.

Соответствием между множествами А и В называется подмножество 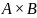. G – соответствие между А и В. Область определения соответствия: D_G={x: (x,y)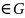 }. Область значений соответствия: Е_G={y: (x,y) G}.

Образом элемента а во множество В называется множество таких b B, (a,b) G. Образом множества С с А называется множество образов всех элементов С.

Прообразом элемента b B во множестве А, называется множество таких элементов а, что (а,b) G. Прообразом множества D c B называется множество прообразов всех элементов, принадлежащих D.

образ элемента а

а

В

А

b

образы

прообразы

Если G c A B, то говорят, что множеству А соответствует множество В. G:A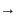 B. Пара множеств А и В определяет тип соответствия.

Свойства соответствий:

1. G называется всюду определенным в том и только в том случае, когда D_G=A

2. G называется сюръективным в том и только в том случае, когда Е_G=В

3. G называется функциональным (однозначным) в том и только в том случае, когда

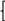
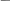
y₁=y₂

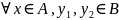: (x,y₁) G

(x,y₂) G

Каждому прообразу соответствует единственный образ

4. G называется инъективным в том и только том случае, когда

х₁=х₂

₁,х₂ А, у В: (x₁,y) G

(x₂,y) G

4. G называется биективным (взаимнооднозначным), если оно всюду определено, сюръективно,

функционально и инъективно.