
- •Множества. Элементы множеств. Интуитивный принцип объемности. Способы задания множества. Мощность множества.
- •Подмножества и их свойства.
- •Операции над множествами: объединение, пересечение, разность, дополнение. Диаграммы Эйлера-Венна.
- •Свойства операций над множествами (с доказательством).
- •Прямое произведение множеств. Бинарные отношения. Способы задания бинарных отношений.
- •Операции над бинарными отношениями: композиция отношений, степень отношения, обратное отношение, дополнение отношения, объединение, пересечение, разность отношений.
- •Свойства бинарных отношений: рефлексивность, антирефлексивность, симметричность, антисимметричность, транзитивность, связность.
- •Замыкания отношений. Транзитивное замыкание, рефлексивное транзитивное замыкание. Теоремы о транзитивном и рефлексивном транзитивном замыкании.
- •Операции над бинарными отношениями, заданными в матричной форме.
- •Алгоритм определения матрицы транзитивного замыкания бинарного отношения.
- •Отношение эквивалентности. Классы эквивалентности и их свойства. Разбиения множеств. Связь эквивалентности с разбиением (теоремы с доказательством).
- •Отношение порядка. Строгий и нестрогий порядок. Частичный и полный порядок. Упорядоченные множества.
- •Соответствия. Образ и прообраз. Свойства соответствий: всюду определенные, инъективные, сюръективные, функциональные, взаимнооднозначные соответствия.
- •Функции и отображения. Виды отображений. Обратные соответствия и функции. Способы задания функций.
- •Алгебраические операции. Примеры операций. Арность операции. Способы задания.
- •Свойства бинарных алгебраических операций: коммутативность, ассоциативность, дистрибутивность, поглощение, идемпотентность. Нейтральный и симметричный элементы.
- •Комбинаторные правила суммы и произведения. Выборки (упорядоченные, неупорядоченные, с повторениями и без).
- •Операции над графами.
- •Способы представления графов и орграфов на эвм: матрица смежности, матрица инцидентности, список смежности, массив ребер (дуг).
- •Маршруты в графах. Виды маршрутов: замкнутые и незамкнутые. Цепь. Простая цепь. Цикл. Простой цикл. Длина маршрута. Расстояние между вершинами. Диаметр графа.
- •Орграфы и бинарные отношения. Отношение достижимости вершин орграфа. Матрица достижимости. Связь между отношениями достижимости и смежности.
- •Определение матрицы достижимости орграфа как матрицы рефлексивного и транзитивного замыкания отношения смежности.
- •Алгоритм выделения компонент связности (сильной связности)
- •Нагруженные орграфы Длина пути в нагруженном орграфе. Минимальные пути в нагруженных орграфах.
- •Нагруженные орграфы. Алгоритм Форда-Беллмана выделения минимального пути в нагруженном орграфе.
Множества. Элементы множеств. Интуитивный принцип объемности. Способы задания множества. Мощность множества.
Множество – многое, мыслимое, как единое целое.
Состоит из объектов, но и само им является. Объекты из которых состоит множество – элементы.
Множества обычно обозначаются большими буквами: А, Х и т.д. Элементы же множеств, как правило, обозначают маленькими буквами: а, х и т.д. Для записи того, что а является элементом множества А применяется символ принадлежности.
Множество может содержать как конечное, так и бесконечное число элементов, соответственно, говорят, что множество конечно или бесконечно.
Интуитивный принцип объемности Г. Кантора (1 аксиома Геделя): множества А и В считаются равными (А = В), если они состоят из одних и тех же элементов.
Рассмотрим два основных способа задания неупорядоченных множеств:
- перечисление всех его элементов. В={1,2,3,…}
- описание характеристического (общего) свойства его элементов. А= {x: P(x)}. Здесь P(x) некоторое высказывание и множество А состоит только из тех x, для которых высказывание P(x) является верным.
Основные числовые множества:
N – натуральные числа
Z – целые числа
Q – рациональные числа
J – иррациональные числа
R – действительные числа (рациональные + иррациональные)
C – комплексные числа
Мощностью конечного множества А называется число его элементов. lАl-мощность.
Подмножества и их свойства.
Множество А называется подмножеством В, если любой элемент, принадлежащий А, принадлежит В.
АᴄВ<=>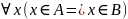 .
Если АᴄВ, то будем также говорить,
что множество А содержится в В, или
имеется включение А в В. Множества А и
В называются равными или совпадающими
(обозначается А=В), если они состоят из
одних и тех же элементов, т.е. если АᴄВ
и ВᴄА. Таким образом, чтобы доказать
равенство множеств, требуется установить
два включения.
.
Если АᴄВ, то будем также говорить,
что множество А содержится в В, или
имеется включение А в В. Множества А и
В называются равными или совпадающими
(обозначается А=В), если они состоят из
одних и тех же элементов, т.е. если АᴄВ
и ВᴄА. Таким образом, чтобы доказать
равенство множеств, требуется установить
два включения.
Свойства подмножеств:
 A,
AcA
A,
AcAA,
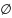 cA
cAA,B,C: { АᴄВ, BᴄC => A ᴄC - транзитивность
A,B: А=В
 { АᴄВ, ВᴄА
{ АᴄВ, ВᴄА
На свойстве 4 основано доказательство
равенства множеств А и В, т.е. для того
чтобы доказать, что А=В, нужно доказать
два включения АᴄВ(x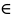 A,x
B),
ВᴄА(y
B,y
A).
Этот способ доказательства позволяет
проверить равенство множеств, не прибегая
к сравнению всех элементов, что актуально
для бесконечных множеств.
A,x
B),
ВᴄА(y
B,y
A).
Этот способ доказательства позволяет
проверить равенство множеств, не прибегая
к сравнению всех элементов, что актуально
для бесконечных множеств.
Операции над множествами: объединение, пересечение, разность, дополнение. Диаграммы Эйлера-Венна.
A
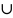 B
– множество состоящее из тех и только
тех элементов, которые принадлежат
одному из множеств А или В. A
B={x:
x
B
– множество состоящее из тех и только
тех элементов, которые принадлежат
одному из множеств А или В. A
B={x:
x }
}


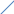

B
A
A
 B
– множество, состоящее из тех и только
тех элементов, которые принадлежат и
множеству А и множеству В. A
B={x:
x
B
– множество, состоящее из тех и только
тех элементов, которые принадлежат и
множеству А и множеству В. A
B={x:
x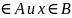 }
}
B
A




Разность множеств А\В={x: x }. А\В = В\А
B
A

4. U – универсальное множество (надмножество всех рассматриваемых в данном контексте
множеств).
B
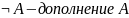 .
.
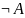 ={
x: x
={
x: x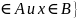
A









