6. Авторегрессионные модели. Автокорреляционная функция. Частная автокорреляционная функция.

Модель авторегрессии AR(p) порядка p имеет следующий вид:

, где 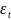- белый шум.

В общем случае такой временной ряд не будет стационарным, т.к. случайный член i скоррелирован со случайным членом j.

АКФ убывает экспоненциально, а ЧАКФ равна нулю начиная с момента p+1.

7. Модели скользящей средней. Автокорреляционная функция. Частная автокорреляционная функция.

Модель скользящей средней порядка q обозначается MA(q) и задаётся формулой z_t –  = а_t – ₁а_t – 1 –  – _qa_t – q.

Автокорреляции определяются формулами:

_k = 0 k > q

АКФ процесса MA(q) равна нулю для лагов, превышающих q. Память такого процесса ограничивается q шагами. Наблюдения, отстоящие более чем на q шагов, некоррелированы.

ЧАКФ такого процесса имеет бесконечную протяженность (с затуханием). ЧАКФ, как правило, представляет собой комбинацию затухающих экспонент и затухающих синусоидальных волн.

Пример для MA(1): ₁ = – /(1 + ²) и _k = 0 при k > 1. Частные автокорреляции определяются по формуле

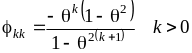
Выражения для частных автокорреляций процессов скользящей средней более высоких порядков получаются громоздкими, поэтому их здесь нет и не будет.

8. Модели arima. Автокорреляционная функция. Частная автокорреляционная функция.

Модель ARIMA – это модель авторегрессии и проинтегрированного скользящего среднего.

ARIMA(p,d,q), где p — параметры авторегрессии; d — порядок разностного оператора;
 q — параметры скользящего среднего, в своей основе имеет два процесса:

1. процесс авторегрессии:

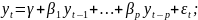
2. процесс скользящего среднего: 


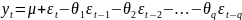
Нужно отметить, что 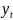- это ряд, получившийся из исходного путем построения разностей порядка d.

В общем виде ARIMA(p,d,q) имеет вид: 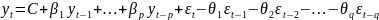. Не забываем при этом, что значения - это разности порядка d.

АКФ и ЧАКФ не убывают.

9. Метод главных компонент. Идеология. Вычисление главных компонент. Основные числовые характеристики главных компонент.

Метод главных компонент — один из основных способов уменьшить размерность данных, потеряв наименьшее количество информации. Пусть дан исходный набор векторов X линейного пространства L_k. Применение метода главных компонент позволяет перейти к базису пространства L_m (m≤k), такому что: первая компонента (первый вектор базиса) соответствует направлению, вдоль которого дисперсия векторов исходного набора максимальна. Направление второй компоненты (второго вектора базиса) выбрано таким образом, чтобы дисперсия исходных векторов вдоль него была максимальной при условии ортогональности первому вектору базиса. Аналогично определяются остальные векторы базиса. В результате, направления векторов базиса выбраны так, чтобы максимизировать дисперсию исходного набора вдоль первых компонент, называемых главными компонентами (или главными осями). Получается, что основная изменчивость векторов исходного набора векторов представлена несколькими первыми компонентами, и появляется возможность, отбросив оставшиеся (менее существенные) компоненты, перейти к пространству меньшей размерности.

Вычисление главных компонент

Пусть анализируемая случайная величина X имеет размерность p и матрицу ковариаци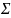й . Находятся все собственные значения этой матрицы λ₁, …, λ_p (для этого из диагональных значений матрицы ковариаций вычитаем λ, считаем определитель полученной матрицы, приравниваем его к нулю и решаем полученное уравнение относительно λ). Полученные собственные значения λ₁, …, λ_p ранжируются по убыванию их величины. После этого строятся собственные вектора, соответствующие этим собственным значениям: l₁, …, l_p. Далее, зная эти собственные вектора, составляем линейные комбинации с X, которые и будут являться главными компонентами.