Список вопросов по финансовой эконометрике

Сокращения:

АКФ – автокорреляционная функция

ЧАКФ – частная автокорреляционная функция

1. Белый шум. Автокорреляционная функция. Частная автокорреляционная функция. Тест Бокса-Льюнга. Белый шум

Белый шум - чисто случайный процесс, значения которого в различные моменты времени независимы и одинаково распределены (но не обязательно нормально распределены). Его определение выражается условиями:

E(y_t) = 

V(y_t) = ²

Таким образом, процесс белый шум имеет постоянную среднюю, постоянную дисперсию и нулевые автоковариации, за исключением случая нулевого лага.

Если процесс белого шума имеет нормальное распределение, то такой ряд называют гауссовским белым шумом.

АКФ для процесса белого шума равна нулю везде, кроме единственного пика с амплитудой 1 при r = 0.

ЧАКФ

Тест Бокса-Льюнга

Тест Бокса-Льюнга позволяет проверить гипотезу об отличии коэффициента автокорреляции от нуля.

Нулевая гипотеза H₀: данные являются случайными (т.е. представляют собой белый шум)

Альтернативная гипотеза H₁: данные не являются случайными

Рассчитывается Q-статистика: 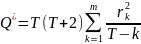, где T – объем выборки, m – максимальная длина лага, r_k – выборочный коэффициент автокорреляции для лага k.

Рассчитывается критическое значение статистики хи-квадрат: .

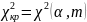Если 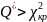, H₀ отвергается.

Если 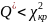, H₀ принимается при данном уровне значимости.

2. Построение модели локального тренда. Двойное экспоненциальное сглаживание. Критерий адекватности модели. Построение модели локального тренда

Модель локального линейного тренда имеет вид 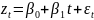. Построение данной модели является первым этапом приложения метода двойного экспоненциального сглаживания, так как полученные по методу наименьших квадратов оценки 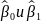необходимы для вычисления начальных значений сглаживающих статистик.

Двойное экспоненциальное сглаживание

Двойное экспоненциальное сглаживание – модель для прогнозирования временных рядов, имеющих линейный тренд. Называется также методом Брауна.

Вводятся сглаженные статистики первого и второго порядков:

Начальные значения сглаживающих статистик получаются по формулам:

;

;

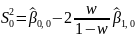где - оценки модели локального тренда по методу наименьших квадратов (см. первую часть этого вопроса).

Последующие значения сглаживающих статистик получаются рекуррентно.

Здесь w - дисконтирующий коэффицент, а 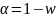- сглаживающая константа.

Оценки коэффициентов получаются по формулам:

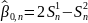
Прогноз на l шагов вперед рассчитывается следующим образом:

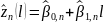
Обычно дисконтирующий коэффициент выбирается близким к 1. Дисконтирующий коэффициент w подбирается таким образом, чтобы SSE была минимальной.

Критерий адекватности модели

Чтобы проверить адекватность модели двойного экспоненциального сглаживания, следует рассчитать автокорреляции стандартных ошибок прогноза на один шаг вперед. Если ошибки прогноза некоррелированы, то двойное экспоненциальное сглаживание является адекватной моделью. Ошибки прогноза считаются некоррелированными тогда, когда все выборочные коэффициенты автокорреляции не отклоняются от нуля больше, чем на величину двух стандартных ошибок. (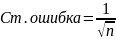 , где n – объем выборки).

3. Временные ряды. Ряды доходностей финансовых инструментов. Стационарные временные ряды. Определение стационарности в широком и узком смысле.

Временные ряды

Временным рядом называют последовательность наблюдений, упорядоченную во времени. Основной чертой, выделяющей анализ временных рядов среди других видов статистического анализа, является существенность порядка, в котором производятся наблюдения.

Ряды доходностей финансовых инструментов

Допустим, у нас имеется временной ряд цен P_i на определенные финансовые инструменты. Ряд доходностей получается из него по следующей формуле: .

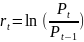Стационарные временные ряды. Определение стационарности в широком и узком смысле

Стационарность – свойство независимости процесса от времени.

В широком смысле условие стационарности означает, что средняя и дисперсия процесса постоянны, а автоковариации

_k = cov(z_t,z_t-k) = E(z_t – )E(z_t–k – )

и автокорреляции

зависят только от временного лага k.

В узком смысле стационарным называется такой стохастический процесс, распределение совместной вероятности которого не зависит от времени.